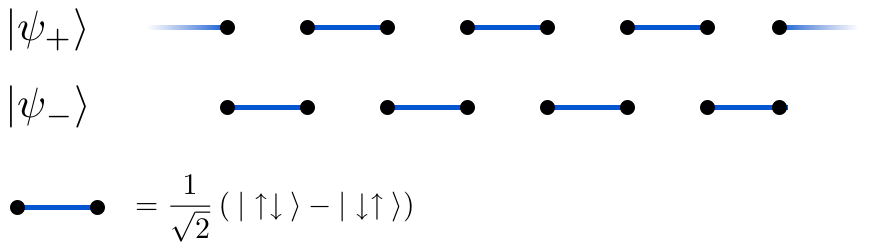Physics:Majumdar–Ghosh model

Short description: Quantum mechanical model with coupled spins

The Majumdar–Ghosh model is a one-dimensional quantum Heisenberg spin model in which the nearest-neighbour antiferromagnetic exchange interaction is twice as strong as the next-nearest-neighbour interaction. It is a special case of the more general [math]\displaystyle{ J_1 }[/math]-[math]\displaystyle{ J_2 }[/math] model, with [math]\displaystyle{ J_1=2J_2 }[/math]. The model is named after Indian physicists Chanchal Kumar Majumdar and Dipan Ghosh.

The Majumdar–Ghosh model is notable because its ground states (lowest energy quantum states) can be found exactly and written in a simple form, making it a useful starting point for understanding more complex spin models and phases.

Definition

The Majumdar–Ghosh model is defined by the following Hamiltonian:

[math]\displaystyle{ \hat H = J \sum_{j =1}^{N} \vec{S}_j \cdot \vec{S}_{j+1} + \frac{J}{2} \sum_{j =1}^{N} \vec{S}_j \cdot\vec{S}_{j+2} }[/math]

where the S vector is a quantum spin operator with quantum number S = 1/2.

Other conventions for the coefficients may be taken in the literature, but the most important fact is that the ratio of first-neighbor to second-neighbor couplings is 2 to 1. As a result of this ratio, it is possible to express the Hamiltonian (shifted by an overall constant) equivalently in the form

[math]\displaystyle{ \hat H = \frac{J}{4} \sum_{j =1}^{N} (\vec{S}_{j-1}+\vec{S}_j+ \vec{S}_{j+1})^2 }[/math]

The summed quantity is none other than the quadratic Casimir operator for representation of the spin algebra on the three consecutive sites [math]\displaystyle{ j-1, j, j+1 }[/math], which in turn can be decomposed into a direct sum of spin 1/2 and 3/2 representations. It has the eigenvalues [math]\displaystyle{ \frac{1}{2}(\frac{1}{2}+1) =3/4 }[/math] for the spin 1/2 subspace and [math]\displaystyle{ \frac{3}{2}(\frac{3}{2}+1) =15/4 }[/math] for the spin 3/2 subspace.

Ground states

It has been shown that the Majumdar–Ghosh model has two minimum energy states, or ground states, namely the states in which neighboring pairs of spins form singlet configurations. The wavefunction for each ground state is a product of these singlet pairs. This explains why there must be at least two ground states with the same energy, since one may be obtained from the other by merely shifting, or translating, the system by one lattice spacing. Furthermore, it has been shown that these (and linear combinations of them) are the unique ground states.

Generalizations

The Majumdar–Ghosh model is one of a small handful of realistic quantum spin models that may be solved exactly. Moreover, its ground states are simple examples of what are known as valence-bond solids (VBS). Thus the Majumdar–Ghosh model is related to another famous spin model, the AKLT model, whose ground state is the unique one dimensional spin one (S=1) valence-bond solid.

The Majumdar–Ghosh model is also a useful example of the Lieb–Schultz–Mattis theorem which roughly states that an infinite, one dimensional, half-odd-integer spin system must either have no energy spacing (or gap) between its ground and excited states or else have more than one ground state. The Majumdar–Ghosh model has a gap and falls under the second case.

The isotropy of the model is actually not important to the fact that it has an exactly dimerised ground state. For example, [math]\displaystyle{ \hat H = J \sum_{j =1}^{N} ({X}_j{X}_{j+1}+{Y}_j{Y}_{j+1} + \delta{Z}_j{Z}_{j+1}) + \frac{J}{2} \sum_{j =1}^{N} ({X}_j{X}_{j+2}+{Y}_j{Y}_{j+2} + \delta{Z}_j{Z}_{j+2}) }[/math] also has the same aforementioned exactly dimerised ground state for all real [math]\displaystyle{ \delta \gt -1/2 }[/math].

See also

• Heisenberg model (quantum)
• Heisenberg model (classical)
• J1 J2 model
• Bethe ansatz
• Ising model
• t-J model

References

• C K Majumdar and D Ghosh, On Next‐Nearest‐Neighbor Interaction in Linear Chain. J. Math. Phys. 10, 1388 (1969); doi:10.1063/1.1664978
• C K Majumdar, Antiferromagnetic model with known ground state. J. Phys. C: Solid State Phys. 3 911–915 (1970)
• Assa Auerbach, Interacting Electrons and Quantum Magnetism, Springer-Verlag New York (1992) p. 83