Physics:T-J model
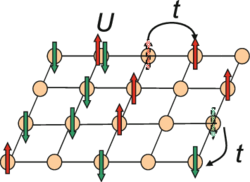
In solid-state physics, the t-J model is a model first derived in 1977 from the Hubbard model by Józef Spałek[1] to explain antiferromagnetic properties of the Mott insulators[2] and taking into account experimental results about the strength of electron-electron repulsion in this materials.[3] The model consider the materials as a lattice with atoms in the knots (sites) and just one or two external electrons moving among them (internal electrons are not considered), like in the basic Hubbard model. That difference is in supposing electrons being strongly-correlated, that means electrons are very sensible to reciprocal coulombic repulsion, and so are more constrained to avoid occupying lattice's sites already occupied by another electron. In the basic Hubbard model, the repulsion, indicated with U, can be small and also null, and electrons are freer to jump (hopping, parametrized by t as transfer or tunnel) from one site to another. In the t-J model, instead of U, there is the parameter J, function of the ratio t/U, so the name.
It is used as a possible model to explain high temperature superconductivity in doped antiferromagnets, in the hypothesis of strong coupling between electrons.[4][5]
The Hamiltonian
In quantum physics system's models are usually based on the Hamiltonian operator [math]\displaystyle{ \hat H }[/math], corresponding to the total energy of that system, including both kinetic energy and potential energy.
The t-J Hamiltonian can be derived from the [math]\displaystyle{ \hat H }[/math] of the Hubbard model using the Schrieffer–Wolff transformation, with the transformation generator depending on t/U and excluding the possibility for electrons to doubly occupy a lattice's site,[6] which results in:[7]
- [math]\displaystyle{ \hat H = -t\sum_{\langle ij\rangle,\sigma} \left( c_{i\sigma}^{\dagger} c_{j\sigma} + \mathrm{h.c.} \right) + J\sum_{\langle ij\rangle}\left(\mathbf{S}_{i}\cdot \mathbf{S}_{j}-\frac{n_in_j}{4}\right) + O(t^3/U^2) }[/math]
where the term in t corresponds to the kinetic energy and is equal to the one in the Hubbard model. The second one is the potential energy approximated at the second order, because this is an approximation of the Hubbard model in the limit U >> t developed in power of t. Terms at higher order can be added.[1]
The parameters are:
- is the sum over nearest-neighbor sites i and j, for all sites, typically on a two-dimensional square lattice,
- c†iσ, ciσ are the fermionic creation and annihilation operators at site i,
- σ is the spin polarization,
- t is the hopping integral,
- J is the antiferromagnetic exchange coupling, J = 4t2/U,
- U is the on-site coulombic repulsion, that must satisfy the condition for U >> t,
- ni = c†iσciσ is the particle number at site i and can be maximum 1, so that double occupancy is forbidden (in the Hubbard model is possible),
- Si and Sj are the spins on sites i and j,
- h. c. stands for Hermitian conjugate,
If ni = 1, that is when in the ground state, there is just one electron per lattice's site (half-filling), the model reduces to the Heisenberg model and the ground state reproduce a dielectric antiferromagnets (Mott insulator).[8]
The model can be further extended considering also the next-nearest-neighbor sites and the chemical potential to set the ground state in function of the total number of particles:[9][10]
- [math]\displaystyle{ \mathcal{\hat H} = t_1 \sum\limits_{\langle i,j \rangle} \left( c_{i\sigma}^{\dagger} c_{j\sigma} + \mathrm{h.c.} \right) \ + \ t_2 \sum\limits_{\langle\langle i,j \rangle\rangle} \left( c_{i\sigma}^{\dagger} c_{j\sigma} + \mathrm{h.c.} \right) \ + \ J \sum\limits_{\langle i,j \rangle} \left( \mathbf{S}_{i} \cdot \mathbf{S}_{j} - \frac{ n_{i} n_{j} }{4}\right) - \ \mu\sum\limits_{i} n_{i} , }[/math]
where ⟨...⟩ and ⟨⟨...⟩⟩ denote the nearest and next-nearest neighbors, respectively, with two different values for the hopping integral (t1 and t2) and μ is the chemical potential.
References
- ↑ 1.0 1.1 Chao, K. A.; Spałek, J.; Oleś, A. M. (1978-10-01). "Canonical perturbation expansion of the Hubbard model". Physical Review B 18 (7): 3453–3464. doi:10.1103/PhysRevB.18.3453. Bibcode: 1978PhRvB..18.3453C. https://link.aps.org/doi/10.1103/PhysRevB.18.3453.
- ↑ Anderson, P. W. (1959-07-01). "New Approach to the Theory of Superexchange Interactions". Physical Review 115 (1): 2–13. doi:10.1103/PhysRev.115.2. Bibcode: 1959PhRv..115....2A. https://link.aps.org/doi/10.1103/PhysRev.115.2.
- ↑ Nagaoka, Yosuke (1966-07-08). "Ferromagnetism in a Narrow, Almost Half-Filled s Band". Physical Review 147 (1): 392–405. doi:10.1103/PhysRev.147.392. Bibcode: 1966PhRv..147..392N. https://link.aps.org/doi/10.1103/PhysRev.147.392.
- ↑ Spalek, Jozef (2007-06-28). "t-J model then and now: A personal perspective from the pioneering times". Acta Physica Polonica A 111 (4): 409. doi:10.12693/APhysPolA.111.409. Bibcode: 2007AcPPA.111..409S.
- ↑ Rømer, Astrid T.; Maier, Thomas A.; Kreisel, Andreas; Eremin, Ilya; Hirschfeld, P. J.; Andersen, Brian M. (2020-01-31). "Pairing in the two-dimensional Hubbard model from weak to strong coupling". Physical Review Research 2 (1): 013108. doi:10.1103/PhysRevResearch.2.013108. Bibcode: 2020PhRvR...2a3108R. https://link.aps.org/doi/10.1103/PhysRevResearch.2.013108.
- ↑ This is done using a projector quantum operator [math]\displaystyle{ \hat P }[/math] that project [math]\displaystyle{ \hat H_t }[/math] on the subspace where fermionic operators can not add an electron on a site already occupied (see next note)
- ↑ Eckle, Hans-Peter (2019). "8.8.1 From the Hubbard to the t–J model: non-half filled band case". Models of Quantum Matter. Oxford University Press. ISBN 9780199678839. http://physics.gu.se/~tfkhj/HubbardEckle.pdf.
- ↑ Izyumov, Yu. A.; Chashchin, N. I. (1998). "tJ -model in terms of equations with variational derivatives". Condensed Matter Physics 1 (1): 41–56. doi:10.5488/CMP.1.1.41. Bibcode: 1998CMPh....1...41I.
- ↑ Karchev, Naoum (1998). "Generalized CP1 model from the t1-t2-J model". Phys. Rev. B 57 (17): 10913. doi:10.1103/PhysRevB.57.10913. Bibcode: 1998PhRvB..5710913K.
- ↑ Yanagisawa, Takashi (2008-02-12). "Phase diagram of thet–U2Hamiltonian of the weak coupling Hubbard model" (in en). New Journal of Physics 10 (2): 023014. doi:10.1088/1367-2630/10/2/023014. ISSN 1367-2630. Bibcode: 2008NJPh...10b3014Y. https://iopscience.iop.org/article/10.1088/1367-2630/10/2/023014.
Further reading
- Fazekas, Patrik (1999) (in EN). Lectures on Correlation and Magnetism. Series in Modern Condensed Matter Physics: Volume 5. 5. World Scientific. p. 199. doi:10.1142/2945. ISBN 978-981-4499-62-0.
- Spałek, Józef (2007). "t-J model then and now: A personal perspective from the pioneering times". Acta Phys. Pol. A 111 (4): 409–424. doi:10.12693/APhysPolA.111.409. Bibcode: 2007AcPPA.111..409S.
- Dr Mitchell (in en), Electron interactions and the Hubbard model, https://www.youtube.com/watch?v=wtYQlELm3tk, retrieved 2022-08-29
 |  |
