Physics:Mindlin–Reissner plate theory

Deformation of a plate highlighting the displacement, the mid-surface (red) and the normal to the mid-surface (blue)

The Uflyand-Mindlin theory of vibrating plates is an extension of Kirchhoff–Love plate theory that takes into account shear deformations through-the-thickness of a plate. The theory was proposed in 1948 by Yakov Solomonovich Uflyand (1916-1991) and in 1951 by Raymond Mindlin with Mindlin making reference to Uflyand's work. Hence, this theory has to be referred to as Uflyand-Mindlin plate theory, as is done in the handbook by Elishakoff, and in papers by Andronov, Elishakoff, Hache and Challamel, Loktev, Rossikhin and Shitikova and Wojnar. In 1994, Elishakoff suggested to neglect the fourth-order time derivative in Uflyand-Mindlin equations. A similar, but not identical, theory in static setting, had been proposed earlier by Eric Reissner in 1945. Both theories are intended for thick plates in which the normal to the mid-surface remains straight but not necessarily perpendicular to the mid-surface. The Uflyand-Mindlin theory is used to calculate the deformations and stresses in a plate whose thickness is of the order of one tenth the planar dimensions while the Kirchhoff–Love theory is applicable to thinner plates.

The form of Uflyand-Mindlin plate theory that is most commonly used is actually due to Mindlin. The Reissner theory is slightly different and is a static counterpart of the Uflyand-Mindlin theory. Both theories include in-plane shear strains and both are extensions of Kirchhoff–Love plate theory incorporating first-order shear effects.

Uflyand-Mindlin's theory assumes that there is a linear variation of displacement across the plate thickness but that the plate thickness does not change during deformation. An additional assumption is that the normal stress through the thickness is ignored; an assumption which is also called the plane stress condition. On the other hand, Reissner's static theory assumes that the bending stress is linear while the shear stress is quadratic through the thickness of the plate. This leads to a situation where the displacement through-the-thickness is not necessarily linear and where the plate thickness may change during deformation. Therefore, Reissner's static theory does not invoke the plane stress condition.

The Uflyand-Mindlin theory is often called the first-order shear deformation theory of plates. Since a first-order shear deformation theory implies a linear displacement variation through the thickness, it is incompatible with Reissner's static plate theory.

Mindlin theory

Mindlin's theory was originally derived for isotropic plates using equilibrium considerations by Uflyand. A more general version of the theory based on energy considerations is discussed here.

Assumed displacement field

The Mindlin hypothesis implies that the displacements in the plate have the form

[math]\displaystyle{ \begin{align} u_\alpha(\mathbf{x}) & = u^0_\alpha(x_1,x_2) - x_3~\varphi_\alpha ~;~~\alpha=1,2 \\ u_3(\mathbf{x}) & = w^0(x_1, x_2) \end{align} }[/math]

where [math]\displaystyle{ x_1 }[/math] and [math]\displaystyle{ x_2 }[/math] are the Cartesian coordinates on the mid-surface of the undeformed plate and [math]\displaystyle{ x_3 }[/math] is the coordinate for the thickness direction, [math]\displaystyle{ u^0_\alpha,~ \alpha=1,2 }[/math] are the in-plane displacements of the mid-surface, [math]\displaystyle{ w^0 }[/math] is the displacement of the mid-surface in the [math]\displaystyle{ x_3 }[/math] direction, [math]\displaystyle{ \varphi_1 }[/math] and [math]\displaystyle{ \varphi_2 }[/math] designate the angles which the normal to the mid-surface makes with the [math]\displaystyle{ x_3 }[/math] axis. Unlike Kirchhoff–Love plate theory where [math]\displaystyle{ \varphi_\alpha }[/math] are directly related to [math]\displaystyle{ w^0 }[/math], Mindlin's theory does not require that [math]\displaystyle{ \varphi_1 = w^0_{,1} }[/math] and [math]\displaystyle{ \varphi_2 = w^0_{,2} }[/math].

Displacement of the mid-surface (left) and of a normal (right)

Strain-displacement relations

Depending on the amount of rotation of the plate normals two different approximations for the strains can be derived from the basic kinematic assumptions.

For small strains and small rotations the strain–displacement relations for Mindlin–Reissner plates are

[math]\displaystyle{ \begin{align} \varepsilon_{\alpha\beta} & = \frac{1}{2}(u^0_{\alpha,\beta}+u^0_{\beta,\alpha}) - \frac{x_3}{2}~(\varphi_{\alpha,\beta}+\varphi_{\beta,\alpha}) \\ \varepsilon_{\alpha 3} & = \cfrac{1}{2}\left(w^0_{,\alpha}- \varphi_\alpha\right) \\ \varepsilon_{33} & = 0 \end{align} }[/math]

The shear strain, and hence the shear stress, across the thickness of the plate is not neglected in this theory. However, the shear strain is constant across the thickness of the plate. This cannot be accurate since the shear stress is known to be parabolic even for simple plate geometries. To account for the inaccuracy in the shear strain, a shear correction factor ([math]\displaystyle{ \kappa }[/math]) is applied so that the correct amount of internal energy is predicted by the theory. Then

[math]\displaystyle{ \varepsilon_{\alpha 3} = \cfrac{1}{2}~\kappa~\left(w^0_{,\alpha}- \varphi_\alpha\right) }[/math]

Equilibrium equations

The equilibrium equations of a Mindlin–Reissner plate for small strains and small rotations have the form

[math]\displaystyle{ \begin{align} & N_{\alpha\beta,\alpha} = 0 \\ & M_{\alpha\beta,\beta}-Q_\alpha = 0 \\ & Q_{\alpha,\alpha}+q = 0 \end{align} }[/math]

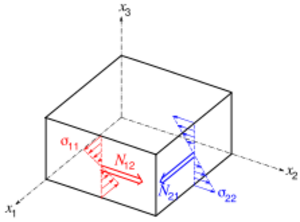
where [math]\displaystyle{ q }[/math] is an applied out-of-plane load, the in-plane stress resultants are defined as

[math]\displaystyle{ N_{\alpha\beta} := \int_{-h}^h \sigma_{\alpha\beta}~dx_3 \,, }[/math]

the moment resultants are defined as

[math]\displaystyle{ M_{\alpha\beta} := \int_{-h}^h x_3~\sigma_{\alpha\beta}~dx_3 \,, }[/math]

and the shear resultants are defined as

[math]\displaystyle{ Q_\alpha := \kappa~\int_{-h}^h \sigma_{\alpha 3}~dx_3 \,. }[/math]

Derivation of equilibrium equations

For the situation where the strains and rotations of the plate are small the virtual internal energy is given by [math]\displaystyle{ \begin{align} \delta U & = \int_{\Omega^0} \int_{-h}^h \boldsymbol{\sigma}:\delta\boldsymbol{\epsilon}~dx_3~d\Omega = \int_{\Omega^0} \int_{-h}^h \left[\sigma_{\alpha\beta}~\delta\varepsilon_{\alpha\beta} + 2~\sigma_{\alpha 3}~\delta\varepsilon_{\alpha 3}\right]~dx_3~d\Omega \\ & = \int_{\Omega^0} \int_{-h}^h \left[\frac{1}{2}~\sigma_{\alpha\beta}~(\delta u^0_{\alpha,\beta}+\delta u^0_{\beta,\alpha}) - \frac{x_3}{2}~\sigma_{\alpha\beta}~(\delta \varphi_{\alpha,\beta}+\delta\varphi_{\beta,\alpha}) + \kappa~\sigma_{\alpha 3}\left(\delta w^0_{,\alpha} - \delta \varphi_\alpha\right)\right]~dx_3~d\Omega \\ & = \int_{\Omega^0} \left[\frac{1}{2}~N_{\alpha\beta}~(\delta u^0_{\alpha,\beta}+\delta u^0_{\beta,\alpha}) - \frac{1}{2}M_{\alpha\beta}~(\delta \varphi_{\alpha,\beta}+\delta\varphi_{\beta,\alpha}) + Q_\alpha\left(\delta w^0_{,\alpha} - \delta \varphi_\alpha\right)\right]~d\Omega \end{align} }[/math] where the stress resultants and stress moment resultants are defined in a way similar to that for Kirchhoff plates. The shear resultant is defined as [math]\displaystyle{ Q_\alpha := \kappa~\int_{-h}^h \sigma_{\alpha 3}~dx_3 }[/math] Integration by parts gives [math]\displaystyle{ \begin{align} \delta U & = \int_{\Omega^0} \left[-\frac{1}{2}~(N_{\alpha\beta,\beta}~\delta u^0_{\alpha}+N_{\alpha\beta,\alpha}~\delta u^0_{\beta}) + \frac{1}{2}(M_{\alpha\beta,\beta}~\delta \varphi_{\alpha}+M_{\alpha\beta,\alpha}\delta\varphi_{\beta}) - Q_{\alpha,\alpha}~\delta w^0 - Q_\alpha~\delta\varphi_\alpha\right]~d\Omega \\ & + \int_{\Gamma^0} \left[\frac{1}{2}~(n_\beta~N_{\alpha\beta}~\delta u^0_\alpha+n_\alpha~N_{\alpha\beta}~\delta u^0_{\beta}) - \frac{1}{2}(n_\beta~M_{\alpha\beta}~\delta \varphi_{\alpha}+n_\alpha M_{\alpha\beta}\delta\varphi_\beta) + n_\alpha~Q_\alpha~\delta w^0\right]~d\Gamma \end{align} }[/math] The symmetry of the stress tensor implies that [math]\displaystyle{ N_{\alpha\beta} = N_{\beta\alpha} }[/math] and [math]\displaystyle{ M_{\alpha\beta} = M_{\beta\alpha} }[/math]. Hence, [math]\displaystyle{ \begin{align} \delta U & = \int_{\Omega^0} \left[-N_{\alpha\beta,\alpha}~\delta u^0_{\beta} + \left(M_{\alpha\beta,\beta}-Q_\alpha\right)~\delta \varphi_{\alpha} - Q_{\alpha,\alpha}~\delta w^0\right]~d\Omega \\ & + \int_{\Gamma^0} \left[n_\alpha~N_{\alpha\beta}~\delta u^0_{\beta} - n_\beta~M_{\alpha\beta}~\delta \varphi_{\alpha} + n_\alpha~Q_\alpha~\delta w^0\right]~d\Gamma \end{align} }[/math] For the special case when the top surface of the plate is loaded by a force per unit area [math]\displaystyle{ q(\mathbf{x}^0) }[/math], the virtual work done by the external forces is [math]\displaystyle{ \delta V_{\mathrm{ext}} = \int_{\Omega^0} q~\delta w^0~\mathrm{d}\Omega }[/math] Then, from the principle of virtual work, [math]\displaystyle{ \begin{align} & \int_{\Omega^0} \left[N_{\alpha\beta,\alpha}~\delta u^0_{\beta} - \left(M_{\alpha\beta,\beta}-Q_\alpha\right)~\delta \varphi_{\alpha} + \left(Q_{\alpha,\alpha}+q\right)~\delta w^0 \right]~d\Omega \\ & \qquad \qquad = \int_{\Gamma^0} \left[n_\alpha~N_{\alpha\beta}~\delta u^0_{\beta} - n_\beta~M_{\alpha\beta}~\delta \varphi_{\alpha} + n_\alpha~Q_\alpha~\delta w^0\right]~d\Gamma \end{align} }[/math] Using standard arguments from the calculus of variations, the equilibrium equations for a Mindlin–Reissner plate are [math]\displaystyle{ \begin{align} & N_{\alpha\beta,\alpha} = 0 \\ & M_{\alpha\beta,\beta}-Q_\alpha = 0 \\ & Q_{\alpha,\alpha}+q = 0 \end{align} }[/math]

Bending moments and normal stresses

Torques and shear stresses

Shear resultant and shear stresses

Boundary conditions

The boundary conditions are indicated by the boundary terms in the principle of virtual work.

If the only external force is a vertical force on the top surface of the plate, the boundary conditions are

[math]\displaystyle{ \begin{align} n_\alpha~N_{\alpha\beta} & \quad \mathrm{or} \quad u^0_\beta \\ n_\alpha~M_{\alpha\beta} & \quad \mathrm{or} \quad \varphi_\alpha \\ n_\alpha~Q_\alpha & \quad \mathrm{or} \quad w^0 \end{align} }[/math]

Stress–strain relations

The stress–strain relations for a linear elastic Mindlin–Reissner plate are given by

[math]\displaystyle{ \begin{align} \sigma_{\alpha\beta} & = C_{\alpha\beta\gamma\theta}~\varepsilon_{\gamma\theta} \\ \sigma_{\alpha 3} & = C_{\alpha 3\gamma\theta}~\varepsilon_{\gamma\theta} \\ \sigma_{33} & = C_{33\gamma\theta}~\varepsilon_{\gamma\theta} \end{align} }[/math]

Since [math]\displaystyle{ \sigma_{33} }[/math] does not appear in the equilibrium equations it is implicitly assumed that it does not have any effect on the momentum balance and is neglected. This assumption is also called the plane stress assumption. The remaining stress–strain relations for an orthotropic material, in matrix form, can be written as

[math]\displaystyle{ \begin{bmatrix}\sigma_{11} \\ \sigma_{22} \\ \sigma_{23} \\ \sigma_{31} \\ \sigma_{12} \end{bmatrix} = \begin{bmatrix} C_{11} & C_{12} & 0 & 0 & 0 \\ C_{12} & C_{22} & 0 & 0 & 0 \\ 0 & 0 & C_{44} & 0 & 0 \\ 0 & 0 & 0 & C_{55} & 0 \\ 0 & 0 & 0 & 0 & C_{66}\end{bmatrix} \begin{bmatrix}\varepsilon_{11} \\ \varepsilon_{22} \\ \varepsilon_{23} \\ \varepsilon_{31} \\\varepsilon_{12}\end{bmatrix} }[/math]

Then

[math]\displaystyle{ \begin{align} \begin{bmatrix}N_{11} \\ N_{22} \\ N_{12} \end{bmatrix} & = \int_{-h}^h \begin{bmatrix} C_{11} & C_{12} & 0 \\ C_{12} & C_{22} & 0 \\ 0 & 0 & C_{66} \end{bmatrix} \begin{bmatrix}\varepsilon_{11} \\ \varepsilon_{22} \\ \varepsilon_{12} \end{bmatrix} dx_3 \\[5pt] & = \left\{ \int_{-h}^h \begin{bmatrix} C_{11} & C_{12} & 0 \\ C_{12} & C_{22} & 0 \\ 0 & 0 & C_{66} \end{bmatrix}~dx_3 \right\} \begin{bmatrix} u^0_{1,1} \\ u^0_{2,2} \\ \frac{1}{2}~(u^0_{1,2}+u^0_{2,1}) \end{bmatrix} \end{align} }[/math]

and

[math]\displaystyle{ \begin{align} \begin{bmatrix}M_{11} \\ M_{22} \\ M_{12} \end{bmatrix} & = \int_{-h}^h x_3~\begin{bmatrix} C_{11} & C_{12} & 0 \\ C_{12} & C_{22} & 0 \\ 0 & 0 & C_{66} \end{bmatrix} \begin{bmatrix}\varepsilon_{11} \\ \varepsilon_{22} \\ \varepsilon_{12} \end{bmatrix} dx_3 \\[5pt] & = -\left\{ \int_{-h}^h x_3^2~\begin{bmatrix} C_{11} & C_{12} & 0 \\ C_{12} & C_{22} & 0 \\ 0 & 0 & C_{66} \end{bmatrix}~dx_3 \right\} \begin{bmatrix} \varphi_{1,1} \\ \varphi_{2,2} \\ \frac{1}{2}(\varphi_{1,2}+\varphi_{2,1}) \end{bmatrix} \end{align} }[/math]

For the shear terms

[math]\displaystyle{ \begin{bmatrix}Q_1 \\ Q_2 \end{bmatrix} = \kappa~\int_{-h}^h \begin{bmatrix} C_{55} & 0 \\ 0 & C_{44} \end{bmatrix} \begin{bmatrix}\varepsilon_{31} \\ \varepsilon_{32} \end{bmatrix} dx_3 = \cfrac{\kappa}{2}\left\{ \int_{-h}^h \begin{bmatrix} C_{55} & 0 \\ 0 & C_{44} \end{bmatrix}~dx_3 \right\} \begin{bmatrix} w^0_{,1} - \varphi_1 \\ w^0_{,2} - \varphi_2 \end{bmatrix} }[/math]

The extensional stiffnesses are the quantities

[math]\displaystyle{ A_{\alpha\beta} := \int_{-h}^h C_{\alpha\beta}~dx_3 }[/math]

The bending stiffnesses are the quantities

[math]\displaystyle{ D_{\alpha\beta} := \int_{-h}^h x_3^2~C_{\alpha\beta}~dx_3 \,. }[/math]

Mindlin theory for isotropic plates

For uniformly thick, homogeneous, and isotropic plates, the stress–strain relations in the plane of the plate are

[math]\displaystyle{ \begin{bmatrix}\sigma_{11} \\ \sigma_{22} \\ \sigma_{12} \end{bmatrix} = \cfrac{E}{1-\nu^2} \begin{bmatrix} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & \cfrac{1-\nu}{2} \end{bmatrix} \begin{bmatrix}\varepsilon_{11} \\ \varepsilon_{22} \\ 2\varepsilon_{12} \end{bmatrix} \,. }[/math]

where [math]\displaystyle{ E }[/math] is the Young's modulus, [math]\displaystyle{ \nu }[/math] is the Poisson's ratio, and [math]\displaystyle{ \varepsilon_{\alpha\beta} }[/math] are the in-plane strains. The through-the-thickness shear stresses and strains are related by

[math]\displaystyle{ \sigma_{31} = 2G\varepsilon_{31} \quad \text{and} \quad \sigma_{32} = 2G\varepsilon_{32} }[/math]

where [math]\displaystyle{ G = E/(2(1+\nu)) }[/math] is the shear modulus.

Constitutive relations

The relations between the stress resultants and the generalized deformations are,

[math]\displaystyle{ \begin{align} \begin{bmatrix}N_{11} \\ N_{22} \\ N_{12} \end{bmatrix} & = \cfrac{2Eh}{1-\nu^2} \begin{bmatrix} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & 1-\nu \end{bmatrix} \begin{bmatrix} u^0_{1,1} \\ u^0_{2,2} \\ \frac{1}{2}~(u^0_{1,2}+u^0_{2,1}) \end{bmatrix}, \\[5pt] \begin{bmatrix}M_{11} \\ M_{22} \\ M_{12} \end{bmatrix} & = -\cfrac{2Eh^3}{3(1-\nu^2)} \begin{bmatrix} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & 1-\nu \end{bmatrix} \begin{bmatrix} \varphi_{1,1} \\ \varphi_{2,2} \\ \frac{1}{2}(\varphi_{1,2}+\varphi_{2,1}) \end{bmatrix}, \end{align} }[/math]

and

[math]\displaystyle{ \begin{bmatrix}Q_1 \\ Q_2 \end{bmatrix} = \kappa G 2 h \begin{bmatrix} w^0_{,1} - \varphi_1 \\ w^0_{,2} - \varphi_2 \end{bmatrix} \,. }[/math]

The bending rigidity is defined as the quantity

[math]\displaystyle{ D = \cfrac{2Eh^3}{3(1-\nu^2)} \,. }[/math]

For a plate of thickness [math]\displaystyle{ h }[/math] ([math]\displaystyle{ h }[/math] of the following all indicates thickness), the bending rigidity has the form

[math]\displaystyle{ D = \cfrac{Eh^3}{12(1-\nu^2)} \,. }[/math]

Governing equations

If we ignore the in-plane extension of the plate, the governing equations are

[math]\displaystyle{ \begin{align} M_{\alpha\beta,\beta}-Q_\alpha & = 0 \\ Q_{\alpha,\alpha}+q & = 0 \,. \end{align} }[/math]

In terms of the generalized deformations, these equations can be written as

[math]\displaystyle{ \begin{align} &\nabla^2 \left(\frac{\partial \varphi_1}{\partial x_1} + \frac{\partial \varphi_2}{\partial x_2}\right) = \frac{q}{D} \\ &\nabla^2 w^0 - \frac{\partial \varphi_1}{\partial x_1} - \frac{\partial \varphi_2}{\partial x_2} = -\frac{q}{\kappa G h} \\ &\nabla^2 \left(\frac{\partial \varphi_1}{\partial x_2} - \frac{\partial \varphi_2}{\partial x_1}\right) = \frac{2\kappa G h}{D(1-\nu)}\left(\frac{\partial \varphi_1}{\partial x_2} - \frac{\partial \varphi_2}{\partial x_1}\right) \,. \end{align} }[/math]

Derivation of equilibrium equations in terms of deformations

If we expand out the governing equations of a Mindlin plate, we have [math]\displaystyle{ \begin{align} \frac{\partial M_{11}}{\partial x_1} + \frac{\partial M_{12}}{\partial x_2} & = Q_1 \quad\,,\quad \frac{\partial M_{21}}{\partial x_1} + \frac{\partial M_{22}}{\partial x_2} = Q_2 \\ \frac{\partial Q_1}{\partial x_1} + \frac{\partial Q_2}{\partial x_2} & = - q \,. \end{align} }[/math] Recalling that [math]\displaystyle{ M_{11} = -D\left(\frac{\partial \varphi_1}{\partial x_1}+\nu\frac{\partial \varphi_2}{\partial x_2}\right) ~,~~ M_{22} = -D\left(\frac{\partial \varphi_2}{\partial x_2}+\nu\frac{\partial \varphi_1}{\partial x_1}\right) ~,~~ M_{12} = -\frac{D(1-\nu)}{2}\left(\frac{\partial \varphi_1}{\partial x_2}+\frac{\partial \varphi_2}{\partial x_1}\right) }[/math] and combining the three governing equations, we have [math]\displaystyle{ \frac{\partial^3\varphi_1}{\partial x_1^3} + \frac{\partial^3 \varphi_1}{\partial x_1 \, \partial x_2^2} + \frac{\partial^3 \varphi_2}{\partial x_1^2 \, \partial x_2}+ \frac{\partial^3 \varphi_2}{\partial x_2^3}= \frac{q}{D} \,. }[/math] If we define [math]\displaystyle{ \mathcal{M} := D \left(\frac{\partial \varphi_1}{\partial x_1} + \frac{\partial \varphi_2}{\partial x_2}\right) }[/math] we can write the above equation as [math]\displaystyle{ \nabla^2 \mathcal{M} = q \,. }[/math] Similarly, using the relationships between the shear force resultants and the deformations, and the equation for the balance of shear force resultants, we can show that [math]\displaystyle{ \kappa G h \left(\nabla^2 w^0 - \frac{\mathcal{M}}{D}\right) = -q \,. }[/math] Since there are three unknowns in the problem, [math]\displaystyle{ \varphi_1 }[/math], [math]\displaystyle{ \varphi_2 }[/math], and [math]\displaystyle{ w^0 }[/math], we need a third equation which can be found by differentiating the expressions for the shear force resultants and the governing equations in terms of the moment resultants, and equating these. The resulting equation has the form [math]\displaystyle{ \nabla^2 \left(\frac{\partial \varphi_1}{\partial x_2} - \frac{\partial \varphi_2}{\partial x_1}\right) = \frac{2\kappa G h}{D(1-\nu)}\left(\frac{\partial \varphi_1}{\partial x_2} - \frac{\partial \varphi_2}{\partial x_1}\right) \,. }[/math] Therefore, the three governing equations in terms of the deformations are [math]\displaystyle{ \begin{align} &\nabla^2 \left(\frac{\partial \varphi_1}{\partial x_1} + \frac{\partial \varphi_2}{\partial x_2}\right) = \frac{q}{D} \\ &\nabla^2 w^0 - \frac{\partial \varphi_1}{\partial x_1} - \frac{\partial \varphi_2}{\partial x_2} = -\frac{q}{\kappa G h} \\ &\nabla^2 \left(\frac{\partial \varphi_1}{\partial x_2} - \frac{\partial \varphi_2}{\partial x_1}\right) = \frac{2\kappa G h}{D(1-\nu)}\left(\frac{\partial \varphi_1}{\partial x_2} - \frac{\partial \varphi_2}{\partial x_1}\right) \,. \end{align} }[/math]

The boundary conditions along the edges of a rectangular plate are

[math]\displaystyle{ \begin{align} \text{simply supported} \quad & \quad w^0 = 0, M_{11} = 0 ~(\text{or}~M_{22} = 0), \varphi_1 = 0 ~(\text{ or } \varphi_2 = 0) \\ \text{clamped} \quad & \quad w^0 = 0, \varphi_1 = 0, \varphi_{2} = 0 \,. \end{align} }[/math]

Relationship to Reissner's static theory

The canonical constitutive relations for shear deformation theories of isotropic plates can be expressed as

[math]\displaystyle{ \begin{align} M_{11} & = D\left[\mathcal{A}\left(\frac{\partial \varphi_1}{\partial x_1}+\nu\frac{\partial \varphi_2}{\partial x_2}\right) - (1-\mathcal{A})\left(\frac{\partial^2 w^0}{\partial x_1^2} + \nu\frac{\partial^2 w^0}{\partial x_2^2}\right)\right] + \frac{q}{1-\nu}\,\mathcal{B}\\[5pt] M_{22} & = D\left[\mathcal{A}\left(\frac{\partial \varphi_2}{\partial x_2}+\nu\frac{\partial \varphi_1}{\partial x_1}\right) - (1-\mathcal{A})\left(\frac{\partial^2 w^0}{\partial x_2^2} + \nu\frac{\partial^2 w^0}{\partial x_1^2}\right)\right] + \frac{q}{1-\nu}\,\mathcal{B}\\[5pt] M_{12} & = \frac{D(1-\nu)}{2}\left[\mathcal{A}\left(\frac{\partial \varphi_1}{\partial x_2}+\frac{\partial \varphi_2}{\partial x_1}\right) - 2(1-\mathcal{A})\,\frac{\partial^2 w^0}{\partial x_1 \partial x_2}\right] \\ Q_1 & = \mathcal{A} \kappa G h\left(\varphi_1 + \frac{\partial w^0}{\partial x_1}\right) \\[5pt] Q_2 & = \mathcal{A} \kappa G h\left(\varphi_2 + \frac{\partial w^0}{\partial x_2}\right) \,. \end{align} }[/math]

Note that the plate thickness is [math]\displaystyle{ h }[/math] (and not [math]\displaystyle{ 2h }[/math]) in the above equations and [math]\displaystyle{ D = Eh^3/[12(1-\nu^2)] }[/math]. If we define a Marcus moment,

[math]\displaystyle{ \mathcal{M} = D\left[\mathcal{A}\left(\frac{\partial \varphi_1}{\partial x_1} + \frac{\partial \varphi_2}{\partial x_2}\right) - (1-\mathcal{A})\nabla^2 w^0\right] + \frac{2q}{1-\nu^2}\mathcal{B} }[/math]

we can express the shear resultants as

[math]\displaystyle{ \begin{align} Q_1 & = \frac{\partial \mathcal{M}}{\partial x_1} + \frac{D(1-\nu)}{2}\left[\mathcal{A}\frac{\partial }{\partial x_2}\left(\frac{\partial \varphi_1}{\partial x_2} -\frac{\partial \varphi_2}{\partial x_1}\right)\right] - \frac{\mathcal{B}}{1+\nu}\frac{\partial q}{\partial x_1} \\[5pt] Q_2 & = \frac{\partial \mathcal{M}}{\partial x_2} - \frac{D(1-\nu)}{2}\left[\mathcal{A}\frac{\partial }{\partial x_1}\left(\frac{\partial \varphi_1}{\partial x_2} -\frac{\partial \varphi_2}{\partial x_1}\right)\right] - \frac{\mathcal{B}}{1+\nu}\frac{\partial q}{\partial x_2}\,. \end{align} }[/math]

These relations and the governing equations of equilibrium, when combined, lead to the following canonical equilibrium equations in terms of the generalized displacements.

[math]\displaystyle{ \begin{align} & \nabla^2 \left(\mathcal{M} - \frac{\mathcal{B}}{1+\nu}\,q\right) = -q \\ & \kappa G h\left(\nabla^2 w^0 + \frac{\mathcal{M}}{D}\right) = -\left(1 - \cfrac{\mathcal{B} c^2}{1+\nu}\right)q \\ & \nabla^2 \left(\frac{\partial \varphi_1}{\partial x_2} - \frac{\partial \varphi_2}{\partial x_1}\right) = c^2\left(\frac{\partial \varphi_1}{\partial x_2} - \frac{\partial \varphi_2}{\partial x_1}\right) \end{align} }[/math]

where

[math]\displaystyle{ c^2 = \frac{2\kappa G h}{D(1-\nu)} \,. }[/math]

In Mindlin's theory, [math]\displaystyle{ w^0 }[/math] is the transverse displacement of the mid-surface of the plate and the quantities [math]\displaystyle{ \varphi_1 }[/math] and [math]\displaystyle{ \varphi_2 }[/math] are the rotations of the mid-surface normal about the [math]\displaystyle{ x_2 }[/math] and [math]\displaystyle{ x_1 }[/math]-axes, respectively. The canonical parameters for this theory are [math]\displaystyle{ \mathcal{A} = 1 }[/math] and [math]\displaystyle{ \mathcal{B} = 0 }[/math]. The shear correction factor [math]\displaystyle{ \kappa }[/math] usually has the value [math]\displaystyle{ 5/6 }[/math].

On the other hand, in Reissner's theory, [math]\displaystyle{ w^0 }[/math] is the weighted average transverse deflection while [math]\displaystyle{ \varphi_1 }[/math] and [math]\displaystyle{ \varphi_2 }[/math] are equivalent rotations which are not identical to those in Mindlin's theory.

Relationship to Kirchhoff–Love theory

If we define the moment sum for Kirchhoff–Love theory as

[math]\displaystyle{ \mathcal{M}^K := -D\nabla^2 w^K }[/math]

we can show that

[math]\displaystyle{ \mathcal{M} = \mathcal{M}^K + \frac{\mathcal{B}}{1+\nu}\,q + D \nabla^2 \Phi }[/math]

where [math]\displaystyle{ \Phi }[/math] is a biharmonic function such that [math]\displaystyle{ \nabla^2 \nabla^2 \Phi = 0 }[/math]. We can also show that, if [math]\displaystyle{ w^K }[/math] is the displacement predicted for a Kirchhoff–Love plate,

[math]\displaystyle{ w^0 = w^K + \frac{\mathcal{M}^K}{\kappa G h}\left(1 - \frac{\mathcal{B} c^2}{2}\right) - \Phi + \Psi }[/math]

where [math]\displaystyle{ \Psi }[/math] is a function that satisfies the Laplace equation, [math]\displaystyle{ \nabla^2 \Psi = 0 }[/math]. The rotations of the normal are related to the displacements of a Kirchhoff–Love plate by

[math]\displaystyle{ \begin{align} \varphi_1 = - \frac{\partial w^K}{\partial x_1} - \frac{1}{\kappa G h}\left(1 - \frac{1}{\mathcal{A}} - \frac{\mathcal{B} c^2}{2}\right)Q_1^K + \frac{\partial }{\partial x_1}\left(\frac{D}{\kappa G h \mathcal{A}}\nabla^2 \Phi + \Phi - \Psi\right) + \frac{1}{c^2}\frac{\partial \Omega}{\partial x_2} \\ \varphi_2 = - \frac{\partial w^K}{\partial x_2} - \frac{1}{\kappa G h}\left(1 - \frac{1}{\mathcal{A}} - \frac{\mathcal{B} c^2}{2}\right)Q_2^K + \frac{\partial }{\partial x_2}\left(\frac{D}{\kappa G h \mathcal{A}}\nabla^2 \Phi + \Phi - \Psi\right) + \frac{1}{c^2}\frac{\partial \Omega}{\partial x_1} \end{align} }[/math]

where

[math]\displaystyle{ Q_1^K = -D\frac{\partial }{\partial x_1}\left(\nabla^2 w^K\right) ~,~~ Q_2^K = -D\frac{\partial }{\partial x_2}\left(\nabla^2 w^K\right) ~,~~ \Omega := \frac{\partial \varphi_1}{\partial x_2} - \frac{\partial \varphi_2}{\partial x_1} \,. }[/math]

See also

• Bending
• Bending of plates
• Infinitesimal strain theory
• Linear elasticity
• Plate theory
• Stress (mechanics)
• Stress resultants
• Vibration of plates