Physics:Neoclassical transport

Short description: Type of plasma diffusion

In plasma physics and magnetic confinement fusion, neoclassical transport or neoclassical diffusion is a theoretical description of collisional transport in toroidal plasmas, usually found in tokamaks or stellerators. It is a modification of classical diffusion adding in effects of non-uniform magnetic fields due to the toroidal geometry, which give rise to new diffusion effects.

Description

Classical diffusion occurs when ions orbiting separate paths around the reactor collide, causing the ions to fuse or scatter to new locations. Scattering causes the plasma as a whole to diffuse outward from its magnetic container.

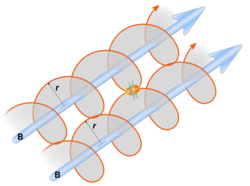
Classical transport models a plasma in a magnetic field as a large number of particles traveling in helical paths around a line of force. In typical reactor designs, the lines are roughly parallel, so particles orbiting adjacent lines may collide and scatter. This results in a random walk process which eventually leads to the particles finding themselves outside the magnetic field.

Neoclassical transport adds the effects of the geometry of the fields. In particular, it considers the field inside the tokamak and similar toroidal arrangements, where the field is stronger on the inside curve than the outside simply due to the magnets being closer together in that area. To even out these forces, the field as a whole is twisted into a helix, so that the particles alternately move from the inside to the outside of the reactor.

In this case, as the particle transits from the outside to the inside, it sees an increasing magnetic force. If the particle energy is low, this increasing field may cause the particle to reverse directions, as in a magnetic mirror. The particle now travels in the reverse direction through the reactor, to the outside limit, and then back towards the inside where the same reflection process occurs. This leads to a population of particles bouncing back and forth between two points, tracing out a path that looks like a banana from above, the so-called banana orbits.

Since any particle in the long tail of the Maxwell–Boltzmann distribution is subject to this effect, there is always some natural population of such banana particles. Since these travel in the reverse direction for half of their orbit, their drift behavior is oscillatory in space. Therefore, when the particles collide, their average step size (width of the banana) is much larger than their gyroradius, leading to neoclassical diffusion across the magnetic field.

Trapped particles and banana orbits

A consequence of the toroidal geometry to the guiding-center orbits is that some particles can be reflected on the trajectory from the outboard side to the inboard side due to the presence of magnetic field gradients, similar to a magnetic mirror. The reflected particles cannot do a full turn in the poloidal plane and are trapped which follow the banana orbits.

This can be demonstrated by considering tokamak equilibria for low-[math]\displaystyle{ \beta }[/math] and large aspect ratio which have nearly circular cross sections, where polar coordinates [math]\displaystyle{ (r,\theta) }[/math] centered at the magnetic axis can be used with [math]\displaystyle{ r=\text{constant} }[/math] approximately describing the flux surfaces. The magnitude of the total magnetic field can be approximated by the following expression:

[math]\displaystyle{ B \approx B_{0}(1- \epsilon \cos{\theta}) }[/math]

where the subscript [math]\displaystyle{ 0 }[/math] indicates value at the magnetic axis [math]\displaystyle{ (r=0) }[/math], [math]\displaystyle{ R }[/math] is the major radius, [math]\displaystyle{ \epsilon=r/R_{0} }[/math] is the inverse aspect ratio, and [math]\displaystyle{ B }[/math] is the magnetic field. The parallel component of the drift-ordered guiding-center orbits in this magnetic field, assuming no electric field, is given by:

[math]\displaystyle{ m\dot{v}_{\parallel}= -\mu \nabla_{\parallel}B = - \nabla_{\parallel}(U(\theta)) }[/math]

where [math]\displaystyle{ m }[/math] is the particle mass, [math]\displaystyle{ \boldsymbol{v} }[/math] is the velocity, and [math]\displaystyle{ \mu=mv_{\perp}^{2}/2B }[/math] is the magnetic moment (first adiabatic invariant). The direction in the subscript indicates parallel or perpendicular to the magnetic filed. [math]\displaystyle{ U(\theta)=\mu B_{0}(1-\epsilon \cos{\theta}) }[/math] is the effective potential reflecting the conservation of kinetic energy [math]\displaystyle{ \mathcal{E} = mv_{\parallel}^{2}/2 + mv_{\perp}^{2}/2 = mv_{\parallel}^{2}/2 + U = \text{constant} }[/math].

The parallel trajectory experiences a mirror force where the particle moving into a magnetic field of increasing magnitude can be reflected by this force. If a magnetic field has a minimum along a field line, the particles in this region of weaker field can be trapped. This is indeed true given the form of [math]\displaystyle{ B }[/math] we use. The particles are reflected (trapped particles) for sufficiently large [math]\displaystyle{ v_{\perp} \gt v_{\parallel} }[/math] or complete their poloidal turn (passing particles) otherwise.

To see this in detail, the maximum and minimum of the effective potential can be identified as [math]\displaystyle{ U_{\min}=\mu B_{0} (1 - \epsilon) }[/math] and [math]\displaystyle{ U_{\max}=\mu B_{0} (1 + \epsilon) }[/math]. The passing particles have [math]\displaystyle{ \mathcal{E} \gt U_{\max} }[/math] and the trapped particles have [math]\displaystyle{ U_{\min} \lt \mathcal{E} \leq U_{\max} }[/math]. Recognising this and define a constant of motion [math]\displaystyle{ \lambda = \mu B_{0}/\mathcal{E} \geq 0 }[/math], we have

• Passing: [math]\displaystyle{ 0 \leq \lambda \lt 1 - \epsilon }[/math]
• Trapped: [math]\displaystyle{ 1 - \epsilon \lt \lambda \leq 1+\epsilon }[/math]

Orbit width

The orbit width [math]\displaystyle{ \Delta r }[/math] can be estimated by considering the variation in [math]\displaystyle{ v_{\parallel} }[/math] over an orbit period [math]\displaystyle{ \Delta r \sim \Delta v_{\parallel}/\Omega_{\text{p}} }[/math]. Using the conservation of [math]\displaystyle{ \mathcal{E} }[/math] and [math]\displaystyle{ \mu }[/math],

[math]\displaystyle{ v_{\parallel} = \pm v\sqrt{1- \lambda B / B_{0}} \approx \pm v \sqrt{1-\lambda(1-\epsilon \cos{\theta})} }[/math]

The orbit widths can then be estimated, which gives

• Passing width: [math]\displaystyle{ \Delta r_{\text{p}} \sim q \rho }[/math]
• Banana width: [math]\displaystyle{ \Delta r_{\text{b}} \sim q \rho / \sqrt{\epsilon} }[/math]

The bounce angle [math]\displaystyle{ \theta_{\text{b}} }[/math] at which [math]\displaystyle{ v_{\parallel} }[/math] becomes zero for the trapped particles is

[math]\displaystyle{ v_{\parallel}(\theta_{\text{b}})=0 \quad \Rightarrow \quad \cos{\theta_{\text{b}}}= \frac{\lambda -1}{\epsilon \lambda} }[/math]

Bounce time

The bounce time [math]\displaystyle{ \tau_{\text{b}} }[/math] is the time required for a particle to complete its poloidal orbit. This is calculated by

[math]\displaystyle{ \tau_{\text{b}}=\int \text{d}t = \oint \frac{\text{d}\theta}{\dot{\theta}}=\oint \frac{\text{d}\theta}{v_{\parallel} \boldsymbol{b} \cdot \nabla \theta} \simeq \frac{B}{B_{\theta}} \oint \frac{r\text{d}\theta}{\sigma v \sqrt{1-\lambda(1-\epsilon \cos{\theta}})} }[/math]

where [math]\displaystyle{ \sigma = \pm1 }[/math]. The integral can be rewritten as

[math]\displaystyle{ \tau_{\text{b}} \simeq \frac{qR}{v\sqrt{2\epsilon \lambda}} \oint \frac{\text{d}\theta}{\sigma \sqrt{k^{2} - \sin^{2}(\theta/2)}} }[/math]

where [math]\displaystyle{ q=rB_{\phi}/RB_{\theta} }[/math] and [math]\displaystyle{ k^{2} \equiv [1-\lambda(1-\epsilon)] / 2\epsilon \lambda }[/math], which is also equivalent to [math]\displaystyle{ \sin^{2}(\theta_{\text{b}}/2) }[/math] for trapped particles. This can be evaluated using the results from the complete elliptic integral of the first kind

[math]\displaystyle{ K(k) \equiv \int_{0}^{\pi/2} \frac{\text{d}x}{\sqrt{1-k^{2}\sin^{2}x}}, \quad 0\lt k \leq 1 }[/math]

with properties

[math]\displaystyle{ \begin{align} K(k) & = \frac{\pi}{2} (1+ \mathcal{O}(k^{2})) \quad &\text{for} \quad k \rightarrow 0\\ K(k) & \rightarrow \ln{\frac{4}{\sqrt{1-k^{2}}}} \quad &\text{for} \quad k \rightarrow 1 \end{align} }[/math]

The bounce time for passing particles is obtained by integrating between [math]\displaystyle{ [0,2 \pi] }[/math]

[math]\displaystyle{ \tau_{b}=\frac{4qR}{\sigma \sqrt{2\epsilon \lambda}} \frac{K(k^{-1})}{k} }[/math]

where the bounce time for trapped particle is evaluated by integrating between [math]\displaystyle{ [0,\theta_{\text{b}}] }[/math] and taking [math]\displaystyle{ \lambda \approx 1 }[/math]

[math]\displaystyle{ \tau_{b}=\frac{8qR}{\sigma \sqrt{2\epsilon}} K(k) }[/math]

The limiting cases are

• Super passing: [math]\displaystyle{ k \rightarrow \infty \quad \Rightarrow \quad K(k^{-1}) \rightarrow \pi /2 \quad \Rightarrow \quad \tau_{\text{b}} \rightarrow 2 \pi q R / v_{\parallel} }[/math]
• Super trapped: [math]\displaystyle{ k \rightarrow 0 \quad \Rightarrow \quad K(k) \rightarrow \pi /2 \quad \Rightarrow \quad \tau_{\text{b}} \rightarrow (2 \pi q R / v_{\parallel} )\sqrt{2/\epsilon} }[/math]
• Barely trapped: [math]\displaystyle{ k \rightarrow 1 \quad \Rightarrow \quad K(k) \rightarrow \infty \quad \Rightarrow \quad \tau_{\text{b}} \rightarrow \infty }[/math]

See also

• Wendelstein 7-X

References

• Wagner, F.; Wobig, H. (2005). "Magnetic Confinement". in Dinklage, Andreas; Klinger, Thomas; Marx, Gerrit et al.. Plasma Physics: Confinement, Transport and Collective Effects. Springer.