Field line
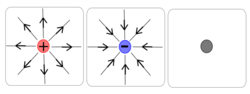
A field line is a graphical visual aid for visualizing vector fields. It consists of an imaginary integral curve which is tangent to the field vector at each point along its length.[1][2] A diagram showing a representative set of neighboring field lines is a common way of depicting a vector field in scientific and mathematical literature; this is called a field line diagram. They are used to show electric fields, magnetic fields, and gravitational fields among many other types. In fluid mechanics field lines showing the velocity field of a fluid flow are called streamlines.
Definition and description

A vector field defines a direction and magnitude at each point in space. A field line is an integral curve for that vector field and may be constructed by starting at a point and tracing a line through space that follows the direction of the vector field, by making the field line tangent to the field vector at each point.[3][2][1] A field line is usually shown as a directed line segment, with an arrowhead indicating the direction of the vector field. For two-dimensional fields the field lines are plane curves; since a plane drawing of a 3-dimensional set of field lines can be visually confusing most field line diagrams are of this type. Since at each point where it is nonzero and finite the vector field has a unique direction, field lines can never intersect, so there is exactly one field line passing through each point at which the vector field is nonzero and finite.[3][2] Points where the field is zero or infinite have no field line through them, since direction cannot be defined there, but can be the endpoints of field lines.
Since there are an infinite number of points in any region, an infinite number of field lines can be drawn; but only a limited number can be shown on a field line diagram. Therefore which field lines are shown is a choice made by the person or computer program which draws the diagram, and a single vector field may be depicted by different sets of field lines. A field line diagram is necessarily an incomplete description of a vector field, since it gives no information about the field between the drawn field lines, and the choice of how many and which lines to show determines how much useful information the diagram gives.
An individual field line shows the direction of the vector field but not the magnitude. In order to also depict the magnitude of the field, field line diagrams are often drawn so that each line represents the same quantity of flux. Then the density of field lines (number of field lines per unit perpendicular area) at any location is proportional to the magnitude of the vector field at that point. Areas in which neighboring field lines are converging (getting closer together) indicates that the field is getting stronger in that direction.
In vector fields which have nonzero divergence, field lines begin on points of positive divergence (sources) and end on points of negative divergence (sinks), or extend to infinity. For example, electric field lines begin on positive electric charges and end on negative charges. In fields which are divergenceless (solenoidal), such as magnetic fields, field lines have no endpoints; they are either closed loops or are endless.[4][5]
In physics, drawings of field lines are mainly useful in cases where the sources and sinks, if any, have a physical meaning, as opposed to e.g. the case of a force field of a radial harmonic. For example, Gauss's law states that an electric field has sources at positive charges, sinks at negative charges, and neither elsewhere, so electric field lines start at positive charges and end at negative charges. A gravitational field has no sources, it has sinks at masses, and it has neither elsewhere, gravitational field lines come from infinity and end at masses. A magnetic field has no sources or sinks (Gauss's law for magnetism), so its field lines have no start or end: they can only form closed loops, extend to infinity in both directions, or continue indefinitely without ever crossing itself. However, as stated above, a special situation may occur around points where the field is zero (that cannot be intersected by field lines, because their direction would not be defined) and the simultaneous begin and end of field lines takes place. This situation happens, for instance, in the middle between two identical positive electric point charges. There, the field vanishes and the lines coming axially from the charges end. At the same time, in the transverse plane passing through the middle point, an infinite number of field lines diverge radially. The concomitant presence of the lines that end and begin preserves the divergence-free character of the field in the point.[5]
Note that for this kind of drawing, where the field-line density is intended to be proportional to the field magnitude, it is important to represent all three dimensions. For example, consider the electric field arising from a single, isolated point charge. The electric field lines in this case are straight lines that emanate from the charge uniformly in all directions in three-dimensional space. This means that their density is proportional to , the correct result consistent with Coulomb's law for this case. However, if the electric field lines for this setup were just drawn on a two-dimensional plane, their two-dimensional density would be proportional to , an incorrect result for this situation.[6]
Construction

Given a vector field and a starting point a field line can be constructed iteratively by finding the field vector at that point . The unit tangent vector at that point is: . By moving a short distance along the field direction a new point on the line can be found Then the field at that point is found and moving a further distance in that direction the next point of the field line is found. At each point the next point can be found by By repeating this and connecting the points, the field line can be extended as far as desired. This is only an approximation to the actual field line, since each straight segment isn't actually tangent to the field along its length, just at its starting point. But by using a small enough value for , taking a greater number of shorter steps, the field line can be approximated as closely as desired. The field line can be extended in the opposite direction from by taking each step in the opposite direction by using a negative step .
Examples

If the vector field describes a velocity field, then the field lines follow stream lines in the flow. Perhaps the most familiar example of a vector field described by field lines is the magnetic field, which is often depicted using field lines emanating from a magnet.
Divergence and curl
Field lines can be used to trace familiar quantities from vector calculus:
- Divergence may be easily seen through field lines, assuming the lines are drawn such that the density of field lines is proportional to the magnitude of the field (see above). In this case, the divergence may be seen as the beginning and ending of field lines. If the vector field is the resultant of radial inverse-square law fields with respect to one or more sources then this corresponds to the fact that the divergence of such a field is zero outside the sources. In a solenoidal vector field (i.e., a vector field where the divergence is zero everywhere), the field lines neither begin nor end; they either form closed loops, or go off to infinity in both directions. If a vector field has positive divergence in some area, there will be field lines starting from points in that area. If a vector field has negative divergence in some area, there will be field lines ending at points in that area.
- The Kelvin–Stokes theorem shows that field lines of a vector field with zero curl (i.e., a conservative vector field, e.g. a gravitational field or an electrostatic field) cannot be closed loops. In other words, curl is always present when a field line forms a closed loop. It may be present in other situations too, such as a helical shape of field lines.
Physical significance
File:16. Магнетни силови линии.ogv
While field lines are a "mere" mathematical construction, in some circumstances they take on physical significance. In fluid mechanics, the velocity field lines (streamlines) in steady flow represent the paths of particles of the fluid. In the context of plasma physics, electrons or ions that happen to be on the same field line interact strongly, while particles on different field lines in general do not interact. This is the same behavior that the particles of iron filings exhibit in a magnetic field.
The iron filings in the photo appear to be aligning themselves with discrete field lines, but the situation is more complex. It is easy to visualize as a two-stage-process: first, the filings are spread evenly over the magnetic field but all aligned in the direction of the field. Then, based on the scale and ferromagnetic properties of the filings they damp the field to either side, creating the apparent spaces between the lines that we see.[citation needed] Of course the two stages described here happen concurrently until an equilibrium is achieved. Because the intrinsic magnetism of the filings modifies the field, the lines shown by the filings are only an approximation of the field lines of the original magnetic field. Magnetic fields are continuous, and do not have discrete lines.
See also
- Force field
- Field lines of Julia sets
- External ray — field lines of Douady–Hubbard potential of Mandelbrot set or filled-in Julia sets
- Line of force
- Vector field
- Line integral convolution
References
- ↑ 1.0 1.1 Tou, Stephen (2011). Visualization of Fields and Applications in Engineering. John Wiley and Sons. pp. 64. ISBN 9780470978467. https://books.google.com/books?id=4kjP1ALPTfUC&q=%22field+line%22+vector+field+tangent&pg=PT64.
- ↑ 2.0 2.1 2.2 Durrant, Alan (1996). Vectors in Physics and Engineering. CRC Press. pp. 129–130. ISBN 9780412627101. https://books.google.com/books?id=NCljosTG6bYC&q=%22field+line%22+vector+field+tangent&pg=PA129.
- ↑ 3.0 3.1 Haus, Herman A.; Mechior, James R. (1998). "Section 2.7: Visualization of Fields and the Divergence and Curl". Electromagnetic fields and energy. Hypermedia Teaching Facility, Massachusetts Institute of Technology. http://web.mit.edu/6.013_book/www/chapter2/2.7.html.
- ↑ Lieberherr, Martin (6 July 2010). "The magnetic field lines of a helical coil are not simple loops". American Journal of Physics 78 (11): 1117–1119. doi:10.1119/1.3471233. Bibcode: 2010AmJPh..78.1117L.
- ↑ 5.0 5.1 Zilberti, Luca (25 April 2017). "The Misconception of Closed Magnetic Flux Lines". IEEE Magnetics Letters 8: 1–5. doi:10.1109/LMAG.2017.2698038. https://ieeexplore.ieee.org/document/7911292.
- ↑ A. Wolf, S. J. Van Hook, E. R. Weeks, Electric field line diagrams don't work Am. J. Phys., Vol. 64, No. 6. (1996), pp. 714–724 DOI 10.1119/1.18237
Further reading
- Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. pp. 65–67 and 232. ISBN 978-0-13-805326-0. https://archive.org/details/introductiontoel00grif_0/page/65.
External links
- Interactive Java applet showing the electric field lines of selected pairs of charges by Wolfgang Bauer
- "Visualization of Fields and the Divergence and Curl" course notes from a course at the Massachusetts Institute of Technology.
 |
