Physics:Orbital angular momentum of light
The orbital angular momentum of light (OAM) is the component of angular momentum of a light beam that is dependent on the field spatial distribution, and not on the polarization. It can be further split into an internal and an external OAM. The internal OAM is an origin-independent angular momentum of a light beam that can be associated with a helical or twisted wavefront. The external OAM is the origin-dependent angular momentum that can be obtained as cross product of the light beam position (center of the beam) and its total linear momentum. File:Focused Laguerre-Gaussian beam.webm
Concept
A beam of light carries a linear momentum [math]\displaystyle{ \mathbf{P} }[/math], and hence it can be also attributed an external angular momentum [math]\displaystyle{ \mathbf{L}_e=\mathbf{r}\times\mathbf{P} }[/math]. This external angular momentum depends on the choice of the origin of the coordinate system. If one chooses the origin at the beam axis and the beam is cylindrically symmetric (at least in its momentum distribution), the external angular momentum will vanish. The external angular momentum is a form of OAM, because it is unrelated to polarization and depends on the spatial distribution of the optical field (E).
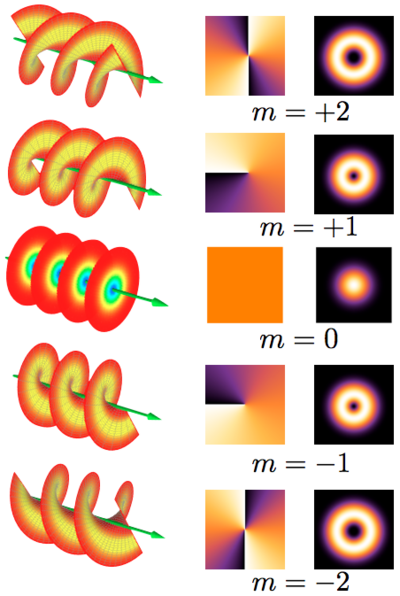
A more interesting example of OAM is the internal OAM appearing when a paraxial light beam is in a so-called "helical mode". Helical modes of the electromagnetic field are characterized by a wavefront that is shaped as a helix, with an optical vortex in the center, at the beam axis (see figure). If the phase varies around the axis of such a wave, it carries orbital angular momentum.[1]
In the figure to the right, the first column shows the beam wavefront shape. The second column is the optical phase distribution in a beam cross-section, shown in false colors. The third column is the light intensity distribution in a beam cross-section (with a dark vortex core at the center).
The helical modes are characterized by an integer number [math]\displaystyle{ m }[/math], positive or negative. If [math]\displaystyle{ m=0 }[/math], the mode is not helical and the wavefronts are multiple disconnected surfaces, for example, a sequence of parallel planes (from which the name "plane wave"). If [math]\displaystyle{ m=\pm 1 }[/math], the handedness determined by the sign of [math]\displaystyle{ m }[/math], the wavefront is shaped as a single helical surface, with a step length equal to the wavelength [math]\displaystyle{ \lambda }[/math]. If [math]\displaystyle{ |m|\geqslant 2 }[/math], the wavefront is composed of [math]\displaystyle{ |m| }[/math] distinct but intertwined helices, with the step length of each helix surface equal to [math]\displaystyle{ |m|\lambda }[/math], and a handedness given by the sign of [math]\displaystyle{ m }[/math]. The integer [math]\displaystyle{ m }[/math] is also the so-called "topological charge" of the optical vortex. Light beams that are in a helical mode carry nonzero OAM. As an example, any Laguerre-Gaussian mode with rotational mode number [math]\displaystyle{ l \ne 0 }[/math] has such a helical wavefront.[2]
Mathematical expressions for the orbital angular momentum of light
The classical expression of the orbital angular momentum in the paraxial limit[dubious ] is the following:[3] [math]\displaystyle{ \mathbf{L} = \epsilon_0 \sum_{i=x,y,z} \int \left(E^i\left(\mathbf{r} \times \boldsymbol{\nabla}\right) A^i\right)d^3\mathbf{r} , }[/math] where [math]\displaystyle{ \mathbf{E} }[/math] and [math]\displaystyle{ \mathbf{A} }[/math] are the electric field and the vector potential, respectively, [math]\displaystyle{ \epsilon_0 }[/math] is the vacuum permittivity and we are using SI units. The [math]\displaystyle{ i }[/math]-superscripted symbols denote the cartesian components of the corresponding vectors.
For a monochromatic wave this expression can be transformed into the following one:[4] [math]\displaystyle{ \mathbf{L}=\frac{\epsilon_0}{2i\omega}\sum_{i=x,y,z} \int \left({E^i}^{\ast}\left(\mathbf{r}\times\mathbf{\nabla}\right) E^i\right) d^3\mathbf{r} . }[/math]
This expression is generally nonvanishing when the wave is not cylindrically symmetric. In particular, in a quantum theory, individual photons may have the following values of the OAM: [math]\displaystyle{ \mathbf{L}_z = m\hbar . }[/math]
The corresponding wave functions (eigenfunctions of OAM operator) have the following general expression: [math]\displaystyle{ \langle \mathbf{r}|m\rangle\propto e^{i m \phi} . }[/math] where [math]\displaystyle{ \phi }[/math] is the cylindrical coordinate. As mentioned in the Introduction, this expression corresponds to waves having a helical wavefront (see figure above), with an optical vortex in the center, at the beam axis.
Production of OAM states

Orbital angular momentum states with [math]\displaystyle{ l = \pm 1 }[/math] occur naturally.[citation needed] OAM states of arbitrary [math]\displaystyle{ l }[/math] can be created artificially using a variety of tools, such as using spiral phase plates, spatial light modulators and q-plates.
Spiral wave plates, made of plastic or glass, are plates where the thickness of the material increases in a spiral pattern in order to imprint a phase gradient on light passing through it. For a given wavelength, an OAM state of a given [math]\displaystyle{ l }[/math] requires that the step height —the height between the thinnest and thickest parts of the plate— be given by [math]\displaystyle{ s = l\lambda/(n-1) }[/math] where [math]\displaystyle{ n }[/math] is an integer. Although the wave plates themselves are efficient, they are relatively expensive to produce, and are, in general, not adjustable to different wavelengths of light.[5]
Another way to modify the phase of the light is with a diffraction grating. For an [math]\displaystyle{ l=0 }[/math] state, the diffraction grating would consist of parallel lines. However, for an [math]\displaystyle{ l=1 }[/math] state, there will be a "fork" dislocation, and the number of lines above the dislocation will be one larger than below. An OAM state with [math]\displaystyle{ l\gt 1 }[/math] can be created by increasing the difference in the number of lines above and below the dislocation.[6] As with the spiral wave plates, these diffraction gratings are fixed for [math]\displaystyle{ l }[/math], but are not restricted to a particular wavelength.
A spatial light modulator operates in a similar way to diffraction gratings, but can be controlled by computer to dynamically generate a wide range of OAM states.
Recent advances
Theoretical work suggests that a series of optically distinct chromophores are capable of supporting an excitonic state whose symmetry is such that in the course of the exciton relaxing, a radiation mode of non-zero topological charge is created directly.[7]
Most recently,[when?] the geometric phase concept has been adopted for OAM generation. The geometric phase is modulated to coincide with the spatial phase dependence factor, i.e., [math]\displaystyle{ e^{i m \phi} }[/math] of an OAM carrying wave. In this way, geometric phase is introduced by using anisotropic scatterers. For example, a metamaterial composed of distributed linear polarizers in a rotational symmetric manner generates an OAM of order 1.[8] To generate higher-order OAM wave, nano-antennas which can produce the spin-orbit coupling effect are designed and then arranged to form a metasurface with different topological charges.[9] Consequently, the transmitted wave carries an OAM, and its order is twice the value of the topological charge. Usually, the conversion efficiency is not high for the transmission-type metasurface. Alternative solution to achieve high transmittance is to use complementary (Babinet-inverted) metasurface.[10] On the other hand, it is much easier to achieve high conversion efficiency, even 100% efficiency in the reflection-type metasurface such as the composite PEC-PMC metasurface.[11]
Beside OAM generation in free space, integrated photonic approaches can also realize on-chip optical vortices carrying OAM. Representative approaches include patterned ring resonators,[12] subwavelength holographic gratings,[13] Non-Hermitian vortex lasers,[14][15] and meta-waveguide OAM emitters.[16][17]
Potential use in telecommunications
Research into OAM has suggested that light waves could carry hitherto unprecedented quantities of data through optical fibres. According to preliminary tests, data streams travelling along a beam of light split into 8 different circular polarities have demonstrated the capacity to transfer up to 2.5 terabits of data (equivalent to 66 DVDs or 320 gigabytes) per second.[18] Further research into OAM multiplexing in the radio and mm wavelength frequencies has been shown in preliminary tests to be able to transmit 32 gigabits of data per second over the air. The fundamental communication limit of orbital-angular-momentum multiplexing is increasingly urgent for current multiple-input multiple-output (MIMO) research. The limit has been clarified in terms of independent scattering channels or the degrees of freedom (DoF) of scattered fields through angular-spectral analysis, in conjunction with a rigorous Green function method.[19] The DoF limit is universal for arbitrary spatial-mode multiplexing, which is launched by a planar electromagnetic device, such as antenna, metasurface, etc., with a predefined physical aperture.
Measuring the orbital angular momentum of light
Determining the spin angular momentum (SAM) of light is simple – SAM is related to the polarization state of the light: the AM is, per photon, in a left and right circularly polarized beam respectively. Thus the SAM can be measured by transforming the circular polarization of light into a p- or s-polarized state by means of a wave plate and then using a polarizing beam splitter that will transmit or reflect the state of light.[5]
The development of a simple and reliable method for the measurement of orbital angular momentum (OAM) of light, however, remains an important problem in the field of light manipulation. OAM (per photon) arises from the amplitude cross-section of the beam and is therefore independent of the spin angular momentum: whereas SAM has only two orthogonal states, the OAM is described by a state that can take any integer value N.[20] As the state of OAM of light is unbounded, any integer value of l is orthogonal to (independent from) all the others. Where a beam splitter could separate the two states of SAM, no device can separate the N (if greater than 2) modes of OAM, and, clearly, the perfect detection of all N potential states is required to finally resolve the issue of measuring OAM. Nevertheless, some methods have been investigated for the measurement of OAM.
Counting spiral fringes
Beams carrying OAM have a helical phase structure. Interfering such a beam with a uniform plane wave reveals phase information about the input beam through analysis of the observed spiral fringes. In a Mach–Zender interferometer, a helically phased source beam is made to interfere with a plane-wave reference beam along a collinear path. Interference fringes will be observed in the plane of the beam waist and/or at the Rayleigh range. The path being collinear, these fringes are pure consequence of the relative phase structure of the source beam. Each fringe in the pattern corresponds to one step through: counting the fringes suffices to determine the value of l.
Diffractive holographic filters
Computer-generated holograms can be used to generate beams containing phase singularities, and these have now become a standard tool for the generation of beams carrying OAM. This generating method can be reversed: the hologram, coupled to a single-mode fiber of set entrance aperture, becomes a filter for OAM. This approach is widely used for the detection of OAM at the single-photon level.
The phase of these optical elements results to be the superposition of several fork-holograms carrying topological charges selected in the set of values to be demultiplexed. The position of the channels in far-field can be controlled by multiplying each fork-hologram contribution to the corresponding spatial frequency carrier.[21]
Other methods
Other methods to measure the OAM of light include the rotational Doppler effect, systems based on a Dove prism interferometer,[22] the measure of the spin of trapped particles, the study of diffraction effects from apertures, and optical transformations.[23][24] The latter use diffractive optical elements in order to unwrap the angular phase patterns of OAM modes into plane-wave phase patterns which can subsequently be resolved in the Fourier space. The resolution of such schemes can be improved by spiral transformations that extend the phase range of the output strip-shaped modes by the number of spirals in the input beamwidth.[25]
Quantum-information applications
OAM states can be generated in coherent superpositions and they can be entangled,[26][27] which is an integral element of schemes for quantum information protocols. Photon pairs generated by the process of parametric down-conversion are naturally entangled in OAM,[28][29] and correlations measured using spatial light modulators (SLM).[30]
Using qudits (with d levels, as opposed to a qubit's 2 levels) has been shown to improve the robustness of quantum key distribution schemes. OAM states provide a suitable physical realisation of such a system, and a proof-of-principle experiment (with 7 OAM modes from [math]\displaystyle{ l = -3 }[/math] to [math]\displaystyle{ l = 3 }[/math]) has been demonstrated.[31]
Radio astronomy
In 2019, a letter published in the Monthly Notices of the Royal Astronomical Society presented evidence that OAM radio signals had been received from the vicinity of the M87* black hole, over 50 million light years distant, suggesting that optical angular momentum information can propagate over astronomical distances.[32]
See also
- Angular momentum
- Angular momentum of light
- Orbital angular momentum of free electrons
- Circular polarization
- Hypergeometric-Gaussian modes
- Laguerre-Gaussian modes
- Spin angular momentum of light
- Paraxial approximation
- Polarization (waves)
- Siae Microelettronica patent
References
- ↑ Willner, Alan E. (4 August 2016). "Twisted light could dramatically boost data rates: Orbital angular momentum could take optical and radio communication to new heights". IEEE Spectrum. https://spectrum.ieee.org/telecom/wireless/twisted-light-could-dramatically-boost-data-rates.
- ↑ Siegman, Anthony E. (1986). Lasers. University Science Books. pp. 1283. ISBN 978-0-935702-11-8. https://archive.org/details/lasers0000sieg.
- ↑ Belinfante, F. J. (1940). "On the current and the density of the electric charge, the energy, the linear momentum and the angular momentum of arbitrary fields". Physica 7 (5): 449–474. doi:10.1016/S0031-8914(40)90091-X. Bibcode: 1940Phy.....7..449B.
- ↑ Humblet, J. (1943). "Sur le moment d'impulsion d'une onde electromagnetique". Physica 10 (7): 585–603. doi:10.1016/S0031-8914(43)90626-3. Bibcode: 1943Phy....10..585H.
- ↑ 5.0 5.1 Beijersbergen, M.W.; Coerwinkel, R.P.C.; Kristensen, M.; Woerdman, J.P. (December 1994). "Helical-wavefront laser beams produced with a spiral phaseplate". Optics Communications 112 (5–6): 321–327. doi:10.1016/0030-4018(94)90638-6. Bibcode: 1994OptCo.112..321B.
- ↑ Bazhenov, V.Yu.; Soskin, M.S.; Vasnetsov, M.V. (May 1992). "Screw Dislocations in Light Wavefronts". Journal of Modern Optics 39 (5): 985–990. doi:10.1080/09500349214551011. Bibcode: 1992JMOp...39..985B.
- ↑ Williams, M.D.; Coles, M.M.; Bradshaw, D.S.; Andrews, D.L. (March 2014). "Direct generation of optical vortices". Physical Review A 89 (3): 033837. doi:10.1103/PhysRevA.89.033837. Bibcode: 2014PhRvA..89c3837W. https://ueaeprints.uea.ac.uk/56744/1/PRA_twisted.pdf.
- ↑ Kang, Ming; Chen, Jing; Wang, Xi-Lin; Wang, Hui-Tian (2012-03-06). "Twisted Vector Field from an Inhomogeneous and Anisotropic Metamaterial". Journal of the Optical Society of America B 29 (4): 572–576. doi:10.1364/JOSAB.29.000572. Bibcode: 2012JOSAB..29..572K.
- ↑ Bouchard, Frederic; Leon, Israel De; Schulz, Sebastian A.; Upham, Jeremy; Karimi, Ebrahim; Boyd, Robert W. (2014-09-11). "Optical Spin-to-Orbital Angular Momentum Conversion in Ultra-Thin Metasurfaces with Arbitrary Topological Charges". Appl. Phys. Lett. 105 (10): 101905. doi:10.1063/1.4895620. Bibcode: 2014ApPhL.105j1905B.
- ↑ Chen, Menglin L. N.; Jiang, Li Jun; Sha, Wei E. I. (2016-11-08). "Ultrathin Complementary Metasurface for Orbital Angular Momentum Generation at Microwave Frequencies". IEEE Trans. Antennas Propag. 65 (1): 396–400. doi:10.1109/TAP.2016.2626722. Bibcode: 2017ITAP...65..396C.
- ↑ Chen, Menglin L. N.; Jiang, Li Jun; Sha, Wei E. I. (2016-02-11). "Artificial Perfect Electric Conductor-Perfect Magnetic Conductor Anisotropic Metasurface for Generating Orbital Angular Momentum of Microwave with Nearly Perfect Conversion Efficiency". J. Appl. Phys. 119 (6): 064506. doi:10.1063/1.4941696. Bibcode: 2016JAP...119f4506C.
- ↑ Cai, Xinlun; Wang, Jianwei; Strain, Michael J.; Johnson-Morris, Benjamin; Zhu, Jiangbo; Sorel, Marc; O’Brien, Jeremy L.; Thompson, Mark G. et al. (2012-10-19). "Integrated Compact Optical Vortex Beam Emitters" (in en). Science 338 (6105): 363–366. doi:10.1126/science.1226528. ISSN 0036-8075. PMID 23087243. Bibcode: 2012Sci...338..363C. https://www.science.org/doi/10.1126/science.1226528.
- ↑ Zhou, Nan; Zheng, Shuang; Cao, Xiaoping; Zhao, Yifan; Gao, Shengqian; Zhu, Yuntao; He, Mingbo; Cai, Xinlun et al. (2019-05-03). "Ultra-compact broadband polarization diversity orbital angular momentum generator with 3.6 × 3.6 μm 2 footprint" (in en). Science Advances 5 (5): eaau9593. doi:10.1126/sciadv.aau9593. ISSN 2375-2548. PMID 31172022. Bibcode: 2019SciA....5.9593Z.
- ↑ Zhang, Zhifeng; Zhao, Haoqi; Pires, Danilo Gomes; Qiao, Xingdu; Gao, Zihe; Jornet, Josep M.; Longhi, Stefano; Litchinitser, Natalia M. et al. (2020-10-21). "Ultrafast control of fractional orbital angular momentum of microlaser emissions" (in en). Light: Science & Applications 9 (1): 179. doi:10.1038/s41377-020-00415-3. ISSN 2047-7538. PMID 33101659. Bibcode: 2020LSA.....9..179Z.
- ↑ Zhao, Han; Qiao, Xingdu; Wu, Tianwei; Midya, Bikashkali; Longhi, Stefano; Feng, Liang (2019-09-13). "Non-Hermitian topological light steering" (in en). Science 365 (6458): 1163–1166. doi:10.1126/science.aay1064. ISSN 0036-8075. PMID 31515392. Bibcode: 2019Sci...365.1163Z.
- ↑ He, Tiantian; Meng, Yuan; Liu, Zhoutian; Hu, Futai; Wang, Rui; Li, Dan; Yan, Ping; Liu, Qiang et al. (2021-11-22). "Guided mode meta-optics: metasurface-dressed waveguides for arbitrary mode couplers and on-chip OAM emitters with a configurable topological charge" (in en). Optics Express 29 (24): 39406–39418. doi:10.1364/OE.443186. ISSN 1094-4087. PMID 34809306. Bibcode: 2021OExpr..2939406H. https://opg.optica.org/abstract.cfm?URI=oe-29-24-39406.
- ↑ Meng, Yuan; Chen, Yizhen; Lu, Longhui; Ding, Yimin; Cusano, Andrea; Fan, Jonathan A.; Hu, Qiaomu; Wang, Kaiyuan et al. (2021-11-22). "Optical meta-waveguides for integrated photonics and beyond" (in en). Light: Science & Applications 10 (1): 235. doi:10.1038/s41377-021-00655-x. ISSN 2047-7538. PMID 34811345. Bibcode: 2021LSA....10..235M.
- ↑ "'Twisted light' carries 2.5 terabits of data per second". BBC. 25 June 2012. https://www.bbc.co.uk/news/science-environment-18551284.
- ↑ Yuan, Shuai S. A.; Wu, Jie; Chen, Menglin L. N.; Lan, Zhihao; Zhang, Liang; Sun, Sheng; Huang, Zhixiang; Chen, Xiaoming et al. (16 December 2021). "Approaching the Fundamental Limit of Orbital-Angular-Momentum Multiplexing Through a Hologram Metasurface". Physical Review Applied 16 (6): 064042. doi:10.1103/PhysRevApplied.16.064042. Bibcode: 2021PhRvP..16f4042Y.
- ↑ Padgett, [ed.:] L. Allen, Stephen M. Barnett, Miles J. (2003). Optical angular momentum. Bristol [u.a.]: Institute of Physics Publ.. ISBN 978-0-7503-0901-1.
- ↑ Ruffato, Gianluca; Massari, Michele; Romanato, Filippo (20 April 2016). "Diffractive optics for combined spatial- and mode- division demultiplexing of optical vortices: design, fabrication and optical characterization". Scientific Reports 6 (1): 24760. doi:10.1038/srep24760. PMID 27094324. Bibcode: 2016NatSR...624760R.
- ↑ Zhang, Wuhong; Qi, Qianqian; Zhou, Jie; Chen, Lixiang (14 April 2014). "Mimicking Faraday Rotation to Sort the Orbital Angular Momentum of Light". Physical Review Letters 112 (15): 153601. doi:10.1103/PhysRevLett.112.153601. PMID 24785038. Bibcode: 2014PhRvL.112o3601Z.
- ↑ Berkhout, Gregorius C. G.; Lavery, Martin P. J.; Courtial, Johannes; Beijersbergen, Marco W.; Padgett, Miles J. (4 October 2010). "Efficient Sorting of Orbital Angular Momentum States of Light". Physical Review Letters 105 (15): 153601. doi:10.1103/PhysRevLett.105.153601. PMID 21230900. Bibcode: 2010PhRvL.105o3601B.
- ↑ Ruffato, Gianluca; Massari, Michele; Parisi, Giuseppe; Romanato, Filippo (3 April 2017). "Test of mode-division multiplexing and demultiplexing in free-space with diffractive transformation optics". Optics Express 25 (7): 7859–7868. doi:10.1364/OE.25.007859. PMID 28380904. Bibcode: 2017OExpr..25.7859R.
- ↑ Wen, Yuanhui; Chremmos, Ioannis; Chen, Yujie; Zhu, Jiangbo; Zhang, Yanfeng; Yu, Siyuan (11 May 2018). "Spiral Transformation for High-Resolution and Efficient Sorting of Optical Vortex Modes". Physical Review Letters 120 (19): 193904. doi:10.1103/PhysRevLett.120.193904. PMID 29799240. Bibcode: 2018PhRvL.120s3904W.
- ↑ Joseph, S.K.; Chew, L. Y.; M.A. F., Sanjuan (10 Nov 2015). "Effect of geometry on the classical entanglement in a chaotic optical fiber". Optics Express 23 (25): 32191–32201. doi:10.1364/OE.23.032191. PMID 26699009. Bibcode: 2015OExpr..2332191J. https://www.osapublishing.org/oe/fulltext.cfm?uri=oe-23-25-32191&id=333200.
- ↑ Pecoraro, A.; Cardano, F.; Marrucci, L.; Porzio, A. (2019-07-15). "Continuous-variable entangled states of light carrying orbital angular momentum" (in en). Physical Review A 100 (1): 012321. doi:10.1103/PhysRevA.100.012321. ISSN 2469-9926. Bibcode: 2019PhRvA.100a2321P. https://link.aps.org/doi/10.1103/PhysRevA.100.012321.
- ↑ Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. (2001). "Entanglement of the orbital angular momentum states of photons". Nature 412 (6844): 313–316. doi:10.1038/35085529. PMID 11460157. Bibcode: 2001Natur.412..313M.
- ↑ Walborn, S.P.; Oliveira, A.N.; Thebaldi, R.S.; Monken, C.H. (2004). "Entanglement and conservation of orbital angular momentum in spontaneous parametric down-conversion". Physical Review A 69 (2): 023811. doi:10.1103/PhysRevA.69.023811. Bibcode: 2004PhRvA..69b3811W.
- ↑ Jack, B.; Yao, A. M.; Leach, J.; Romero, J.; Franke-Arnold, S.; Ireland, D. G.; Barnett, S. M.; Padgett, M. J. (30 April 2010). "Entanglement of arbitrary superpositions of modes within two-dimensional orbital angular momentum state spaces". Physical Review A 81 (4): 043844. doi:10.1103/PhysRevA.81.043844. Bibcode: 2010PhRvA..81d3844J. https://espace.library.uq.edu.au/view/UQ:409754/UQ409754_OA.pdf.
- ↑ Mirhosseini, Mohammad; Magaña-Loaiza, Omar S.; O'Sullivan, Malcolm N.; Rodenburg, Brandon; Malik, Mehul; Lavery, Martin P. J.; Padgett, Miles J.; Gauthier, Daniel J. et al. (20 March 2015). "High-dimensional quantum cryptography with twisted light". New Journal of Physics 17 (3): 033033. doi:10.1088/1367-2630/17/3/033033. Bibcode: 2015NJPh...17c3033M.
- ↑ Tamburini, Fabrizio; Thidé, Bo; Della Valle, Massimo (February 2020). "Measurement of the spin of the M87 black hole from its observed twisted light". Monthly Notices of the Royal Astronomical Society: Letters 492 (1): L22–L27. doi:10.1093/mnrasl/slz176. Bibcode: 2020MNRAS.492L..22T.
External links
- Allen, L.; Barnett, Stephen M.; Padgett, Miles J. (2003). Optical Angular Momentum. Bristol: Institute of Physics. ISBN 978-0-7503-0901-1..
- Torres, Juan P.; Torner, Lluis (2011). Twisted Photons: Applications of Light with Orbital Angular Momentum. Bristol: Wiley-VCH. ISBN 978-3-527-40907-5..
- Andrews, David L.; Babiker, Mohamed (2012). The Angular Momentum of Light. Cambridge: Cambridge University Press. pp. 448. ISBN 9781107006348. http://www.cambridge.org/de/knowledge/isbn/item6687744/The%20Angular%20Momentum%20of%20Light/.
- Glasgow Optics Group
- Leiden Institute of Physics
- ICFO
- Università Di Napoli "Federico II" (Archived copy)
- Università Di Roma "La Sapienza"
- University of Ottawa
- Elementary demonstration using a laser pointer
 |