Physics:Physics of optical holography

Short description: Overview article

Optical holography is a technique which enables an optical wavefront to be recorded and later re-constructed. Holography is best known as a method of generating three-dimensional images but it also has a wide range of other applications.

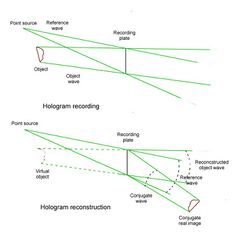
A hologram is made by superimposing a second wavefront (normally called the reference beam) on the wavefront of interest, thereby generating an interference pattern which is recorded on a physical medium. When only the second wavefront illuminates the interference pattern, it is diffracted to recreate the original wavefront. Holograms can also be computer-generated by modelling the two wavefronts and adding them together digitally. The resulting digital image is then printed it onto a suitable mask or film and illuminated by a suitable source to reconstruct the wavefront of interest.

Basic physics

To understand the process, it is helpful to understand interference and diffraction. Interference occurs when one or more wavefronts are superimposed. Diffraction occurs when a wavefront encounters an object. The process of producing a holographic reconstruction is explained below purely in terms of interference and diffraction. It is somewhat simplified but is accurate enough to give an understanding of how the holographic process works.

For those unfamiliar with these concepts, it is worthwhile to read those articles before reading further in this article.

A simple hologram can be made by superimposing two plane waves from the same light source on a light recording medium such as a photographic emulsion. The two waves interfere, giving a straight-line fringe pattern whose intensity varies sinusoidally across the medium. The spacing of the fringe pattern is determined by the angle between the two waves, and by the wavelength of the light.

The recorded light pattern is a diffraction grating, which is a structure with a repeating pattern. A simple example is a metal plate with slits cut at regular intervals. A light wave that is incident on a grating is split into several waves; the direction of these diffracted waves is determined by the grating spacing and the wavelength of the light.

When the recorded light pattern is illuminated by only one of the plane waves used to create it, it can be shown that one of the diffracted waves is a re-construction of the other plane wave.

Interference between a point source and a plane wave, both incident normally on the plate

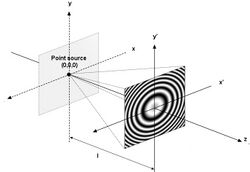
When a plane wave is added to a point source and the resulting interference pattern recorded, a point source hologram is produced. This is effectively a Fresnel zone plate which acts as a lens. If the plane wave is normally incident on the recording plate, three waves are diffracted by the plate

the original plane wave

a wave which appears to diverge from the point source - this is a reconstruction of the original point source wave

a wave which is focused to a point on the other side of the plate at the same distance as the original point source

This is known as an in-line hologram. Its usefulness is limited by the fact that all three waves are superimposed.

If the plane wave illuminates the recording plate at non-normal incidence, then the three diffracted waves are now as follows:

the original plane wave

a wave which appears to diverge from the original point source - this is the re-constructed wave

a wave which converges to a point which is deflected from the normal by twice the angle of incidence of the plane wave - this is known as the conjugate wave.

The three waves are now separated in space. This is known as an off-axis hologram. It was first developed by Leith and Upatnieks and was a vital step in enabling 3-d images to be produced with holography.

Theory underlying the holographic process

General form

The complex amplitude of a monochromatic electromagnetic wave can be represented by

[math]\displaystyle{ \mathbf{U}(\mathbf{r}) = A \exp{i [\varphi(\mathbf{r})]} }[/math]

where A represents the amplitude of the vector, and [math]\displaystyle{ \varphi (\mathbf{r}) }[/math] its phase.

To make a hologram, two waves are added together to give a total complex amplitude which can be represented as

[math]\displaystyle{ \mathbf{U}_\text{T} = \mathbf{U}_\text{R} + \mathbf{U}_\text{O} = A_\text{R} \exp {i (\varphi_\text{R})} + A_\text{O} \exp {i( \varphi_\text{O})} }[/math]

where R refers to the recording wavefront, known as the reference wavefront, and O refer to the wavefront being recorded. The dependence on r has been omitted for clarity.

The intensity of the combined beams is the average value of the complex amplitude times its complex conjugate:

[math]\displaystyle{ \mathbf{I}_T = \left\langle\mathbf{U}_\text{T} \mathbf{U}_\text{T}^*\right\rangle = A_\text{R}^2 + A_\text{O}^2 + A_\text{R}A_\text{O} \exp{i(\varphi_\text{R} - \varphi_\text{O})} + A_\text{R}A_\text{O} \exp{-i(\varphi_\text{R}- \varphi_\text{O})} }[/math]

A recording medium is exposed to the two beams and then developed. Assume that the amplitude transmittance, [math]\displaystyle{ \mathbf{t} }[/math] of the developed photographic plate is linearly related to the intensity of the interference pattern.

[math]\displaystyle{ \mathbf{t} = \mathbf{t}_0 + \beta \left[ A_\text{R}^2 + A_\text{O}^2 + A_\text{R}A_\text{O} \exp{i(\varphi_\text{R} - \varphi_\text{O})} + A_\text{R}A_\text{O} \exp{-i(\varphi_\text{R} - \varphi_\text{O})}\right] }[/math]

where [math]\displaystyle{ \mathbf{t}_0 }[/math] is a constant background transmittance and [math]\displaystyle{ \beta }[/math] is constant,

When the developed photographic plate is illuminated only by the reference beam, [math]\displaystyle{ \mathbf{U_R} }[/math], the amplitude of the light transmitted through the plate, U_H, is given by

[math]\displaystyle{ \mathbf{U}_H = \mathbf{t} A_\text{R} \exp {i \varphi_\text{R}} = \left[ \mathbf{t}_0 + \beta \left[ A_\text{R}^2 + A_\text{O}^2 + A_\text{R}A_\text{O} \exp {i (\varphi_\text{R} - \varphi_\text{O})} + A_\text{R}A_\text{O} \exp{-i (\varphi_\text{R} - \varphi_\text{O})}\right]\right] A_\text{R} \exp {i \varphi_\text{R}} }[/math]

This can be split into three terms:

[math]\displaystyle{ \begin{align} \mathbf{U}_1 &= \left[\mathbf{t}_0 + \beta A_\text{R}^2 + \beta A_\text{O}^2\right] A_\text{R} \exp {i \varphi_\text{R}} \\ \mathbf{U}_2 &= \beta A_\text{R}^2 A_\text{O} \exp i\varphi _\text{O} \\ \mathbf{U}_3 &= \beta A_\text{R}^2 A_\text{O} \exp{i (2 \varphi_\text{R}- \varphi_\text{O})} \end{align} }[/math]

[math]\displaystyle{ \mathbf{U}_1 }[/math] is a modified version of the reference wave. The first term is a reduced amplitude version, the second is also a reduced amplitude version if the reference wave amplitude is uniform. The third term produces a halo round the transmitted reference wave which is negligible when the amplitude of the object wave is much less than that of the reference wave

[math]\displaystyle{ \mathbf{U}_2 }[/math] is the reconstructed object wave which is identical to the original wave except that its amplitude is reduced. When the object wave is generated by light scattered from an object or objects, a virtual image of the object(s) is formed when a lens is placed in the reconstructed wave.

[math]\displaystyle{ \mathbf{U}_3 }[/math] is known as the conjugate wave. It is similar to the object wave but has the opposite curvature. When the object wave is generated by light scattered from an object or a series of objects, a real image is formed on the opposite side of the hologram plate to where the object was located and is deflected from the normal axis by twice the angle between the reference wave and the normal direction.

Two plane waves

Interference fringes in overlapping plane waves

The reference and object wave are monochromatic plane waves of uniform amplitude

[math]\displaystyle{ \begin{align} \mathbf{U_\text{R}}(\mathbf{r}) &= A _\text{R} \exp\left[i \mathbf{k_\text{R}} \cdot \mathbf{r}\right] \\ \mathbf{U_\text{O}}(\mathbf{r}) &= A _\text{O} \exp\left[i \mathbf{k_\text{O}} \cdot \mathbf{r}\right] \end{align} }[/math]

where the vectors [math]\displaystyle{ \mathbf{k} }[/math] are related to the unit vectors [math]\displaystyle{ \mathbf{n} }[/math] which define the direction of travel and the wavelength [math]\displaystyle{ \lambda }[/math] of the two waves by

[math]\displaystyle{ \mathbf{k} = 2\pi \frac{\mathbf{n}}{\lambda} }[/math]

The expression for [math]\displaystyle{ \mathbf t }[/math] in the previous section can be written as

[math]\displaystyle{ \mathbf{t} = \mathbf{t}_0 + \beta \left[ A_\text{O}^2 + A_\text{R}^2+ A_\text{O}A_\text{R} \cos { \left([\mathbf{k_O} - \mathbf{k_R}] \cdot \mathbf{r}\right)}\right] }[/math]

from which it can be seen that the transmission of the holographic recording varies sinusoidally, i.e.it is a diffraction grating, where spacing of the fringes depends on the angle between the two waves and the orientation of the holographic plate.

The reconstructed wave is:

[math]\displaystyle{ \mathbf{U}_2 = \beta A_\text{R}^2 A_\text{O} \exp i (\mathbf{k}_O \cdot \mathbf{r}) }[/math]

which is a plane wave travelling in the direction [math]\displaystyle{ \mathbf{k} _O }[/math], i.e. it is the reconstructed object wave with a modified amplitude.

The conjugate wave is:

[math]\displaystyle{ \mathbf{U}_3 = A_\text{O}A_\text{R} \exp[i (2 \mathbf{k}_R - \mathbf{k}_O) \cdot \mathbf{r}] }[/math]

which is a plane wave travelling in the direction [math]\displaystyle{ 2\mathbf{k} _R - \mathbf{k} _O }[/math]

This shows that the transmission of the photographic plate varies sinusoidally so it acts as a diffraction grating. If one of the waves is normally incident to the hologram plate, and the other is incident at an angle [math]\displaystyle{ \theta }[/math], the spacing of the fringes is [math]\displaystyle{ d = \lambda / \sin {\theta} }[/math] and the first order diffracted waves will be at angles given by [math]\displaystyle{ \sin {\gamma} = \pm \lambda / d = \sin {\theta} }[/math]. One of these is the reconstructed object plane wave, the other is the conjugate wave.

Plane wave and point source

Interference pattern generated by a point source and plane waves incident at various angles

Consider a point source located at the origin which illuminates a photographic plate which is located at a distance [math]\displaystyle{ l }[/math] normal to the z axis. The phase difference between the source and a point (x, y, z) is given approximately by

[math]\displaystyle{ \phi_O = \frac {\pi r^2}{\lambda l} }[/math]

where [math]\displaystyle{ r = \sqrt{x^2 + y^2} }[/math]

The complex amplitude of the object beam is then given by

[math]\displaystyle{ \mathbf{U_O} = A_0 \exp i{\frac {\pi r^2}{\lambda l}} }[/math].

The form of the interference pattern for various directions of incidence for the reference wave are shown on the right.

The reference plane wave is

[math]\displaystyle{ \mathbf{U _\text{R}}(\mathbf{r}) = A _\text{R} \exp[i \mathbf{k _\text{R}} \cdot \mathbf{r}] }[/math]

The reconstructed wave is described by the second term:

[math]\displaystyle{ \mathbf{U}_2 = \beta A_\text{R}^2 A_\text{O} \exp i\frac {\pi r^2}{\lambda l} }[/math]

The conjugate wave is described by the third term

[math]\displaystyle{ \mathbf{U}_3 = A_\text{O}A_\text{R} \exp i \left(\mathbf{k _\text{R}} \cdot \mathbf{r}-{\frac {\pi r^2}{\lambda l}} \right) }[/math]

It emerges at twice the angle between the object and references wave and converges to a point which is at the same distance from the plate as the original point source.

General object and a point source

Set up for making and replaying a hologram

When light is scattered off a general object, the amplitude of the scattered light at any point [math]\displaystyle{ (\mathbf{r}) }[/math] can be represented by

[math]\displaystyle{ \mathbf{U_\text{O}}(\mathbf{r}) = A_\text{O} (\mathbf{r}) \exp{i [\varphi _\text{O}(\mathbf{r})]} }[/math]

where both the phase and the amplitude vary with [math]\displaystyle{ \mathbf{r} }[/math].

The distance travelled by a wave emitted from a point source located at a point [math]\displaystyle{ \mathbf{r}_\text{R} }[/math] to a point [math]\displaystyle{ \mathbf{r} }[/math] travels a distance [math]\displaystyle{ \mathbf{r} - \mathbf{r}_\text{R} }[/math], so that the phase change is [math]\displaystyle{ \phi_\text{R} = \frac {2 \pi (\mathbf{r} - \mathbf{r}_\text{R})}{\lambda} }[/math] so that its amplitude is given by

[math]\displaystyle{ \mathbf{U}_\text{R}(\mathbf{r}) = A_\text{R} \exp{ \frac {2 \pi i (\mathbf{r} - \mathbf{r}_\text{R})}{\lambda}} }[/math]

where [math]\displaystyle{ A_\text{R} }[/math] is constant.

The reconstructed object wave is

[math]\displaystyle{ \mathbf{U}_2 = \beta A_\text{R}^2 A_\text{O}(\mathbf{r}) \exp{i [\varphi _\text{O}(\mathbf{r})]} }[/math]

The conjugate wave is given by

[math]\displaystyle{ \mathbf{U}_3 = \beta A_\text{R} \exp { \frac {4 \pi i (\mathbf{r} - \mathbf{r}_\text{R})}{\lambda}} A_\text{O} (\mathbf{r}) \exp{i \varphi _\text{O}(\mathbf{r})} }[/math]

Recording a hologram

Items required

Making a hologram

To make a hologram, the following are required:

• a suitable object or set of objects
• part of the laser beam to be directed so that it illuminates the object (the object beam) and another part so that it illuminates the recording medium directly (the reference beam), enabling the reference beam and the light which is scattered from the object onto the recording medium to form an interference pattern
• a recording medium which converts this interference pattern into an optical element which modifies either the amplitude or the phase of an incident light beam according to the intensity of the interference pattern.
• a laser beam that produces coherent light with one wavelength.
• an environment which provides sufficient mechanical and thermal stability that the interference pattern is stable during the time in which the interference pattern is recorded.

These requirements are inter-related, and it is essential to understand the nature of optical interference to see this. Interference is the variation in intensity which can occur when two light waves are superimposed. The intensity of the maxima exceeds the sum of the individual intensities of the two beams, and the intensity at the minima is less than this and may be zero. The interference pattern maps the relative phase between the two waves, and any change in the relative phases causes the interference pattern to move across the field of view. If the relative phase of the two waves changes by one cycle, then the pattern drifts by one whole fringe. One phase cycle corresponds to a change in the relative distances travelled by the two beams of one wavelength. Since the wavelength of light is of the order of 0.5 μm, it can be seen that very small changes in the optical paths travelled by either of the beams in the holographic recording system lead to movement of the interference pattern which is the holographic recording. Such changes can be caused by relative movements of any of the optical components or the object itself, and also by local changes in air-temperature. It is essential that any such changes are significantly less than the wavelength of light if a clear well-defined recording of the interference is to be created.

The exposure time required to record the hologram depends on the laser power available, on the particular medium used and on the size and nature of the object(s) to be recorded, just as in conventional photography. This determines the stability requirements. Exposure times of several minutes are typical when using quite powerful gas lasers and silver halide emulsions. All the elements within the optical system have to be stable to fractions of a μm over that period. It is possible to make holograms of much less stable objects by using a pulsed laser which produces a large amount of energy in a very short time (μs or less). These systems have been used to produce holograms of live people. A holographic portrait of Dennis Gabor was produced in 1971 using a pulsed ruby laser.

Thus, the laser power, recording medium sensitivity, recording time and mechanical and thermal stability requirements are all interlinked. Generally, the smaller the object, the more compact the optical layout, so that the stability requirements are significantly less than when making holograms of large objects.

Another very important laser parameter is its coherence. This can be envisaged by considering a laser producing a sine wave whose frequency drifts over time; the coherence length can then be considered to be the distance over which it maintains a single frequency. This is important because two waves of different frequencies do not produce a stable interference pattern. The coherence length of the laser determines the depth of field which can be recorded in the scene. A good holography laser will typically have a coherence length of several meters, ample for a deep hologram.

The objects that form the scene must, in general, have optically rough surfaces so that they scatter light over a wide range of angles. A specularly reflecting (or shiny) surface reflects the light in only one direction at each point on its surface, so in general, most of the light will not be incident on the recording medium. A hologram of a shiny object can be made by locating it very close to the recording plate.

Hologram classifications

There are three important properties of a hologram which are defined in this section. A given hologram will have one or other of each of these three properties, e.g. an amplitude modulated, thin, transmission hologram, or a phase modulated, volume, reflection hologram.

Amplitude and phase modulation holograms

An amplitude modulation hologram is one where the amplitude of light diffracted by the hologram is proportional to the intensity of the recorded light. A straightforward example of this is photographic emulsion on a transparent substrate. The emulsion is exposed to the interference pattern, and is subsequently developed giving a transmittance which varies with the intensity of the pattern – the more light that fell on the plate at a given point, the darker the developed plate at that point.

A phase hologram is made by changing either the thickness or the refractive index of the material in proportion to the intensity of the holographic interference pattern. This is a phase grating and it can be shown that when such a plate is illuminated by the original reference beam, it reconstructs the original object wavefront. The efficiency (i.e., the fraction of the illuminated object beam which is converted into the reconstructed object beam) is greater for phase than for amplitude modulated holograms.

Thin holograms and thick (volume) holograms

A thin hologram is one where the thickness of the recording medium is much less than the spacing of the interference fringes which make up the holographic recording. The thickness of a thin hologram can be down to 60 nm by using a topological insulator material Sb₂Te₃ thin film. Ultrathin holograms hold the potential to be integrated with everyday consumer electronics like smartphones.

A thick or volume hologram is one where the thickness of the recording medium is greater than the spacing of the interference pattern. The recorded hologram is now a three dimensional structure, and it can be shown that incident light is diffracted by the grating only at a particular angle, known as the Bragg angle. If the hologram is illuminated with a light source incident at the original reference beam angle but a broad spectrum of wavelengths; reconstruction occurs only at the wavelength of the original laser used. If the angle of illumination is changed, reconstruction will occur at a different wavelength and the colour of the re-constructed scene changes. A volume hologram effectively acts as a colour filter.

Transmission and reflection holograms

A transmission hologram is one where the object and reference beams are incident on the recording medium from the same side. In practice, several more mirrors may be used to direct the beams in the required directions.

Normally, transmission holograms can only be reconstructed using a laser or a quasi-monochromatic source, but a particular type of transmission hologram, known as a rainbow hologram, can be viewed with white light.

In a reflection hologram, the object and reference beams are incident on the plate from opposite sides of the plate. The reconstructed object is then viewed from the same side of the plate as that at which the re-constructing beam is incident.

Only volume holograms can be used to make reflection holograms, as only a very low intensity diffracted beam would be reflected by a thin hologram.

Examples of full-color reflection holograms of mineral specimens:

• 

  Hologram of Elbaite on Quartz

• 

  Hologram of Tanzanite on Matrix

• 

  Hologram of Tourmaline on Quartz

• 

  Hologram of Amethyst on Quartz

Holographic recording media

The recording medium has to convert the original interference pattern into an optical element that modifies either the amplitude or the phase of an incident light beam in proportion to the intensity of the original light field.

The recording medium should be able to resolve fully all the fringes arising from interference between object and reference beam. These fringe spacings can range from tens of micrometers to less than one micrometer, i.e. spatial frequencies ranging from a few hundred to several thousand cycles/mm, and ideally, the recording medium should have a response which is flat over this range. Photographic film has a very low or even zero response at the frequencies involved and cannot be used to make a hologram – for example, the resolution of Kodak's professional black and white film starts falling off at 20 lines/mm – it is unlikely that any reconstructed beam could be obtained using this film.

If the response is not flat over the range of spatial frequencies in the interference pattern, then the resolution of the reconstructed image may also be degraded.,

The table below shows the principal materials used for holographic recording. Note that these do not include the materials used in the mass replication of an existing hologram, which are discussed in the next section. The resolution limit given in the table indicates the maximal number of interference lines/mm of the gratings. The required exposure, expressed as millijoules (mJ) of photon energy impacting the surface area, is for a long exposure time. Short exposure times (less than ​¹⁄₁₀₀₀ of a second, such as with a pulsed laser) require much higher exposure energies, due to reciprocity failure.

General properties of recording materials for holography,

Material	Reusable	Processing	Type	Theoretical max. efficiency	Required exposure (mJ/cm2)	Resolution limit (mm−1)
Photographic emulsions	No	Wet	Amplitude	6%	1.5	5000
			Phase (bleached)	60%
Dichromated gelatin	No	Wet	Phase	100%	100	10,000
Photoresists	No	Wet	Phase	30%	100	3,000
Photothermoplastics	Yes	Charge and heat	Phase	33%	0.1	500–1,200
Photopolymers	No	Post exposure	Phase	100%	10000	5,000
Photorefractives	Yes	None	Phase	100%	10	10,000

Copying and mass production

An existing hologram can be copied by embossing or optically.

Most holographic recordings (e.g. bleached silver halide, photoresist, and photopolymers) have surface relief patterns which conform with the original illumination intensity. Embossing, which is similar to the method used to stamp out plastic discs from a master in audio recording, involves copying this surface relief pattern by impressing it onto another material.

The first step in the embossing process is to make a stamper by electrodeposition of nickel on the relief image recorded on the photoresist or photothermoplastic. When the nickel layer is thick enough, it is separated from the master hologram and mounted on a metal backing plate. The material used to make embossed copies consists of a polyester base film, a resin separation layer and a thermoplastic film constituting the holographic layer.

The embossing process can be carried out with a simple heated press. The bottom layer of the duplicating film (the thermoplastic layer) is heated above its softening point and pressed against the stamper, so that it takes up its shape. This shape is retained when the film is cooled and removed from the press. In order to permit the viewing of embossed holograms in reflection, an additional reflecting layer of aluminum is usually added on the hologram recording layer. This method is particularly suited to mass production.

The first book to feature a hologram on the front cover was The Skook (Warner Books, 1984) by JP Miller, featuring an illustration by Miller. The first record album cover to have a hologram was "UB44", produced in 1982 for the British group UB40 by Advanced Holographics in Loughborough. This featured a 5.75 inch square embossed hologram showing a 3D image of the letters UB carved out of polystyrene to look like stone and the numbers 44 hovering in space on the picture plane. On the inner sleeve was an explanation of the holographic process and instructions on how to light the hologram. National Geographic published the first magazine with a hologram cover in March 1984. Embossed holograms are used widely on credit cards, banknotes, and high value products for authentication purposes.

It is possible to print holograms directly into steel using a sheet explosive charge to create the required surface relief. The Royal Canadian Mint produces holographic gold and silver coinage through a complex stamping process.

A hologram can be copied optically by illuminating it with a laser beam, and locating a second hologram plate so that it is illuminated both by the reconstructed object beam, and the illuminating beam. Stability and coherence requirements are significantly reduced if the two plates are located very close together. An index matching fluid is often used between the plates to minimize spurious interference between the plates. Uniform illumination can be obtained by scanning point-by-point or with a beam shaped into a thin line.

Reconstructing and viewing the holographic image

Holographic self-portrait, exhibited at the National Polytechnic Museum, Sofia

When the hologram plate is illuminated by a laser beam identical to the reference beam which was used to record the hologram, an exact reconstruction of the original object wavefront is obtained. An imaging system (an eye or a camera) located in the reconstructed beam 'sees' exactly the same scene as it would have done when viewing the original. When the lens is moved, the image changes in the same way as it would have done when the object was in place. If several objects were present when the hologram was recorded, the reconstructed objects move relative to one another, i.e. exhibit parallax, in the same way as the original objects would have done. It was very common in the early days of holography to use a chess board as the object and then take photographs at several different angles using the reconstructed light to show how the relative positions of the chess pieces appeared to change.

A holographic image can also be obtained using a different laser beam configuration to the original recording object beam, but the reconstructed image will not match the original exactly. When a laser is used to reconstruct the hologram, the image is speckled just as the original image will have been. This can be a major drawback in viewing a hologram.

White light consists of light of a wide range of wavelengths. Normally, if a hologram is illuminated by a white light source, each wavelength can be considered to generate its own holographic reconstruction, and these will vary in size, angle, and distance. These will be superimposed, and the summed image will wipe out any information about the original scene, as if superimposing a set of photographs of the same object of different sizes and orientations. However, a holographic image can be obtained using white light in specific circumstances, e.g. with volume holograms and rainbow holograms. The white light source used to view these holograms should always approximate to a point source, i.e. a spot light or the sun. An extended source (e.g. a fluorescent lamp) will not reconstruct a hologram since its light is incident at each point at a wide range of angles, giving multiple reconstructions which will "wipe" one another out.

White light reconstructions do not contain speckles.

Volume holograms

A reflection-type volume hologram can give an acceptably clear reconstructed image using a white light source, as the hologram structure itself effectively filters out light of wavelengths outside a relatively narrow range. In theory, the result should be an image of approximately the same colour as the laser light used to make the hologram. In practice, with recording media that require chemical processing, there is typically a compaction of the structure due to the processing and a consequent colour shift to a shorter wavelength. Such a hologram recorded in a silver halide gelatin emulsion by red laser light will usually display a green image. Deliberate temporary alteration of the emulsion thickness before exposure, or permanent alteration after processing, has been used by artists to produce unusual colours and multicoloured effects.

Rainbow holograms

Rainbow hologram showing the change in colour in the vertical direction

In this method, parallax in the vertical plane is sacrificed to allow a bright, well-defined, gradiently colored reconstructed image to be obtained using white light. The rainbow holography recording process usually begins with a standard transmission hologram and copies it using a horizontal slit to eliminate vertical parallax in the output image. The viewer is therefore effectively viewing the holographic image through a narrow horizontal slit, but the slit has been expanded into a window by the same dispersion that would otherwise smear the entire image. Horizontal parallax information is preserved but movement in the vertical direction results in a color shift rather than altered vertical perspective. Because perspective effects are reproduced along one axis only, the subject will appear variously stretched or squashed when the hologram is not viewed at an optimum distance; this distortion may go unnoticed when there is not much depth, but can be severe when the distance of the subject from the plane of the hologram is very substantial. Stereopsis and horizontal motion parallax, two relatively powerful cues to depth, are preserved.

The holograms found on credit cards are examples of rainbow holograms. These are technically transmission holograms mounted onto a reflective surface like a metalized polyethylene terephthalate substrate commonly known as PET.

Fidelity of the reconstructed beam

Reconstructions from two parts of a broken hologram. Note the different viewpoints required to see the whole object

To replicate the original object beam exactly, the reconstructing reference beam must be identical to the original reference beam and the recording medium must be able to fully resolve the interference pattern formed between the object and reference beams. Exact reconstruction is required in holographic interferometry, where the holographically reconstructed wavefront interferes with the wavefront coming from the actual object, giving a null fringe if there has been no movement of the object and mapping out the displacement if the object has moved. This requires very precise relocation of the developed holographic plate.

Any change in the shape, orientation or wavelength of the reference beam gives rise to aberrations in the reconstructed image. For instance, the reconstructed image is magnified if the laser used to reconstruct the hologram has a longer wavelength than the original laser. Nonetheless, good reconstruction is obtained using a laser of a different wavelength, quasi-monochromatic light or white light, in the right circumstances.

Since each point in the object illuminates all of the hologram, the whole object can be reconstructed from a small part of the hologram. Thus, a hologram can be broken up into small pieces and each one will enable the whole of the original object to be imaged. One does, however, lose information and the spatial resolution gets worse as the size of the hologram is decreased – the image becomes "fuzzier". The field of view is also reduced, and the viewer will have to change position to see different parts of the scene.