Physics:Polyakov loop

From HandWiki
Short description: Thermal Wilson loop

In quantum field theory, the Polyakov loop is the thermal analogue of the Wilson loop, acting as an order parameter for confinement in pure gauge theories at nonzero temperatures. In particular, it is a Wilson loop that winds around the compactified Euclidean temporal direction of a thermal quantum field theory. It indicates confinement because its vacuum expectation value must vanish in the confined phase due to its non-invariance under center gauge transformations. This also follows from the fact that the expectation value is related to the free energy of individual quarks, which diverges in this phase. Introduced by Alexander M. Polyakov in 1975,[1] they can also be used to study the potential between pairs of quarks at nonzero temperatures.

Definition

Thermal quantum field theory is formulated in Euclidean spacetime with a compactified imaginary temporal direction of length [math]\displaystyle{ \beta }[/math]. This length corresponds to the inverse temperature of the field [math]\displaystyle{ \beta \propto 1/T }[/math]. Compactification leads to a special class of topologically nontrivial Wilson loops that wind around the compact direction known as Polyakov loops.[2] In [math]\displaystyle{ \text{SU}(N) }[/math] theories a straight Polyakov loop on a spatial coordinate [math]\displaystyle{ \boldsymbol x }[/math] is given by

[math]\displaystyle{ \Phi(\boldsymbol x) = \frac{1}{N}\text{tr} \ \mathcal P \exp\bigg[\int_0^\beta dx_4 A_4(\boldsymbol x, x_f)\bigg], }[/math]

where [math]\displaystyle{ \mathcal P }[/math] is the path-ordering operator and [math]\displaystyle{ A_4 }[/math] is the Euclidean temporal component of the gauge field. In lattice field theory this operator is reformulated in terms of temporal link fields [math]\displaystyle{ U_4(\boldsymbol m, j) }[/math] at a spatial position [math]\displaystyle{ \boldsymbol m }[/math] as[3]

[math]\displaystyle{ \Phi(\boldsymbol m) = \frac{1}{N}\text{tr} \bigg[ \prod_{j=0}^{N_T-1} U_4(\boldsymbol m, j)\bigg]. }[/math]

The continuum limit of the lattice must be taken carefully to ensure that the compact direction has fixed extent. This is done by ensuring that the finite number of temporal lattice points [math]\displaystyle{ N_T }[/math] is such that [math]\displaystyle{ \beta = N_T a }[/math] is constant as the lattice spacing [math]\displaystyle{ a }[/math] goes to zero.

Order parameter

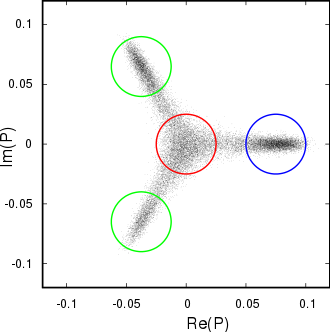
Two-dimensional scatter plot of the real and imaginary components of the expectation value of the Polyakov loop. Has many values clustered around the origin and around the three cubic roots of unity, corresponding to the expectation value in the confined and deconfined phase.
Scatter plot of the expectation value of the Polyakov line in a simulation of a [math]\displaystyle{ \text{SU}(3) }[/math] gauge theory around the confinement phase transition. The red circle denotes the confining phase, while the blue and green circles denote the nonzero expectation values in the deconfined phase. There are three clusters in the deconfined phase due to the [math]\displaystyle{ \mathbb Z_3 }[/math] group center of the gauge group.[4]

Gauge fields need to satisfy the periodicity condition [math]\displaystyle{ A_\mu(\boldsymbol x, x_4+\beta) = A_\mu(\boldsymbol x, x_4) }[/math] in the compactified direction. Meanwhile, gauge transformations only need to satisfy this up to a group center term [math]\displaystyle{ h }[/math] as [math]\displaystyle{ \Omega(\boldsymbol x, x_4+\beta) = h \Omega(\boldsymbol x, x_4) }[/math]. A change of basis can always diagonalize this so that [math]\displaystyle{ h=zI }[/math] for a complex number [math]\displaystyle{ z }[/math]. The Polyakov loop is topologically nontrivial in the temporal direction so unlike other Wilson loops it transforms as [math]\displaystyle{ \Phi(\boldsymbol x) \rightarrow z \Phi(\boldsymbol x) }[/math] under these transformations.[5] Since this makes the loop gauge dependent for [math]\displaystyle{ z \neq 1 }[/math], by Elitzur's theorem non-zero expectation values of [math]\displaystyle{ \langle \Phi\rangle }[/math] imply that the center group must be spontaneously broken, implying confinement in pure gauge theory. This makes the Polyakov loop an order parameter for confinement in thermal pure gauge theory, with a confining phase occurring when [math]\displaystyle{ \langle \Phi\rangle = 0 }[/math] and deconfining phase when [math]\displaystyle{ \langle \Phi\rangle \neq 0 }[/math].[6] For example, lattice calculations of quantum chromodynamics with infinitely heavy quarks that decouple from the theory shows that the deconfinement phase transition occurs at around a temperature of [math]\displaystyle{ 270 }[/math] MeV.[7] Meanwhile, in a gauge theory with quarks, these break the center group and so confinement must instead be deduced from the spectrum of asymptotic states, the color neutral hadrons.

For gauge theories that lack a nontrivial group center that could be broken in the confining phase, the Polyakov loop expectation values are nonzero even in this phase. They are however still a good indicator of confinement since they generally experience a sharp jump at the phase transition. This is the case for example in the Higgs model with the exceptional gauge group [math]\displaystyle{ G 2 }[/math].[8]

The Nambu–Jona-Lasinio model lacks local color symmetry and thus cannot capture the effects of confinement. However, Polyakov loops can be used to construct the Polyakov-loop-extended Nambu–Jona-Lasinio model which treats both the chiral condensate and the Polyakov loops as classical homogeneous fields that couple to quarks according to the symmetries and symmetry breaking patters of quantum chromodynamics.[9][10][11]

Quark free energy

The free energy [math]\displaystyle{ F }[/math] of [math]\displaystyle{ N }[/math] quarks and [math]\displaystyle{ \bar N }[/math] antiquarks, subtracting out the vacuum energy, is given in terms of the correlation functions of Polyakov loops[12]

[math]\displaystyle{ e^{-\beta F} = \langle \Phi(\boldsymbol x_1)\dots \Phi(\boldsymbol x_{N_q})\Phi^\dagger(\boldsymbol x'_1) \cdots \Phi^\dagger(\boldsymbol x_{\bar N}')\rangle. }[/math]

This free energy is another way to see that the Polyakov loop acts as an order parameter for confinement since the free energy of a single quark is given by [math]\displaystyle{ e^{-\beta \Delta F} = \langle \Phi(\boldsymbol x)\rangle }[/math].[13] Confinement of quarks means that it would take an infinite amount of energy to create a configuration with a single free quark, therefore its free energy must be infinite and so the Polyakov loop expectation value must vanish in this phase, in agreement with the center symmetry breaking argument.

The formula for the free energy can also be used to calculate the potential between a pair of infinitely massive quarks spatially separated by [math]\displaystyle{ r =|\boldsymbol x_1 - \boldsymbol x_2| }[/math]. Here the potential [math]\displaystyle{ V(r) }[/math] is the first term in the free energy, so that the correlation function of two Polyakov loops is

[math]\displaystyle{ \langle \Phi(\boldsymbol x_1)\Phi(\boldsymbol x_2)\rangle \propto e^{-\beta V(r)}(1+\mathcal O(e^{-\beta\Delta E(r)})), }[/math]

where [math]\displaystyle{ \Delta E }[/math] is the energy difference between the potential and the first excited state. In the confining phase the potential is linear [math]\displaystyle{ V(r) = \sigma r }[/math], where the constant of proportionality is known as the string tension. The string tension acquired from the Polyakov loop is always bounded from above by the string tension acquired from the Wilson loop.[14]

See also

References

  1. ↑ Polyakov, A.M. (1978). "Compact gauge fields and the infrared catastrophe". Physics Letters B 59 (1): 82–84. doi:10.1016/0370-2693(75)90162-8. https://dx.doi.org/10.1016/0370-2693%2875%2990162-8. 
  2. ↑ Wipf, A. (2021). "16". Statistical Approach to Quantum Field Theory (2 ed.). Springer. pp. 456–459. ISBN 978-3642331046. 
  3. ↑ Gattringer, C.; Lang, C.B. (2009). "3". Quantum Chromodynamics on the Lattice: An Introductory Presentation. Lecture Notes in Physics 788. Springer. pp. 57–58. doi:10.1007/978-3-642-01850-3. ISBN 978-3642018497. 
  4. ↑ Kovacs, T.G. (2021). "Localization at the quenched SU(3) phase transition". PoS LATTICE2021: 238. doi:10.22323/1.396.0238. 
  5. ↑ Bellwied, R.; Ratti, C. (2021). "2". The Deconfinement Transition of QCD. Springer. pp. 25–32. ISBN 978-3030672348. 
  6. ↑ Greensite, J. (2020). "4". An Introduction to the Confinement Problem (2 ed.). Springer. pp. 42–43. ISBN 978-3030515621. 
  7. ↑ Kogut, J.; Stephanov, M. (2003). "7". The Phases of Quantum Chromodynamics. Cambridge: Cambridge University Press. p. 178. ISBN 978-0521804509. 
  8. ↑ Holland, K. (2003). "Exceptional confinement in G(2) gauge theory". Nucl. Phys. B 668 (1–2): 207–236. doi:10.1016/S0550-3213(03)00571-6. Bibcode: 2003NuPhB.668..207H. 
  9. ↑ Friman, B. (2011). "4". The CBM Physics Book: Compressed Baryonic Matter in Laboratory Experiments. Springer. p. 239. ISBN 978-3642132926. 
  10. ↑ Ratti, C.; Thaler, M.A.; Weise, W. (2006). "Phases of QCD: Lattice thermodynamics and a field theoretical model". Phys. Rev. D 73 (1): 014019. doi:10.1103/PhysRevD.73.014019. Bibcode: 2006PhRvD..73a4019R. https://link.aps.org/doi/10.1103/PhysRevD.73.014019. 
  11. ↑ Roessner, S.; Ratti, C.; Weise, W. (2007). "Polyakov loop, diquarks, and the two-flavor phase diagram". Phys. Rev. D 75 (3): 034007. doi:10.1103/PhysRevD.75.034007. Bibcode: 2007PhRvD..75c4007R. https://link.aps.org/doi/10.1103/PhysRevD.75.034007. 
  12. ↑ McLarren, L.D.; Svetitsky, B. (1981). "Quark liberation at high temperature: A Monte Carlo study of SU(2) gauge theory". Phys. Rev. D 24 (2): 450–460. doi:10.1103/PhysRevD.24.450. Bibcode: 1981PhRvD..24..450M. https://link.aps.org/doi/10.1103/PhysRevD.24.450. 
  13. ↑ Makeenko, Y. (2002). "9". Methods of Contemporary Gauge Theory. Cambridge Monographs on Mathematical Physics. Cambridge: Cambridge University Press. pp. 168–169. doi:10.1017/CBO9780511535147. ISBN 978-0521809115. https://library.oapen.org/handle/20.500.12657/64018. 
  14. ↑ Borgs, C.; Seiler, E. (1983). "Lattice Yang-Mills theory at nonzero temperature and the confinement problem". Communications in Mathematical Physics 91 (3): 329–380. doi:10.1007/BF01208780. Bibcode: 1983CMaPh..91..329B. https://doi.org/10.1007/BF01208780. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Polyakov_loop&oldid=3280559"