Physics:Quantum ergodicity

From HandWiki
The eigenmode of a classically integrable system (e.g. the circular cavity on the left) can be very confined even for high mode number. On the contrary the eigenmodes of a classically chaotic system (e.g. the stadium-shaped cavity on the right) tend to become gradually more uniform with increasing mode number.

In quantum chaos, a branch of mathematical physics, quantum ergodicity is a property of the quantization of classical mechanical systems that are chaotic in the sense of exponential sensitivity to initial conditions. Quantum ergodicity states, roughly, that in the high-energy limit, the probability distributions associated to energy eigenstates of a quantized ergodic Hamiltonian tend to a uniform distribution in the classical phase space. This is consistent with the intuition that the flows of ergodic systems are equidistributed in phase space. By contrast, classical completely integrable systems generally have periodic orbits in phase space, and this is exhibited in a variety of ways in the high-energy limit of the eigenstates: typically, some form of concentration occurs in the semiclassical limit [math]\displaystyle{ \hbar \rightarrow 0 }[/math].

The model case of a Hamiltonian is the geodesic Hamiltonian on the cotangent bundle of a compact Riemannian manifold. The quantization of the geodesic flow is given by the fundamental solution of the Schrödinger equation

[math]\displaystyle{ U_t=\exp(it\sqrt{\Delta}) }[/math]

where [math]\displaystyle{ \sqrt{\Delta} }[/math] is the square root of the Laplace–Beltrami operator. The quantum ergodicity theorem of Shnirelman 1974, Zelditch, and Yves Colin de Verdière states that a compact Riemannian manifold whose unit tangent bundle is ergodic under the geodesic flow is also ergodic in the sense that the probability density associated to the nth eigenfunction of the Laplacian tends weakly to the uniform distribution on the unit cotangent bundle as n → ∞ in a subset of the natural numbers of natural density equal to one. Quantum ergodicity can be formulated as a non-commutative analogue of the classical ergodicity (T. Sunada).

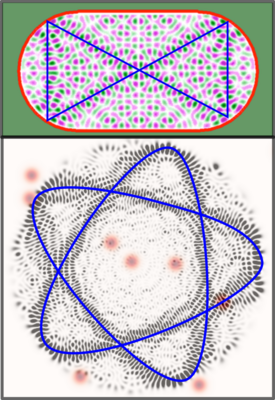
A scar in a stadium billiard (upper panel) and in a disordered quantum dot (lower panel) are example of nonergodic eigenstates allowed by the quantum ergodicity theorem. In both cases, the probability density of the eigenstates is concentrated along a periodic orbit of the classical counterpart (solid blue line). Although similar in appearance, the birth mechanism of the scars in the billiard and the quantum dot perturbed by potential bumps (red dots) are different: the former is explained the conventional scar theory,[1][2] whereas the latter is known as perturbation-induced scarring[3][4] (for further information, see Quantum scar).

Since a classically chaotic system is also ergodic, almost all of its trajectories eventually explore uniformly the entire accessible phase space. Thus, when translating the concept of ergodicity to the quantum realm, it is natural to assume that the eigenstates of the quantum chaotic system would fill the quantum phase space evenly (up to random fluctuations) in the semiclassical limit [math]\displaystyle{ \hbar \rightarrow 0 }[/math]. The quantum ergodicity theorems of Shnirelman, Zelditch, and Yves Colin de Verdière proves that the expectation value of an operator converges in the semiclassical limit to the corresponding microcanonical classical average. However, the quantum ergodicity theorem leaves open the possibility of eigenfunctions become sparse with serious holes as [math]\displaystyle{ \hbar \rightarrow 0 }[/math], leaving large but not macroscopic gaps on the energy manifolds in the phase space. In particular, the theorem allows the existence of a subset of macroscopically nonerdodic states which on the other hand must approach zero measure, i.e., the contribution of this set goes towards zero percent of all eigenstates when [math]\displaystyle{ \hbar \rightarrow 0 }[/math].[5]

For example, the theorem do not exclude quantum scarring, as the phase space volume of the scars also gradually vanishes in this limit.[1][5][6][2] A quantum eigenstate is scarred by periodic orbit if its probability density is on the classical invariant manifolds near and all along that periodic orbit is systematically enhanced above the classical, statistically expected density along that orbit.[5] In a simplified manner, a quantum scar refers to an eigenstate of whose probability density is enhanced in the neighborhood of a classical periodic orbit when the corresponding classical system is chaotic. In conventional scarring, the responsive periodic orbit is unstable.[1][5][6][2] The instability is a decisive point that separates quantum scars from a more trivial finding that the probability density is enhanced near stable periodic orbits due to the Bohr's correspondence principle. The latter can be viewed as a purely classical phenomenon, whereas in the former quantum interference is important. On the other hand, in the perturbation-induced quantum scarring,[3][7][8][9][4] some of the high-energy eigenstates of a locally perturbed quantum dot contain scars of short periodic orbits of the corresponding unperturbed system. Even though similar in appearance to ordinary quantum scars, these scars have a fundamentally different origin.,[3][7][4] In this type of scarring, there are no periodic orbits in the perturbed classical counterpart or they are too unstable to cause a scar in a conventional sense. Conventional and perturbation-induced scars are both a striking visual example of classical-quantum correspondence and of a quantum suppression of chaos (see the figure). In particular, scars are a significant correction to the assumption that the corresponding eigenstates of a classically chaotic Hamiltonian are only featureless and random. In some sense, scars can be considered as an eigenstate counterpart to the quantum ergodicity theorem of how short periodic orbits provide corrections to the universal random matrix theory eigenvalue statistics.

See also

External links

References

  1. ↑ 1.0 1.1 1.2 Heller, Eric J. (1984-10-15). "Bound-State Eigenfunctions of Classically Chaotic Hamiltonian Systems: Scars of Periodic Orbits". Physical Review Letters 53 (16): 1515–1518. doi:10.1103/PhysRevLett.53.1515. Bibcode: 1984PhRvL..53.1515H. https://link.aps.org/doi/10.1103/PhysRevLett.53.1515. 
  2. ↑ 2.0 2.1 2.2 Kaplan, L.; Heller, E. J. (1998-04-10). "Linear and Nonlinear Theory of Eigenfunction Scars" (in en). Annals of Physics 264 (2): 171–206. doi:10.1006/aphy.1997.5773. ISSN 0003-4916. Bibcode: 1998AnPhy.264..171K. https://www.sciencedirect.com/science/article/pii/S0003491697957730. 
  3. ↑ 3.0 3.1 3.2 Keski-Rahkonen, J.; Ruhanen, A.; Heller, E. J.; Räsänen, E. (2019-11-21). "Quantum Lissajous Scars". Physical Review Letters 123 (21): 214101. doi:10.1103/PhysRevLett.123.214101. PMID 31809168. Bibcode: 2019PhRvL.123u4101K. https://link.aps.org/doi/10.1103/PhysRevLett.123.214101. 
  4. ↑ 4.0 4.1 4.2 Keski-Rahkonen, Joonas (2020) (in en). Quantum Chaos in Disordered Two-Dimensional Nanostructures. Tampere University. ISBN 978-952-03-1699-0. https://trepo.tuni.fi/handle/10024/123296. 
  5. ↑ 5.0 5.1 5.2 5.3 Heller, Eric Johnson (2018). The semiclassical way to dynamics and spectroscopy. Princeton: Princeton University Press. ISBN 978-1-4008-9029-3. OCLC 1034625177. https://www.worldcat.org/oclc/1034625177. 
  6. ↑ 6.0 6.1 Kaplan, L (1999-01-01). "Scars in quantum chaotic wavefunctions" (in en). Nonlinearity 12 (2): R1–R40. doi:10.1088/0951-7715/12/2/009. ISSN 0951-7715. https://doi.org/10.1088/0951-7715/12/2/009. 
  7. ↑ 7.0 7.1 Luukko, Perttu J. J.; Drury, Byron; Klales, Anna; Kaplan, Lev; Heller, Eric J.; Räsänen, Esa (2016-11-28). "Strong quantum scarring by local impurities" (in en). Scientific Reports 6 (1): 37656. doi:10.1038/srep37656. ISSN 2045-2322. PMID 27892510. Bibcode: 2016NatSR...637656L. 
  8. ↑ Keski-Rahkonen, J.; Luukko, P. J. J.; Kaplan, L.; Heller, E. J.; Räsänen, E. (2017-09-20). "Controllable quantum scars in semiconductor quantum dots". Physical Review B 96 (9): 094204. doi:10.1103/PhysRevB.96.094204. Bibcode: 2017PhRvB..96i4204K. https://link.aps.org/doi/10.1103/PhysRevB.96.094204. 
  9. ↑ Keski-Rahkonen, J; Luukko, P J J; Åberg, S; Räsänen, E (2019-01-21). "Effects of scarring on quantum chaos in disordered quantum wells" (in en). Journal of Physics: Condensed Matter 31 (10): 105301. doi:10.1088/1361-648x/aaf9fb. ISSN 0953-8984. PMID 30566927. Bibcode: 2019JPCM...31j5301K. https://doi.org/10.1088/1361-648X/aaf9fb. 
  • Shnirelman, A I (1974), Ergodic properties of eigenfunctions, 29(6(180)), Uspekhi Mat. Nauk, Moscow, pp. 181–182 
  • Zelditch, S (2006), "Quantum ergodicity and mixing of eigenfunctions", in Françoise, Jean-Pierre; Naber, Gregory L.; Tsun, Tsou Sheung, Encyclopedia of mathematical physics. Vol. 1, 2, 3, 4, 5, Academic Press/Elsevier Science, Oxford, ISBN 9780125126601 
  • Sunada, T (1997), "Quantum ergodicity", Trend in Mathematics, Birkhauser Verlag, Basel, pp. 175–196 



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Quantum_ergodicity&oldid=2564921"