Ergodic hypothesis

Short description: Statistical mechanics hypothesis that all microstates are equiprobable for a given energy

The question of ergodicity in a perfectly collisionless ideal gas with specular reflections.

This device can trap fruit flies, but if it trapped atoms when placed in gas that already uniformly fills the available phase space, then both Liouville's theorem and the second law of thermodynamics would be violated.

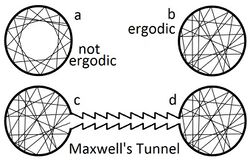
In physics and thermodynamics, the ergodic hypothesis says that, over long periods of time, the time spent by a system in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e., that all accessible microstates are equiprobable over a long period of time.

Liouville's theorem states that, for a Hamiltonian system, the local density of microstates following a particle path through phase space is constant as viewed by an observer moving with the ensemble (i.e., the convective time derivative is zero). Thus, if the microstates are uniformly distributed in phase space initially, they will remain so at all times. But Liouville's theorem does not imply that the ergodic hypothesis holds for all Hamiltonian systems.

The ergodic hypothesis is often assumed in the statistical analysis of computational physics. The analyst would assume that the average of a process parameter over time and the average over the statistical ensemble are the same. This assumption—that it is as good to simulate a system over a long time as it is to make many independent realizations of the same system—is not always correct. (See, for example, the Fermi–Pasta–Ulam–Tsingou experiment of 1953.)

Assumption of the ergodic hypothesis allows proof that certain types of perpetual motion machines of the second kind are impossible.

Systems that are ergodic are said to have the property of ergodicity; a broad range of systems in geometry, physics, and probability are ergodic. Ergodic systems are studied in ergodic theory.

Phenomenology

In macroscopic systems, the timescales over which a system can truly explore the entirety of its own phase space can be sufficiently large that the thermodynamic equilibrium state exhibits some form of ergodicity breaking. A common example is that of spontaneous magnetisation in ferromagnetic systems, whereby below the Curie temperature the system preferentially adopts a non-zero magnetisation even though the ergodic hypothesis would imply that no net magnetisation should exist by virtue of the system exploring all states whose time-averaged magnetisation should be zero. The fact that macroscopic systems often violate the literal form of the ergodic hypothesis is an example of spontaneous symmetry breaking.

However, complex disordered systems such as a spin glass show an even more complicated form of ergodicity breaking where the properties of the thermodynamic equilibrium state seen in practice are much more difficult to predict purely by symmetry arguments. Also conventional glasses (e.g. window glasses) violate ergodicity in a complicated manner. In practice this means that on sufficiently short time scales (e.g. those of parts of seconds, minutes, or a few hours) the systems may behave as solids, i.e. with a positive shear modulus, but on extremely long scales, e.g. over millennia or eons, as liquids, or with two or more time scales and plateaux in between.

Ergodic hypothesis in finance

Models used in finance and investment assume ergodicity, explicitly or implicitly. The ergodic hypothesis is prevalent in modern portfolio theory, discounted cash flow (DCF) models, and aggregate indicator models that infuse macroeconomics, among others.

The situations modeled by these theories can be useful. But often they are only useful during much, but not all, of any particular time period under study. They can therefore miss some of the largest deviations from the standard model, such as financial crises, debt crises and systemic risk in the banking system that occur only infrequently.

Nassim Nicholas Taleb has argued that a very important part of empirical reality in finance and investment is non-ergodic. An even statistical distribution of probabilities, where the system returns to every possible state an infinite number of times, is simply not the case we observe in situations where "absorbing states" are reached, a state where ruin is seen. The death of an individual, or total loss of everything, or the devolution or dismemberment of a nation state and the legal regime that accompanied it, are all absorbing states. Thus, in finance, path dependence matters. A path where an individual, firm or country hits a "stop"—an absorbing barrier, "anything that prevents people with skin in the game from emerging from it, and to which the system will invariably tend. Let us call these situations ruin, as the entity cannot emerge from the condition. The central problem is that if there is a possibility of ruin, cost benefit analyses are no longer possible."—will be non-ergodic. All traditional models based on standard probabilistic statistics break down in these extreme situations.

Ergodic hypothesis in social science

In the social sciences, the ergodic hypothesis corresponds to the assumption that individuals are representative of groups, and vice-versa, that group averages can adequately characterize what might be seen in an individual. This appears to not be the case: group level data often gives a poor indication of individual level variation, as individual standard deviations (SDs) tend to be almost eight times larger than group level SDs of the same people. Subsequently a third of the individual observations falls outside a 99.9% confidence interval of group level data.

See also

• Ergodic process
• Ergodic theory, a branch of mathematics concerned with a more general formulation of ergodicity
• Ergodicity
• Loschmidt's paradox
• Poincaré recurrence theorem
• Lindy effect