Physics:Scanning quantum dot microscopy
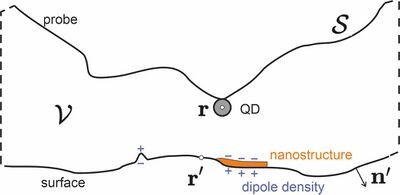
Scanning quantum dot microscopy (SQDM) is a scanning probe microscopy (SPM) that is used to image nanoscale electric potential distributions on surfaces.[1][2][3][4] The method quantifies surface potential variations via their influence on the potential of a quantum dot (QD) attached to the apex of the scanned probe. SQDM allows, for example, the quantification of surface dipoles originating from individual adatoms, molecules, or nanostructures. This gives insights into surface and interface mechanisms such as reconstruction or relaxation, mechanical distortion, charge transfer and chemical interaction. Measuring electric potential distributions is also relevant for characterizing organic and inorganic semiconductor devices which feature electric dipole layers at the relevant interfaces. The probe to surface distance in SQDM ranges from 2 nm[1][3] to 10 nm[2] and therefore allows imaging on non-planar surfaces or, e.g., of biomolecules with a distinct 3D structure. Related imaging techniques are Kelvin Probe Force Microscopy (KPFM) and Electrostatic Force Microscopy (EFM).
Working principle
In SQDM, the relation between the potential at the QD and the surface potential (the quantity of interest) is described by a boundary value problem of electrostatics. The boundary is given by the surfaces of sample and probe assumed to be connected at infinity. Then, the potential of a point-like QD at can be expressed using the Green's function formalism as a sum over volume and surface integrals,[5] where denotes the volume enclosed by and is the surface normal.
In this expression, depends on the charge density inside and on the potential on weighted by the Green's function
where satisfies the Laplace equation.
By specifying and thus defining the boundary conditions, these equations can be used to obtain the relation between and the surface potential for more specific measurement situations. The combination of a conductive probe and a conductive surface, a situation characterized by Dirichlet boundary conditions, has been described in detail.[4]
Conceptually, the relation between and links data in the imaging plane, obtained by reading out the QD potential, to data in the object surface - the surface potential. If the sample surface is approximated as locally flat and the relation between and therefore translationally invariant, the recovery of the object surface information from the imaging plane information is a deconvolution with a point spread function defined by the boundary value problem. In the specific case of a conductive boundary, the mutual screening of surface potentials by tip and surface lead to an exponential drop-off of the point spread function.[4][6] This causes the exceptionally high lateral resolution of SQDM at large tip-surface separations compared to, for example, KPFM.[3]
Practical implementation
Two methods have been reported to obtain the imaging plane information, i.e., the variations in the QD potential as the probe is scanned over the surface. In the compensation technique, is held at a constant value . The influence of the laterally varying surface potentials on is actively compensated by continuously adjusting the global sample potential via an external bias voltage .[1][7] is chosen such that it matches a discrete transition of the QD charge state and the corresponding change in probe-sample force is used in non-contact atomic force microscopy[8][9] to verify a correct compensation.
In an alternative method, the vertical component of the electric field at the QD position is mapped by measuring the energy shift of a specific optical transition of the QD[2][10] which occurs due to the Stark effect. This method requires an additional optical setup in addition to the SPM setup.
The object plane image can be interpreted as a variation of the work function, the surface potential, or the surface dipole density. The equivalence of these quantities is given by the Helmholtz equation. Within the surface dipole density interpretation, surface dipoles of individual nanostructures can be obtained by integration over a sufficiently large surface area.
Topographic information from SQDM
In the compensation technique, the influence of the global sample potential on depends on the shape of the sample surface in a way that is defined by the corresponding boundary value problem. On a non-planar surface, changes in can therefore not uniquely be assigned to either a change in surface potential or in surface topography if only a single charge state transition is tracked. For example, a protrusion in the surface affects the QD potential since the gating by works more efficiently if the QD is placed above the protrusion. If two transitions are used in the compensation technique the contributions of surface topography and potential can be disentangled and both quantities can be obtained unambiguously. The topographic information obtained via the compensation technique is an effective dielectric topography of metallic nature which is defined by the geometric topography and the dielectric properties of the sample surface or of a nanostructure.
References
- ↑ 1.0 1.1 1.2 Wagner, Christian; Green, Matthew F. B.; Leinen, Philipp; Deilmann, Thorsten; Krüger, Peter; Rohlfing, Michael; Temirov, Ruslan; Tautz, F. Stefan (2015-07-06). "Scanning Quantum Dot Microscopy" (in en). Physical Review Letters 115 (2). doi:10.1103/PhysRevLett.115.026101. ISSN 0031-9007. PMID 26207484. Bibcode: 2015PhRvL.115b6101W.
- ↑ 2.0 2.1 2.2 Cadeddu, D.; Munsch, M.; Rossi, N.; Gérard, J.-M.; Claudon, J.; Warburton, R. J.; Poggio, M. (2017-09-29). "Electric-Field Sensing with a Scanning Fiber-Coupled Quantum Dot" (in en). Physical Review Applied 8 (3). doi:10.1103/PhysRevApplied.8.031002. ISSN 2331-7019. Bibcode: 2017PhRvP...8c1002C.
- ↑ 3.0 3.1 3.2 Wagner, Christian; Green, Matthew. F. B.; Maiworm, Michael; Leinen, Philipp; Esat, Taner; Ferri, Nicola; Friedrich, Niklas; Findeisen, Rolf et al. (August 2019). "Quantitative imaging of electric surface potentials with single-atom sensitivity" (in en). Nature Materials 18 (8): 853–859. doi:10.1038/s41563-019-0382-8. ISSN 1476-1122. PMID 31182779. Bibcode: 2019NatMa..18..853W.
- ↑ 4.0 4.1 4.2 Wagner, Christian; Tautz, F Stefan (2019-11-27). "The theory of scanning quantum dot microscopy". Journal of Physics: Condensed Matter 31 (47): 475901. doi:10.1088/1361-648X/ab2d09. ISSN 0953-8984. PMID 31242473. Bibcode: 2019JPCM...31U5901W.
- ↑ Jackson, John David (1999). Classical electrodynamics. New York: Wiley. ISBN 978-0-471-30932-1. https://archive.org/details/classicalelectro0000jack_e8g9.
- ↑ Pumplin, Jon (July 1969). "Application of Sommerfeld-Watson Transformation to an Electrostatics Problem" (in en). American Journal of Physics 37 (7): 737–739. doi:10.1119/1.1975793. ISSN 0002-9505. Bibcode: 1969AmJPh..37..737P.
- ↑ Maiworm, Michael; Wagner, Christian; Temirov, Ruslan; Tautz, F. Stefan; Findeisen, Rolf (June 2018). "Two-degree-of-freedom control combining machine learning and extremum seeking for fast scanning quantum dot microscopy". 2018 Annual American Control Conference (ACC). Milwaukee, WI, USA: IEEE. pp. 4360–4366. doi:10.23919/ACC.2018.8431022. ISBN 978-1-5386-5428-6.
- ↑ Woodside, M. T. (2002-05-10). "Scanned Probe Imaging of Single-Electron Charge States in Nanotube Quantum Dots". Science 296 (5570): 1098–1101. doi:10.1126/science.1069923. PMID 12004123. Bibcode: 2002Sci...296.1098W.
- ↑ Stomp, Romain; Miyahara, Yoichi; Schaer, Sacha; Sun, Qingfeng; Guo, Hong; Grutter, Peter; Studenikin, Sergei; Poole, Philip et al. (2005-02-08). "Detection of Single-Electron Charging in an Individual InAs Quantum Dot by Noncontact Atomic-Force Microscopy" (in en). Physical Review Letters 94 (5). doi:10.1103/PhysRevLett.94.056802. ISSN 0031-9007. PMID 15783674. Bibcode: 2005PhRvL..94e6802S.
- ↑ Lee, Joonhee; Tallarida, Nicholas; Chen, Xing; Jensen, Lasse; Apkarian, V. Ara (June 2018). "Microscopy with a single-molecule scanning electrometer" (in en). Science Advances 4 (6). doi:10.1126/sciadv.aat5472. ISSN 2375-2548. PMID 29963637. Bibcode: 2018SciA....4.5472L.
External links
- https://www.fz-juelich.de/pgi/pgi-3/EN/Groups/LTSTM/Research/SQDM.html
- https://poggiolab.unibas.ch/research/Scanning%20Quantum%20Dot%20Microscopy/
- http://momalab.org/index.php/?action=devices
 |
