Physics:Spin echo

From HandWiki
Short description: Response of spin to electromagnetic radiation
Animation of spin echo, showing the response of spins (red arrows) in the blue Bloch sphere to the green pulse sequence

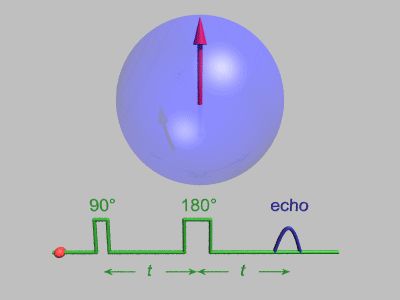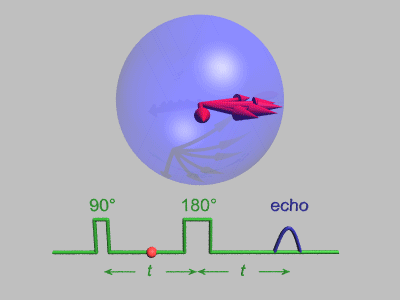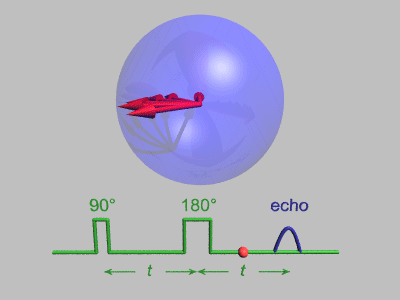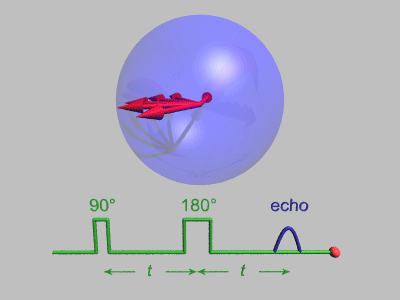
In magnetic resonance, a spin echo or Hahn echo is the refocusing of spin magnetisation by a pulse of resonant electromagnetic radiation.[1] Modern nuclear magnetic resonance (NMR) and magnetic resonance imaging (MRI) make use of this effect.

The NMR signal observed following an initial excitation pulse decays with time due to both spin relaxation and any inhomogeneous effects which cause spins in the sample to precess at different rates. The first of these, relaxation, leads to an irreversible loss of magnetisation. But the inhomogeneous dephasing can be removed by applying a 180° inversion pulse that inverts the magnetisation vectors.[2] Examples of inhomogeneous effects include a magnetic field gradient and a distribution of chemical shifts. If the inversion pulse is applied after a period t of dephasing, the inhomogeneous evolution will rephase to form an echo at time 2t. In simple cases, the intensity of the echo relative to the initial signal is given by e–2t/T2 where T2 is the time constant for spin–spin relaxation. The echo time (TE) is the time between the excitation pulse and the peak of the signal.[3]

Echo phenomena are important features of coherent spectroscopy which have been used in fields other than magnetic resonance including laser spectroscopy[4] and neutron scattering.

History

Echoes were first detected in nuclear magnetic resonance by Erwin Hahn in 1950,[5] and spin echoes are sometimes referred to as Hahn echoes. In nuclear magnetic resonance and magnetic resonance imaging, radiofrequency radiation is most commonly used.

In 1972 F. Mezei introduced spin-echo neutron scattering, a technique that can be used to study magnons and phonons in single crystals.[6] The technique is now applied in research facilities using triple axis spectrometers.

In 2020 two teams demonstrated [7][8] that when strongly coupling an ensemble of spins to a resonator, the Hahn pulse sequence does not just lead to a single echo, but rather to a whole train of periodic echoes. In this process the first Hahn echo acts back on the spins as a refocusing pulse, leading to self-stimulated secondary echoes.

Principle

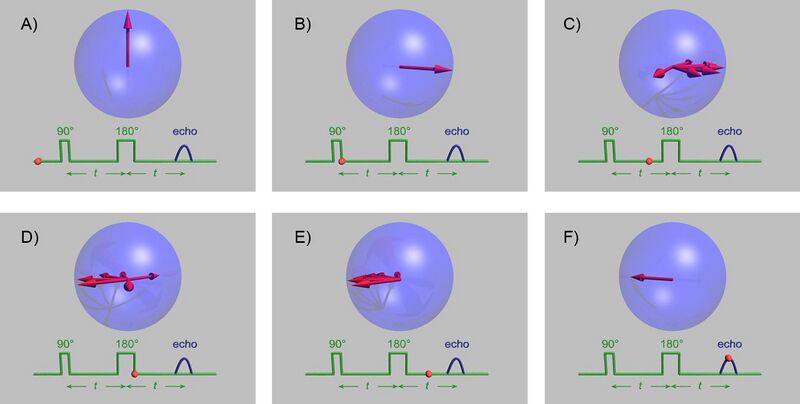
The spin-echo effect was discovered by Erwin Hahn when he applied two successive 90° pulses separated by short time period, but detected a signal, the echo, when no pulse was applied. This phenomenon of spin echo was explained by Erwin Hahn in his 1950 paper,[5] and further developed by Carr and Purcell who pointed out the advantages of using a 180° refocusing pulse for the second pulse.[9] The pulse sequence may be better understood by breaking it down into the following steps:

The spin-echo sequence
  1. The vertical red arrow is the average magnetic moment of a group of spins, such as protons. All are vertical in the vertical magnetic field and spinning on their long axis, but this illustration is in a rotating reference frame where the spins are stationary on average.
  2. A 90° pulse has been applied that flips the arrow into the horizontal (x–y) plane.
  3. Due to local magnetic field inhomogeneities (variations in the magnetic field at different parts of the sample that are constant in time), as the net moment precesses, some spins slow down due to lower local field strength (and so begin to progressively trail behind) while some speed up due to higher field strength and start getting ahead of the others. This makes the signal decay.
  1. A 180 degree pulse is now applied so that the slower spins lead ahead of the main moment and the fast ones trail behind.
  2. Progressively, the fast moments catch up with the main moment and the slow moments drift back toward the main moment. At some moment between E and F the sampling of the echo starts.
  3. Complete refocusing has occurred and at this time, an accurate T2 echo can be measured with all T2* effects removed. Quite separately, return of the red arrow towards the vertical (not shown) would reflect the T1 relaxation. 180 degrees is π radians so 180° pulses are often called π pulses.

Several simplifications are used in this sequence: no decoherence is included and each spin experiences perfect pulses during which the environment provides no spreading. Six spins are shown above and these are not given the chance to dephase significantly. The spin-echo technique is more useful when the spins have dephased more significantly such as in the animation below:

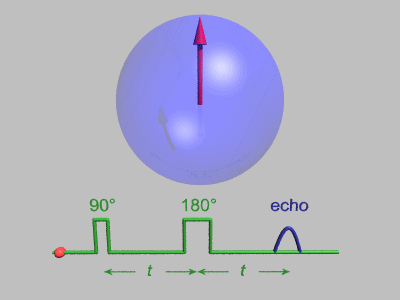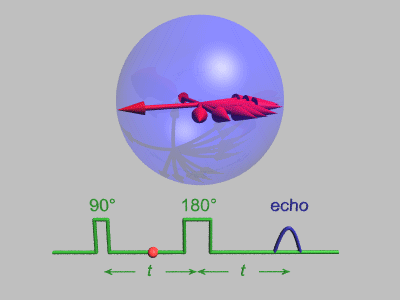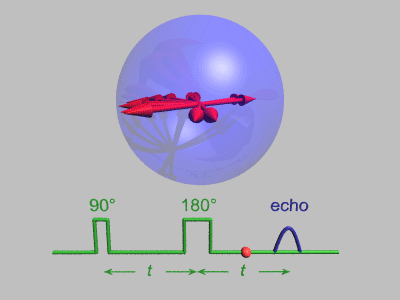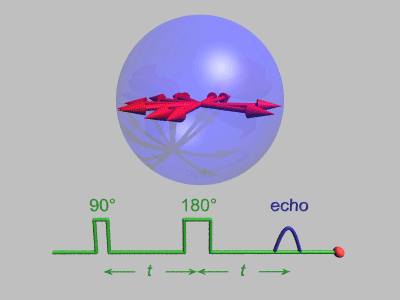
A spin echo with more spins and more dephasing

Spin-echo decay

A Hahn-echo decay experiment can be used to measure the spin–spin relaxation time, as shown in the animation below. The size of the echo is recorded for different spacings of the two pulses. This reveals the decoherence which is not refocused by the π pulse. In simple cases, an exponential decay is measured which is described by the T2 time.

Spin-echo decay

Stimulated echo

Hahn's 1950 paper[5] showed that another method for generating spin echoes is to apply three successive 90° pulses. After the first 90° pulse, the magnetization vector spreads out as described above, forming what can be thought of as a "pancake" in the x-y plane. The spreading continues for a time [math]\displaystyle{ \tau }[/math], and then a second 90° pulse is applied such that the "pancake" is now in the x-z plane. After a further time [math]\displaystyle{ T }[/math] a third pulse is applied and a stimulated echo is observed after waiting for a time [math]\displaystyle{ \tau }[/math] after the last pulse.

Photon echo

Hahn echos have also been observed at optical frequencies.[4] For this, resonant light is applied to a material with an inhomogeneously broadened absorption resonance. Instead of using two spin states in a magnetic field, photon echoes use two energy levels that are present in the material even in zero magnetic field.

Fast spin echo

Fast spin echo (RARE, FAISE or FSE[10][11][12]), also called turbo spin echo (TSE) is an MRI sequence that results in fast scan times. In this sequence, several 180 refocusing radio-frequency pulses are delivered during each echo time (TR) interval, and the phase-encoding gradient is briefly switched on between echoes.[13] The FSE/TSE pulse sequence superficially resembles a conventional spin-echo (CSE) sequence in that it uses a series of 180º-refocusing pulses after a single 90º-pulse to generate a train of echoes. The FSE/TSE technique, however, changes the phase-encoding gradient for each of these echoes (a conventional multi-echo sequence collects all echoes in a train with the same phase encoding). As a result of changing the phase-encoding gradient between echoes, multiple lines of k-space (i.e., phase-encoding steps) can be acquired within a given repetition time (TR). As multiple phase-encoding lines are acquired during each TR interval, FSE/TSE techniques may significantly reduce imaging time.[14]

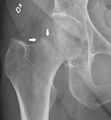
  • X-ray showing a suspected compressive subcapital fracture as a radiodense line

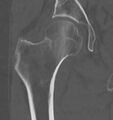
  • CT scan shows the same, atypical for a fracture since the cortex is coherent

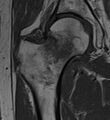
  • T1-weighted turbo spin echo MRI confirms a fracture, as the surrounding bone marrow has low signal from edema.

See also

References

  1. ↑ J. E. Tanner; E. O. Stejskal (2003). "Restricted Self-Diffusion of Protons in Colloidal Systems by the Pulsed-Gradient, Spin-Echo Method". The Journal of Chemical Physics 49 (4): 1768. doi:10.1063/1.1670306. Bibcode: 1968JChPh..49.1768T. 
  2. ↑ Malcolm H. Levitt; Ray Freeman (1979). "NMR population inversion using a composite pulse". Journal of Magnetic Resonance 33 (2): 473–476. doi:10.1016/0022-2364(79)90265-8. Bibcode: 1979JMagR..33..473L. 
  3. ↑ Dan J Bell and J Yeung. "Echo time". https://radiopaedia.org/articles/echo-time. Retrieved 2017-09-24. 
  4. ↑ 4.0 4.1 Kurnit, N. A.; Abella, I. D.; Hartmann, S. R. (1964). "Observation of a photon echo". Physical Review Letters 13 (19): 567–568. doi:10.1103/PhysRevLett.13.567. Bibcode: 1964PhRvL..13..567K. 
  5. ↑ 5.0 5.1 5.2 Hahn, E.L. (1950). "Spin echoes". Physical Review 80 (4): 580–594. doi:10.1103/PhysRev.80.580. Bibcode: 1950PhRv...80..580H. 
  6. ↑ Mezei, F. (1972), "Neutron spin echo: A new concept in polarized thermal neutron techniques", Zeitschrift für Physik, 255(2), pp. 146–160.
  7. ↑ Weichselbaumer, Stefan; Zens, Matthias; Zollitsch, Christoph W.; Brandt, Martin S.; Rotter, Stefan; Gross, Rudolf; Huebl, Hans (2020). "Echo Trains in Pulsed Electron Spin Resonance of a Strongly Coupled Spin Ensemble". Physical Review Letters 125 (13): 137701. doi:10.1103/PhysRevLett.125.137701. PMID 33034465. Bibcode: 2020PhRvL.125m7701W. https://discovery.ucl.ac.uk/id/eprint/10111782/. 
  8. ↑ Debnath, Kamanasish; Dold, David; Morton, John J. L.; Mølmer, Klaus (2020). "Self-Stimulated Pulse Echo Trains from Inhomogeneously Broadened Spin Ensembles". Physical Review Letters 125 (13): 137702. doi:10.1103/PhysRevLett.125.137702. PMID 33034472. Bibcode: 2020PhRvL.125m7702D. 
  9. ↑ Carr, H. Y.; Purcell, E. M. (1954). "Effects of Diffusion on Free Precession in Nuclear Magnetic Resonance Experiments". Physical Review 94 (3): 630–638. doi:10.1103/PhysRev.94.630. Bibcode: 1954PhRv...94..630C. 
  10. ↑ Melki, Philippe S.; Mulkern, Robert V.; Panych, Lawrence P.; Jolesz, Ferenc A. (May–June 1991). "Comparing the FAISE method with conventional dual-echo sequences" (in en). Journal of Magnetic Resonance Imaging 1 (3): 319–326. doi:10.1002/jmri.1880010310. PMID 1802145. https://onlinelibrary.wiley.com/doi/10.1002/jmri.1880010310. 
  11. ↑ Melki, Philippe S.; Jolesz, Ferenc A.; Mulkern, Robert V. (August 1992). "Partial RF echo planar imaging with the FAISE method. I. Experimental and theoretical assessment of artifact" (in en). Magnetic Resonance in Medicine 26 (2): 328–341. doi:10.1002/mrm.1910260212. PMID 1513254. https://onlinelibrary.wiley.com/doi/10.1002/mrm.1910260212. 
  12. ↑ Melki, Philippe S.; Jolesz, Ferenc A.; Mulkern, Robert V. (August 1992). "Partial RF echo-planar imaging with the FAISE method. II. Contrast equivalence with spin-echo sequences" (in en). Magnetic Resonance in Medicine 26 (2): 342–354. doi:10.1002/mrm.1910260213. PMID 1513255. https://onlinelibrary.wiley.com/doi/10.1002/mrm.1910260213. 
  13. ↑ "Chapter 8: Fast Pulse sequences". How does MRI work?: An Introduction to the Physics and Function of Magnetic Resonance Imaging (2nd ed.). Springer Science & Business Media. 2008. p. 64. ISBN 978-3-540-37845-7. https://books.google.com/books?id=wbizuPJjD04C&pg=PT64. 
  14. ↑ "What is Fast (Turbo) Spin Echo imaging?". http://mriquestions.com/what-is-fsetse.html. 

Further reading

  • Ray Freeman (1999). Spin Choreography: Basic Steps in High Resolution NMR. Oxford University Press. ISBN 978-0-19-850481-8. 
  • Arthur Schweiger; Gunnar Jeschke (2001). Principles of Pulse Electron Paramagnetic Resonance. Oxford University Press. ISBN 978-0-19-850634-8. 

External links

Animations and simulations



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Spin_echo&oldid=3281081"