Physics:Tokamak sawtooth

Short description: Relaxation in the core of tokamak plasmas

The safety factor profile shortly before and shortly after a sawtooth relaxation in a numerical resistive MHD simulation. After the relaxation, [math]\displaystyle{ q \gt 1 }[/math] and the q profile has a broader, more square-like shape.

Magnetic reconnection during a numerical resistive MHD simulation of a sawtooth relaxation. The arrows showing the direction of the flow are overlaid on top of a plot of the toroidal current density. The size of the arrows corresponds to the magnitude of the flow velocity.

A sawtooth is a relaxation that is commonly observed in the core of tokamak plasmas, first reported in 1974. The relaxations occur quasi-periodically and cause a sudden drop in the temperature and density in the center of the plasma. A soft-xray pinhole camera pointed toward the plasma core during sawtooth activity will produce a sawtooth-like signal. Sawteeth effectively limit the amplitude of the central current density. The Kadomtsev model of sawteeth is a classic example of magnetic reconnection. Other repeated relaxation oscillations occurring in tokamaks include the edge localized mode (ELM) which effectively limits the pressure gradient at the plasma edge and the fishbone instability which effectively limits the density and pressure of fast particles.

Kadomtsev model

An often cited description of the sawtooth relaxation is that by Kadomtsev. The Kadomtsev model uses a resistive magnetohydrodynamic (MHD) description of the plasma. If the amplitude of the current density in the plasma core is high enough so that the central safety factor [math]\displaystyle{ q_{0} }[/math] is below unity, a [math]\displaystyle{ m=1 }[/math] linear eigenmode will be unstable, where [math]\displaystyle{ m }[/math] is the poloidal mode number. This instability may be the internal kink mode, resistive internal kink mode or [math]\displaystyle{ m=1 }[/math] tearing mode. The eigenfunction of each of these instabilities is a rigid displacement of the region inside [math]\displaystyle{ q=1 }[/math]. The mode amplitude will grow exponentially until it saturates, significantly distorting the equilibrium fields, and enters the nonlinear phase of evolution. In the nonlinear evolution, the plasma core inside the [math]\displaystyle{ q=1 }[/math] surface is driven into a resistive reconnection layer. As the flux in the core is reconnected, an island grows on the side of the core opposite the reconnection layer. The island replaces the core when the core has completely reconnected so that the final state has closed nested flux surfaces, and the center of the island is the new magnetic axis. In the final state, the safety factor is greater than unity everywhere. The process flattens temperature and density profiles in the core.

After a relaxation, the flattened temperature and safety factor profiles become peaked again as the core reheats on the energy confinement time scale, and the central safety factor drops below unity again as the current density resistively diffuses back into the core. In this way, the sawtooth relaxation occurs repeatedly with average period [math]\displaystyle{ \tau_{saw} }[/math].

The Kadomtsev picture of sawtoothing in a resistive MHD model was very successful at describing many properties of the sawtooth in early tokamak experiments. However as measurements became more accurate and tokamak plasmas got hotter, discrepancies appeared. One discrepancy is that relaxations caused a much more rapid drop in the central plasma temperature of hot tokamaks than predicted by the resistive reconnection in the Kadomtsev model. Some insight into fast sawtooth crashes was provided by numerical simulations using more sophisticated model equations and by the Wesson model. Another discrepancy found was that the central safety factor was observed to be significantly less than unity immediately after some sawtooth crashes. Two notable explanations for this are incomplete reconnection and rapid rearrangement of flux immediately after a relaxation.

Wesson model

The Wesson model offers an explanation fast sawtooth crashes in hot tokamaks. Wesson's model describes a sawtooth relaxation based on the non-linear evolution of the quasi-interchange (QI) mode. The nonlinear evolution of the QI does not involve much reconnection, so it does not have Sweet-Parker scaling and the crash can proceed much faster in high temperature, low resistivity plasmas given a resistive MHD model. However more accurate experimental methods for measuring [math]\displaystyle{ q }[/math] profiles in tokamaks were developed later. It was found that the profiles during sawtoothing discharges are not necessarily flat with [math]\displaystyle{ q\approx1 }[/math] as needed by Wesson's description of the sawtooth. Nevertheless, Wesson-like relaxations have been observed experimentally on occasion.

Numerical simulation

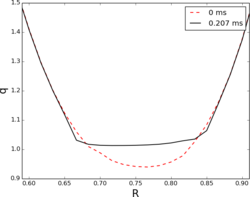
The first results of a numerical simulation that provided verification of the Kadomtsev model were published in 1976. This simulation demonstrated a single Kadomtsev-like sawtooth relaxation. In 1987 the first results of a simulation demonstrating repeated, quasi-periodic sawtooth relaxations was published. Results from resistive MHD simulations of repeated sawtoothing generally give reasonably accurate crash times and sawtooth period times for smaller tokamaks with relatively small Lundquist numbers.

In large tokamaks with larger Lundquist numbers, sawtooth relaxations are observed to occur much faster than predicted by the resistive Kadomtsev model. Simulations using two-fluid model equations or non-ideal terms in Ohm's law besides the resistive term, such as the Hall and electron inertia terms, can account for the fast crash times observed in hot tokamaks. These models can allow much faster reconnection at low resistivity.

Giant sawteeth

Large, hot tokamaks with significant populations of fast particles sometimes see so called "giant sawteeth". Giant sawteeth are much larger relaxations and may cause disruptions. They are a concern for ITER. In hot tokamaks, under some circumstances, minority hot particle species can stabilize the sawtooth instability. [math]\displaystyle{ q_{0} }[/math] drops well below unity during the long period of stabilization, until instability is triggered, and the resulting crash is very large.