Physics:Tonti diagram

The Tonti diagram, created by the Italian physicist and mathematician Enzo Tonti, is a diagram that classifies variables and equations of physical theories of classical and relativistic physics. The theories involved are: particle dynamics, analytical mechanics, mechanics of deformable solids, fluid mechanics, electromagnetism, gravitation, heat conduction, and irreversible thermodynamics. The classification stems from the observation that each physical variable has a well-defined association with a space and a time element, as shown in Fig. 1, which can be grasped from the corresponding global variable and from its measuring process.

Historical note

The starting point of this classification stems from a remark by Maxwell. Speaking about analogies in different physical theories, Maxwell wrote in 1871:

Of the factors which compose it [energy], one is referred to unit of length, and the other to unit of area. This gives what I regard as a very important distinction among vector quantities.

This remark leads us to a distinction between vectors referred to lines and vectors referred to surfaces. This is not customarily considered in vector calculus or in physics. In electromagnetism, hence, vectors E and H are associated with lines, and vectors D and B are associated with surfaces. This distinction leads to a classification of physical variables based on their association with space elements. Maxwell continues:

It is only through the progress of science in recent times that we have become acquainted with so large a number of physical quantities that a classification of them is desirable. [...] But the classification which I now refer to is founded on the mathematical or formal analogy of the different quantities, and not on the matter to which they belong.

The classification diagram arises from an analysis of the association of physical variables in different physical theories, whatever their mathematical nature, i.e. scalars, vectors, tensors, etc., with space and time elements.

The three kinds of physical quantities

Physics, compared to other natural sciences, has the great privilege of considering the quantitative attributes of physical systems and from these originate the physical quantities, which can be scalars, vectors, tensors, etc. Physical quantities can be divided into three main categories: physical variables, physical parameters and fundamental constants.

Global variables in space and field variables

The term space-global variables refers to all physical variables that are not densities of other variables. Distinguishing between global variables and corresponding densities is essential. Mass density is given by the ratio of mass to volume, mass being the global variable. Pressure is the ratio of the normal force on an element of plane surface to the surface area, therefore the normal force is the global variable and the pressure is its surface density. The strain of a bar is the ratio of the elongation to its original length, elongation being the global variable and strain the line density. The very fact that we create volume, surface or line densities highlights that the corresponding global variables are associated with volumes, surfaces and lines. Every density is obtained by dividing a global variable by the extension of the associated space element. The mathematical treatment of physics also customarily considers the limit of this ratio to obtain a pointwise density, i.e. a field variable. Generally, field variables are preferred to global variables, to the extent that we express the global variables as integrals of the respective field variables, and call them integral variables. Integral variables are global variables, but there are also global variables which are associated with points, and which, therefore, cannot be considered integral variables. Hence, global variables form a broader class compared to integral variables; for which reason, in view of the classification, the use of the term “global variables” is preferred to that of "integral variables".

Global variables in time and rates

The term time-global variables is used to indicate variables that are not rates of other variables. Displacement, impulse, momentum and position vector are therefore global variables. Displacement and impulse are associated with time intervals, while momentum and position vector are associated with instants. This is evident if we think that we can perform the rates of the first two variables obtaining velocity and force respectively, while we cannot perform the rates of the last two variables.

The three kinds of physical variables

The physical variables, both global variables and densities, in turn, can be divided into three classes: those characterising the configuration of a system or a field, those describing the source of a phenomenon or a field, and finally energy variables. Every physical system, even a field, has its own “configuration”, and the variables describing this configuration are called configuration variables. Each field has its sources (for example, electric charges are the source of electric fields, heat generators are the source of thermal fields and forces are the source of motion and deformation): variables describing sources are called source variables. The third category, that of energy variables, is created by multiplying a configuration variable by a source variable. The fundamental problem of a field is finding the configuration of the field at every time instant, given the spatial distribution and the intensity of its sources (which is to say: given the causes, determine the effects).

Space and time elements

By the term "space elements" we intend points, lines, surfaces and volumes, which are denoted P,L,S and V respectively. By the term "time elements" we intend time instants and time intervals, which are denoted I and T respectively. Space elements are naturally classified according to their dimension, from the smallest to the biggest, i.e. points, lines, surfaces and volumes. The same classification applies to time elements, i.e. instants and intervals.

Association with space elements

Figure 1.The figure shows a number of physical variables with the space and time elements they are associated with.

Figure 2. Every space element can be endowed with one of the two possible orientations: inner and outer.

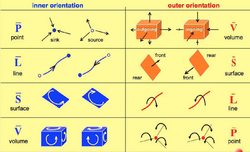
All fluxes (e.g. magnetic flux, electric flux, vortex flux) make reference to a surface (S), all variables expressed by a line integral (e.g. electromotive force, velocity circulation, magnetomotive force) make reference to a line (L) and all contents (e.g. of energy, mass, entropy, etc.) make reference to a volume (V). Lastly all potentials (e.g. electric potential, velocity potential, temperature) make reference to a point (P).

Association with time elements

A similar association exists between time-global variables and time elements. Therefore, a displacement is associated with a time interval (T), whereas a position vector is associated with a time instant (I). In this association the measuring process must be taken into account, because temperature is referred to an instant but its measurement involves a time interval - the one needed to reach thermal equilibrium. Therefore, the temperature is said to be associated with a time interval (T). Similarly, the measurement of a force requires a mechanical equilibrium to be reached, hence it is associated with a time interval (T).

Figure 3. Left) A two-dimensional cell complex and its dual; right) the classification of its space elements.

Inherited association of field variables

Since in each field of physics the global variables are associated with a space and a time element, the association of the corresponding densities and the rates with the space and time element of the corresponding global variable is spontaneous. The densities and the rates are said to inherit the association from their corresponding global variables. The same inherited association remains once we have performed the limit to obtain the field variables.

Orientation of space elements

In this classification, the orientation of the space elements has a fundamental role. There are two kinds of orientation: inner and outer orientation, as shown in Fig. 2.

There is a surprising correspondence between the role that a physical variable plays in a theory and the type of orientation of the corresponding space element: a detailed analysis of physical variables shows that the configuration variables are associated with the space elements endowed with inner orientation while the source and the energy variables are associated with the outer orientation.

Figure 4. Left) A three-dimensional cell complex and its dual; right) the classification of its space elements.

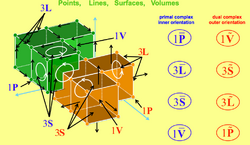
Cell complexes

To highlight the four space elements, it is expedient to divide a region of space into many cells, thus creating a cell complex. The vertices represent points, the edges lines, the faces surfaces and the cells themselves volumes. Each of these elements can be given an inner orientation. Since we also need space elements with outer orientation, it is expedient to consider the dual complex, obtained by joining the centroids of the cells belonging to the primal complex. Doing so, we see that the inner orientation of each element of the primal complex induces an outer orientation on the corresponding element of the dual complex.

Figures 3 and 4 show how the space elements of the primal complex, which are endowed with inner orientation, induce an outer orientation on the elements of the dual complex. Moreover, the space elements of the two complexes can be arranged in a diagram such as the one shown on the right-hand side of the figures.

A cell complex and its dual constitute a valid framework to describe the association of physical variables with the oriented space elements. To be precise, the configuration variables, which are associated with space elements with inner orientation, may be associated with the elements of the primal complex, while the source variables, which are associated with the space elements with an outer orientation, can be associated with the elements of the dual complex.

Orientation of time elements

Figure 5. Time elements. I_k = time instants; T_k = time intervals; r_k = position vector; u_k = displacement.

At first glance, the notions of inner and outer orientation of a time element may appear strange, certainly unusual. Consider a subdivision of the time axis into many adjacent time intervals. Doing so, we have constructed a one-dimensional cell complex in time. Considering now the middle instants of each time interval we have a second cell complex in time. The first complex is called primal and the second dual.

Primal complex, inner orientation: the fact that the time axis is oriented implies that each time interval is oriented: this is the inner orientation of the primal time intervals. Since the variation of a time function φ (t) is defined as Δφ = + φ (t + h)-φ (t), in order to conceive the "+" and "-" signs of this formula as incidence numbers between a time interval and its bounding instants, these should be considered as "sinks".

Dual complex, outer orientation: the middle instant of each time interval is called dual time instant and we can give it the same orientation of the primal time interval. This is called outer orientation of the dual time instant. In turn, the time intervals connecting two adjacent dual time instants are called dual time intervals. Once more we can assign them the orientation induced by the primal time instants, as shown in Fig. 5. This is called outer orientation of the dual time intervals.

The birth of the classification diagram

Figure 6. Classification diagram for electrostatics.

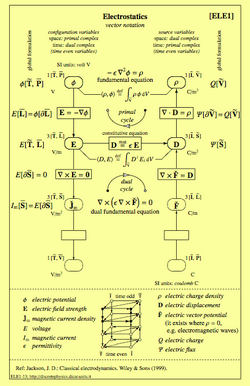
The fact that physical variables are associated with space and time elements endowed with inner or outer orientation and that space and time elements of a primal and a dual cell complex can be classified as shown on the right-hand side of Figs. 3 and 4, suggests a corresponding classification of physical variables. Consider, as an example, the classification diagram of electrostatics, shown in Fig. 6. The left column includes those physical variables associated with the primal cell complex, whose elements are endowed with inner orientation: these are the configuration variables. The right column includes those physical variables associated with the dual cell complex, whose elements are endowed with outer orientation: these are the source variables.

The equations linking the variables are contained in the rectangular boxes. The equations in each vertical column are balance equations, circuital equations and gradient-forming equations. They have a topological structure and are called topological equations. Those that link configuration variables to source variables—contained in the horizontal links—are material or constitutive equations, and belong to the category of phenomenological equations.

The time diagram

Figure 7. Classification diagram for particle dynamics.

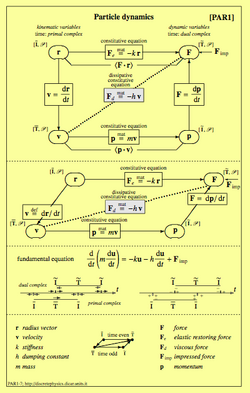
Particle dynamics, analytical mechanics and electric networks make use of space-global variables that depend only on the time variable. Referring here to particle dynamics, we see that configuration variables are geometrical and kinematic variables, while source variables are static and dynamic variables. In Fig. 7 we see that kinematic variables lie in the left column while dynamic variables lie in the right one. The diagram shows three phenomenological equations: those connecting two variables on the same level describe a reversible relation (i.e. a non-dissipative relation), while those linking force with velocity describe an irreversible relation (i.e. a dissipative relation). The dissipative nature is shown by the fact that one variable, velocity, changes sign under reversal of motion, while the other, force, does not.

The space-time diagram

Figure 8. The two classification diagrams of space-time elements.

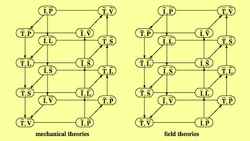
Since every global physical variable is associated with both a time and a space element, it appears useful to have a classification diagram combining space and time elements. When the four space elements P, L, S and V are coupled with the two time elements I and T we obtain eight possible combinations. Furthermore, if one considers that each space element and each time element can be endowed with two orientations, inner and outer, we must combine the 4x2 oriented space elements with the 2x2 oriented time elements, thus obtaining 32 possible space-time combinations. Fig. 8 shows the two possible classification diagrams of the space-time elements. The first version associates the space elements endowed with inner orientation with the time elements endowed with inner orientation and vice versa: it is the case of mechanics in all its manifestations, such as particle and analytical mechanics, mechanics of deformable solids and fluid mechanics. The second version associates the space elements endowed with inner orientation with the time elements endowed with outer orientation and vice versa. It is the case of field theories such as electromagnetism, gravitation, thermal conduction and irreversible thermodynamics.

The space-time diagrams show clearly which phenomenological equations describe irreversible phenomena: they are the ones that link variables that are on the same level but connect a box on the front-left side with a box on the back-right side.

See also

• Heat transfer
• Electromagnetism
• Solid mechanics
• Fluid dynamics

External links

• Discrete Physics
• Metodo delle celle
• Chronological Tables of famous people
• Research gate