Poincaré–Miranda theorem

Short description: Generalisation of the intermediate value theorem

In mathematics, the Poincaré–Miranda theorem is a generalization of intermediate value theorem, from a single function in a single dimension, to n functions in n dimensions. It says as follows:

Consider [math]\displaystyle{ n }[/math] continuous, real-valued functions of [math]\displaystyle{ n }[/math] variables, [math]\displaystyle{ f_1,\ldots, f_n:[-1,1]^n\to \mathbb R }[/math]. Assume that for each variable [math]\displaystyle{ x_i }[/math], the function [math]\displaystyle{ f_i }[/math] is nonpositive when [math]\displaystyle{ x_i=-1 }[/math] and nonnegative when [math]\displaystyle{ x_i=1 }[/math]. Then there is a point in the [math]\displaystyle{ n }[/math]-dimensional cube [math]\displaystyle{ [-1,1]^n }[/math] in which all functions are simultaneously equal to [math]\displaystyle{ 0 }[/math].

The theorem is named after Henri Poincaré - who conjectured it in 1883 - and Carlo Miranda - who in 1940 showed that it is equivalent to the Brouwer fixed-point theorem. It is sometimes called the Miranda theorem or the Bolzano-Poincare-Miranda theorem.

Intuitive description

A graphical representation of Poincaré–Miranda theorem for n = 2

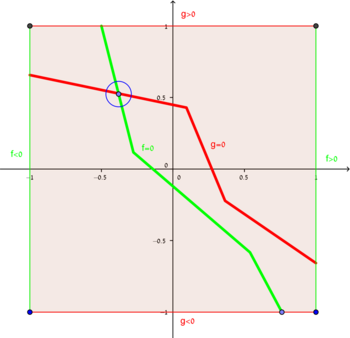
The picture on the right shows an illustration of the Poincaré–Miranda theorem for n = 2 functions. Consider a couple of functions (f,g) whose domain of definition is [-1,1]² (i.e., the unit square). The function f is negative on the left boundary and positive on the right boundary (green sides of the square), while the function g is negative on the lower boundary and positive on the upper boundary (red sides of the square). When we go from left to right along any path, we must go through a point in which f is 0. Therefore, there must be a "wall" separating the left from the right, along which f is 0 (green curve inside the square). Similarly, there must be a "wall" separating the top from the bottom, along which g is 0 (red curve inside the square). These walls must intersect in a point in which both functions are 0 (blue point inside the square).

Generalizations

The simplest generalization, as a matter of fact a corollary, of this theorem is the following one. For every variable x_i, let a_i be any value in the range [sup_xi = 0 f_i, inf_xi = 1 f_i]. Then there is a point in the unit cube in which for all i:

[math]\displaystyle{ f_i=a_i }[/math].

This statement can be reduced to the original one by a simple translation of axes,

[math]\displaystyle{ x^\prime_i=x_i\qquad y^\prime_i=y_i-a_i\qquad \forall i\in\{1,\dots,n\} }[/math]

where

• x_i are the coordinates in the domain of the function
• y_i are the coordinates in the codomain of the function.

By using topological degree theory it is possible to prove yet another generalization. Poincare-Miranda was also generalized to infinite-dimensional spaces.

See also

• The Steinhaus chessboard theorem is a discrete theorem that can be used to prove the Poincare-Miranda theorem.

Further reading

• Alefeld, Götz; Frommer, Andreas; Heindl, Gerhard; Mayer, Jan (2004). "On the existence theorems of Kantorovich, Miranda and Borsuk." (in en). ETNA. Electronic Transactions on Numerical Analysis [electronic only] 18: 102–111. http://dml.mathdoc.fr/item/02156105/.