Prime reciprocal magic square

Short description: Type of magic square

A prime reciprocal magic square is a magic square using the decimal digits of the reciprocal of a prime number.

Formulation

Basics

In decimal, unit fractions [math]\displaystyle{ \tfrac {1}{2} }[/math] and [math]\displaystyle{ \tfrac {1}{5} }[/math] have no repeating decimal, while [math]\displaystyle{ \tfrac {1}{3} }[/math] repeats [math]\displaystyle{ 0.3333\dots }[/math] indefinitely. The remainder of [math]\displaystyle{ \tfrac {1}{7} }[/math], on the other hand, repeats over six digits as, [math]\displaystyle{ 0.\bold{1}42857\bold{1}42857\bold{1}\dots }[/math]

Consequently, multiples of one-seventh exhibit cyclic permutations of these six digits:

[math]\displaystyle{ \begin{align} 1/7 & = 0.1 4 2 8 5 7\dots \\ 2/7 & = 0.2 8 5 7 1 4\dots \\ 3/7 & = 0.4 2 8 5 7 1\dots \\ 4/7 & = 0.5 7 1 4 2 8\dots \\ 5/7 & = 0.7 1 4 2 8 5\dots \\ 6/7 & = 0.8 5 7 1 4 2\dots \end{align} }[/math]

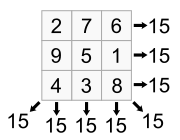
If the digits are laid out as a square, each row and column sums to [math]\displaystyle{ 1 + 4 + 2 + 8 + 5 + 7 = 27. }[/math] This yields the smallest base-10 non-normal, prime reciprocal magic square

[math]\displaystyle{ 1 }[/math]	[math]\displaystyle{ 4 }[/math]	[math]\displaystyle{ 2 }[/math]	[math]\displaystyle{ 8 }[/math]	[math]\displaystyle{ 5 }[/math]	[math]\displaystyle{ 7 }[/math]
[math]\displaystyle{ 2 }[/math]	[math]\displaystyle{ 8 }[/math]	[math]\displaystyle{ 5 }[/math]	[math]\displaystyle{ 7 }[/math]	[math]\displaystyle{ 1 }[/math]	[math]\displaystyle{ 4 }[/math]
[math]\displaystyle{ 4 }[/math]	[math]\displaystyle{ 2 }[/math]	[math]\displaystyle{ 8 }[/math]	[math]\displaystyle{ 5 }[/math]	[math]\displaystyle{ 7 }[/math]	[math]\displaystyle{ 1 }[/math]
[math]\displaystyle{ 5 }[/math]	[math]\displaystyle{ 7 }[/math]	[math]\displaystyle{ 1 }[/math]	[math]\displaystyle{ 4 }[/math]	[math]\displaystyle{ 2 }[/math]	[math]\displaystyle{ 8 }[/math]
[math]\displaystyle{ 7 }[/math]	[math]\displaystyle{ 1 }[/math]	[math]\displaystyle{ 4 }[/math]	[math]\displaystyle{ 2 }[/math]	[math]\displaystyle{ 8 }[/math]	[math]\displaystyle{ 5 }[/math]
[math]\displaystyle{ 8 }[/math]	[math]\displaystyle{ 5 }[/math]	[math]\displaystyle{ 7 }[/math]	[math]\displaystyle{ 1 }[/math]	[math]\displaystyle{ 4 }[/math]	[math]\displaystyle{ 2 }[/math]

In contrast with its rows and columns, the diagonals of this square do not sum to 27; however, their mean is 27, as one diagonal adds to 23 while the other adds to 31.

All prime reciprocals in any base with a [math]\displaystyle{ p - 1 }[/math] period will generate magic squares where all rows and columns produce a magic constant, and only a select few will be full, such that their diagonals, rows and columns collectively yield equal sums.

Decimal expansions

In a full, or otherwise prime reciprocal magic square with [math]\displaystyle{ p - 1 }[/math] period, the even number of [math]\displaystyle{ k }[/math]−th rows in the square are arranged by multiples of [math]\displaystyle{ 1/p }[/math] — not necessarily successively — where a magic constant can be obtained.

For instance, an even repeating cycle from an odd, prime reciprocal of [math]\displaystyle{ p }[/math] that is divided into [math]\displaystyle{ n }[/math]−digit strings creates pairs of complementary sequences of digits that yield strings of nines (9) when added together:

[math]\displaystyle{ \begin{align} 1/7 = & \text { } 0.142\;857\dots \\ + & \text { } 0.857\;142\ldots = 6/7\\ & ------------ \\ & \text { } 0.999\;999\ldots \\ \\ 1/13 = & \text { } 0.076\;923\;076\;923\dots \\ + & \text { } 0.923\;076\;923\;076\ldots = 12/13\\ & ------------ \\ & \text { } 0.999\;999\;999\;999\ldots \\ \\ 1/19 = & \text { } 0.052631578\;947368421\dots \\ + & \text { } 0.947368421\;052631578\ldots = 18/19\\ & ------------ \\ & \text { } 0.999999999\;999999999\dots \\ \end{align} }[/math]

This is a result of Midy's theorem. These complementary sequences are generated between multiples of prime reciprocals that add to 1.

More specifically, a factor [math]\displaystyle{ n }[/math] in the numerator of the reciprocal of a prime number [math]\displaystyle{ p }[/math] will shift the decimal places of its decimal expansion accordingly,

[math]\displaystyle{ \begin{align} 1/23 & = 0.04347826\;08695652\;173913\ldots \\ 2/23 & = 0.08695652\;17391304\;347826\ldots \\ 4/23 & = 0.17391304\;34782608\;695652\ldots \\ 8/23 & = 0.34782608\;69565217\;391304\ldots \\ 16/23 & = 0.69565217\;39130434\;782608\ldots \\ \end{align} }[/math]

In this case, a factor of 2 moves the repeating decimal of [math]\displaystyle{ \tfrac {1}{23} }[/math] by eight places.

A uniform solution of a prime reciprocal magic square, whether full or not, will hold rows with successive multiples of [math]\displaystyle{ 1/p }[/math]. Other magic squares can be constructed whose rows do not represent consecutive multiples of [math]\displaystyle{ 1/p }[/math], which nonetheless generate a magic sum.

Magic constant

Magic squares based on reciprocals of primes [math]\displaystyle{ p }[/math] in bases [math]\displaystyle{ b }[/math] with periods [math]\displaystyle{ p - 1 }[/math] have magic sums equal to,

[math]\displaystyle{ M = (b-1) \times \frac {p-1}{2}. }[/math]

The table below lists some prime numbers that generate prime-reciprocal magic squares in given bases.

Prime	Base	Magic sum
19	10	81
53	12	286
59	2	29
67	2	33
83	2	41
89	19	792
211	2	105
223	3	222
307	5	612
383	10	1,719
397	5	792
487	6	1,215
593	3	592
631	87	27,090
787	13	4,716
811	3	810
1,033	11	5,160
1,307	5	2,612
1,499	11	7,490
1,877	19	16,884
2,011	26	25,125
2,027	2	1,013

Full magic squares

The [math]\displaystyle{ \bold{\tfrac {1}{19}} }[/math] magic square with maximum period 18 contains a row-and-column total of 81, that is also obtained by both diagonals. This makes it the first full, non-normal base-10 prime reciprocal magic square whose multiples fit inside respective [math]\displaystyle{ k }[/math]−th rows:

[math]\displaystyle{ \begin{align} 1/19 & = 0. {\color{red}0} \text { } 5 \text { } 2 \text { } 6 \text { } 3 \text { } 1 \text { } 5 \text { } 7 \text { } 8 \text { } 9 \text { } 4 \text { } 7 \text { } 3 \text { } 6 \text { } 8 \text { } 4 \text { } 2 \text { } {\color{red}1} \dots \\ 2/19 & = 0.1 \text { } {\color{red}0} \text { } 5 \text { } 2 \text { } 6 \text { } 3 \text { } 1 \text { } 5 \text { } 7 \text { } 8 \text { } 9 \text { } 4 \text { } 7 \text { } 3 \text { } 6 \text { } 8 \text { } {\color{red}4} \text { } 2 \dots \\ 3/19 & = 0.1 \text { } 5 \text { } {\color{red}7} \text { } 8 \text { } 9 \text { } 4 \text { } 7 \text { } 3 \text { } 6 \text { } 8 \text { } 4 \text { } 2 \text { } 1 \text { } 0 \text { } 5 \text { } {\color{red}2} \text { } 6 \text { } 3 \dots \\ 4/19 & = 0.2 \text { } 1 \text { } 0 \text { } {\color{red}5} \text { } 2 \text { } 6 \text { } 3 \text { } 1 \text { } 5 \text { } 7 \text { } 8 \text { } 9 \text { } 4 \text { } 7 \text { } {\color{red}3} \text { } 6 \text { } 8 \text { } 4 \dots \\ 5/19 & = 0.2 \text { } 6 \text { } 3 \text { } 1 \text { } {\color{red}5} \text { } 7 \text { } 8 \text { } 9 \text { } 4 \text { } 7 \text { } 3 \text { } 6 \text { } 8 \text { } {\color{red}4} \text { } 2 \text { } 1 \text { } 0 \text { } 5 \dots \\ 6/19 & = 0.3 \text { } 1 \text { } 5 \text { } 7 \text { } 8 \text { } {\color{red}9} \text { } 4 \text { } 7 \text { } 3 \text { } 6 \text { } 8 \text { } 4 \text { } {\color{red}2} \text { } 1 \text { } 0 \text { } 5 \text { } 2 \text { } 6 \dots \\ 7/19 & = 0.3 \text { } 6 \text { } 8 \text { } 4 \text { } 2 \text { } 1 \text { } {\color{red}0} \text { } 5 \text { } 2 \text { } 6 \text { } 3 \text { } {\color{red}1} \text { } 5 \text { } 7 \text { } 8 \text { } 9 \text { } 4 \text { } 7 \dots \\ 8/19 & = 0.4 \text { } 2 \text { } 1 \text { } 0 \text { } 5 \text { } 2 \text { } 6 \text { } {\color{red}3} \text { } 1 \text { } 5 \text { } {\color{red}7} \text { } 8 \text { } 9 \text { } 4 \text { } 7 \text { } 3 \text { } 6 \text { } 8 \dots \\ 9/19 & = 0.4 \text { } 7 \text { } 3 \text { } 6 \text { } 8 \text { } 4 \text { } 2 \text { } 1 \text { } {\color{red}0} \text { } {\color{red}5} \text { } 2 \text { } 6 \text { } 3 \text { } 1 \text { } 5 \text { } 7 \text { } 8 \text { } 9 \dots \\ 10/19 & = 0.5 \text { } 2 \text { } 6 \text { } 3 \text { } 1 \text { } 5 \text { } 7 \text { } 8 \text { } {\color{red}9} \text { } {\color{red}4} \text { } 7 \text { } 3 \text { } 6 \text { } 8 \text { } 4 \text { } 2 \text { } 1 \text { } 0 \dots \\ 11/19 & = 0.5 \text { } 7 \text { } 8 \text { } 9 \text { } 4 \text { } 7 \text { } 3 \text { } {\color{red}6} \text { } 8 \text { } 4 \text { } {\color{red}2} \text { } 1 \text { } 0 \text { } 5 \text { } 2 \text { } 6 \text { } 3 \text { } 1 \dots \\ 12/19 & = 0.6 \text { } 3 \text { } 1 \text { } 5 \text { } 7 \text { } 8 \text { } {\color{red}9} \text { } 4 \text { } 7 \text { } 3 \text { } 6 \text { } {\color{red}8} \text { } 4 \text { } 2 \text { } 1 \text { } 0 \text { } 5 \text { } 2 \dots \\ 13/19 & = 0.6 \text { } 8 \text { } 4 \text { } 2 \text { } 1 \text { } {\color{red}0} \text { } 5 \text { } 2 \text { } 6 \text { } 3 \text { } 1 \text { } 5 \text { } {\color{red}7} \text { } 8 \text { } 9 \text { } 4 \text { } 7 \text { } 3 \dots \\ 14/19 & = 0.7 \text { } 3 \text { } 6 \text { } 8 \text { } {\color{red}4} \text { } 2 \text { } 1 \text { } 0 \text { } 5 \text { } 2 \text { } 6 \text { } 3 \text { } 1 \text { } {\color{red}5} \text { } 7 \text { } 8 \text { } 9 \text { } 4 \dots \\ 15/19 & = 0.7 \text { } 8 \text { } 9 \text { } {\color{red}4} \text { } 7 \text { } 3 \text { } 6 \text { } 8 \text { } 4 \text { } 2 \text { } 1 \text { } 0 \text { } 5 \text { } 2 \text { } {\color{red}6} \text { } 3 \text { } 1 \text { } 5 \dots \\ 16/19 & = 0.8 \text { } 4 \text { } {\color{red}2} \text { } 1 \text { } 0 \text { } 5 \text { } 2 \text { } 6 \text { } 3 \text { } 1 \text { } 5 \text { } 7 \text { } 8 \text { } 9 \text { } 4 \text { } {\color{red}7} \text { } 3 \text { } 6 \dots \\ 17/19 & = 0.8 \text { } {\color{red}9} \text { } 4 \text { } 7 \text { } 3 \text { } 6 \text { } 8 \text { } 4 \text { } 2 \text { } 1 \text { } 0 \text { } 5 \text { } 2 \text { } 6 \text { } 3 \text { } 1 \text { } {\color{red}5} \text { } 7 \dots \\ 18/19 & = 0.{\color{red}9} \text { } 4 \text { } 7 \text { } 3 \text { } 6 \text { } 8 \text { } 4 \text { } 2 \text { } 1 \text { } 0 \text { } 5 \text { } 2 \text { } 6 \text { } 3 \text { } 1 \text { } 5 \text { } 7 \text { } {\color{red}8} \dots \\ \end{align} }[/math]

The first few prime numbers in decimal whose reciprocals can be used to produce a non-normal, full prime reciprocal magic square of this type are

{19, 383, 32327, 34061, 45341, 61967, 65699, 117541, 158771, 405817, ...} (sequence A072359 in the OEIS).

The smallest prime number to yield such magic square in binary is 59 (111011₂), while in ternary it is 223 (22021₃); these are listed at A096339, and A096660.

Variations

A [math]\displaystyle{ \tfrac {1}{17} }[/math] prime reciprocal magic square with maximum period of 16 and magic constant of 72 can be constructed where its rows represent non-consecutive multiples of one-seventeenth:

[math]\displaystyle{ \begin{align} 1/17 & = 0.{\color{blue}0} \text { } 5 \; 8 \; 8 \; 2 \; 3 \; 5 \; 2 \; 9 \; 4 \; 1 \; 1 \; 7 \; 6 \; 4 \; {\color{blue}7} \dots \\ 5/17 & = 0.2 \; {\color{blue}9} \; 4 \; 1 \; 1 \; 7 \; 6 \; 4 \; 7 \; 0 \; 5 \; 8 \; 8 \; 2 \; {\color{blue}3} \; 5 \dots \\ 8/17 & = 0.4 \; 7 \; {\color{blue}0} \; 5 \; 8 \; 8 \; 2 \; 3 \; 5 \; 2 \; 9 \; 4 \; 1 \; {\color{blue}1} \; 7 \; 6 \dots \\ 6/17 & = 0.3 \; 5 \; 2 \; {\color{blue}9} \; 4 \; 1 \; 1 \; 7 \; 6 \; 4 \; 7 \; 0 \; {\color{blue}5} \; 8 \; 8 \; 2 \dots \\ 13/17 & = 0.7 \; 6 \; 4 \; 7 \; {\color{blue}0} \; 5 \; 8 \; 8 \; 2 \; 3 \; 5 \; {\color{blue}2} \; 9 \; 4 \; 1 \; 1 \dots \\ 14/17 & = 0.8 \; 2 \; 3 \; 5 \; 2 \; {\color{blue}9} \; 4 \; 1 \; 1 \; 7 \; {\color{blue}6} \; 4 \; 7 \; 0 \; 5 \; 8 \dots \\ 2/17 & = 0.1 \; 1 \; 7 \; 6 \; 4 \; 7 \; {\color{blue}0} \; 5 \; 8 \; {\color{blue}8} \; 2 \; 3 \; 5 \; 2 \; 9 \; 4 \dots \\ 10/17 & = 0.5 \; 8 \; 8 \; 2 \; 3 \; 5 \; 2 \; {\color{blue}9} \; {\color{blue}4} \; 1 \; 1 \; 7 \; 6 \; 4 \; 7 \; 0 \dots \\ 16/17 & = 0.9 \; 4 \; 1 \; 1 \; 7 \; 6 \; 4 \; {\color{blue}7} \; {\color{blue}0} \; 5 \; 8 \; 8 \; 2 \; 3 \; 5 \; 2 \dots \\ 12/17 & = 0.7 \; 0 \; 5 \; 8 \; 8 \; 2 \; {\color{blue}3} \; 5 \; 2 \; {\color{blue}9} \; 4 \; 1 \; 1 \; 7 \; 6 \; 4 \dots \\ 9/17 & = 0.5 \; 2 \; 9 \; 4 \; 1 \; {\color{blue}1} \; 7 \; 6 \; 4 \; 7 \; {\color{blue}0} \; 5 \; 8 \; 8 \; 2 \; 3 \dots \\ 11/17 & = 0.6 \; 4 \; 7 \; 0 \; {\color{blue}5} \; 8 \; 8 \; 2 \; 3 \; 5 \; 2 \; {\color{blue}9} \; 4 \; 1 \; 1 \; 7 \dots \\ 4/17 & = 0.2 \; 3 \; 5 \; {\color{blue}2} \; 9 \; 4 \; 1 \; 1 \; 7 \; 6 \; 4 \; 7 \; {\color{blue}0} \; 5 \; 8 \; 8 \dots \\ 3/17 & = 0.1 \; 7 \; {\color{blue}6} \; 4 \; 7 \; 0 \; 5 \; 8 \; 8 \; 2 \; 3 \; 5 \; 2 \; {\color{blue}9} \; 4 \; 1 \dots \\ 15/17 & = 0.8 \; {\color{blue}8} \; 2 \; 3 \; 5 \; 2 \; 9 \; 4 \; 1 \; 1 \; 7 \; 6 \; 4 \; 7 \; {\color{blue}0} \; 5 \dots \\ 7/17 & = 0.{\color{blue}4} \; 1 \; 1 \; 7 \; 6 \; 4 \; 7 \; 0 \; 5 \; 8 \; 8 \; 2 \; 3 \; 5 \; 2 \; {\color{blue}9} \dots \\ \end{align} }[/math]

As such, this full magic square is the first of its kind in decimal that does not admit a uniform solution where consecutive multiples of [math]\displaystyle{ 1/p }[/math] fit in respective [math]\displaystyle{ k }[/math]−th rows.

See also

• Cyclic number
• Reciprocals of primes