Unit fraction

From HandWiki
Short description: One over a whole number

Slices of approximately 1/8 of a pizza

A unit fraction is a positive fraction with one as its numerator, 1/n. It is the multiplicative inverse (reciprocal) of the denominator of the fraction, which must be a positive natural number. Examples are 1/1, 1/2, 1/3, 1/4, 1/5, etc. When an object is divided into equal parts, each part is a unit fraction of the whole.

Multiplying two unit fractions produces another unit fraction, but other arithmetic operations do not preserve unit fractions. In modular arithmetic, unit fractions can be converted into equivalent whole numbers, allowing modular division to be transformed into multiplication. Every rational number can be represented as a sum of distinct unit fractions; these representations are called Egyptian fractions based on their use in ancient Egyptian mathematics. Many infinite sums of unit fractions are meaningful mathematically.

In geometry, unit fractions can be used to characterize the curvature of triangle groups and the tangencies of Ford circles. Unit fractions are commonly used in fair division, and this familiar application is used in mathematics education as an early step toward the understanding of other fractions. Unit fractions are common in probability theory due to the principle of indifference. They also have applications in combinatorial optimization and in analyzing the pattern of frequencies in the hydrogen spectral series.

Arithmetic

The unit fractions are the rational numbers that can be written in the form [math]\displaystyle{ \frac1n, }[/math] where [math]\displaystyle{ n }[/math] can be any positive natural number. They are thus the multiplicative inverses of the positive integers. When something is divided into [math]\displaystyle{ n }[/math] equal parts, each part is a [math]\displaystyle{ 1/n }[/math] fraction of the whole.[1]

Elementary arithmetic

Multiplying any two unit fractions results in a product that is another unit fraction:[2] [math]\displaystyle{ \frac1x \times \frac1y = \frac1{xy}. }[/math] However, adding,[3] subtracting,[3] or dividing two unit fractions produces a result that is generally not a unit fraction: [math]\displaystyle{ \frac1x + \frac1y = \frac{x+y}{xy} }[/math]

[math]\displaystyle{ \frac1x - \frac1y = \frac{y-x}{xy} }[/math]

[math]\displaystyle{ \frac1x \div \frac1y = \frac{y}{x}. }[/math]

As the last of these formulas shows, every fraction can be expressed as a quotient of two unit fractions.[4]

Modular arithmetic

In modular arithmetic, any unit fraction can be converted into an equivalent whole number using the extended Euclidean algorithm.[5][6] This conversion can be used to perform modular division: dividing by a number [math]\displaystyle{ x }[/math], modulo [math]\displaystyle{ y }[/math], can be performed by converting the unit fraction [math]\displaystyle{ 1/x }[/math] into an equivalent whole number modulo [math]\displaystyle{ y }[/math], and then multiplying by that number.[7]

In more detail, suppose that [math]\displaystyle{ x }[/math] is relatively prime to [math]\displaystyle{ y }[/math] (otherwise, division by [math]\displaystyle{ x }[/math] is not defined modulo [math]\displaystyle{ y }[/math]). The extended Euclidean algorithm for the greatest common divisor can be used to find integers [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] such that Bézout's identity is satisfied: [math]\displaystyle{ \displaystyle ax + by = \gcd(x,y)=1. }[/math] In modulo-[math]\displaystyle{ y }[/math] arithmetic, the term [math]\displaystyle{ by }[/math] can be eliminated as it is zero modulo [math]\displaystyle{ y }[/math]. This leaves [math]\displaystyle{ \displaystyle ax \equiv 1 \pmod y. }[/math] That is, [math]\displaystyle{ a }[/math] is the modular inverse of [math]\displaystyle{ x }[/math], the number that when multiplied by [math]\displaystyle{ x }[/math] produces one. Equivalently,[5][6] [math]\displaystyle{ a \equiv \frac1x \pmod y. }[/math] Thus division by [math]\displaystyle{ x }[/math] (modulo [math]\displaystyle{ y }[/math]) can instead be performed by multiplying by the integer [math]\displaystyle{ a }[/math].[7]

Combinations

Several constructions in mathematics involve combining multiple unit fractions together, often by adding them.

Finite sums

Any positive rational number can be written as the sum of distinct unit fractions, in multiple ways. For example,

[math]\displaystyle{ \frac45=\frac12+\frac14+\frac1{20}=\frac13+\frac15+\frac16+\frac1{10}. }[/math]

These sums are called Egyptian fractions, because the ancient Egyptian civilisations used them as notation for more general rational numbers. There is still interest today in analyzing the methods used by the ancients to choose among the possible representations for a fractional number, and to calculate with such representations.[8] The topic of Egyptian fractions has also seen interest in modern number theory; for instance, the Erdős–Graham conjecture[9] and the Erdős–Straus conjecture[10] concern sums of unit fractions, as does the definition of Ore's harmonic numbers.[11]

A pattern of spherical triangles with reflection symmetry across each triangle edge. Spherical reflection patterns like this with [math]\displaystyle{ 2x }[/math], [math]\displaystyle{ 2y }[/math], and [math]\displaystyle{ 2z }[/math] triangles at each vertex (here, [math]\displaystyle{ x,y,z=2,3,5 }[/math]) only exist when [math]\displaystyle{ \tfrac1x+\tfrac1y+\tfrac1z\gt 1 }[/math].

In geometric group theory, triangle groups are classified into Euclidean, spherical, and hyperbolic cases according to whether an associated sum of unit fractions is equal to one, greater than one, or less than one respectively.[12]

Infinite series

Many well-known infinite series have terms that are unit fractions. These include:

  • The harmonic series, the sum of all positive unit fractions. This sum diverges, and its partial sums [math]\displaystyle{ \frac11 + \frac12 + \frac13 + \cdots + \frac1n }[/math] closely approximate the natural logarithm of [math]\displaystyle{ n }[/math] plus the Euler–Mascheroni constant.[13] Changing every other addition to a subtraction produces the alternating harmonic series, which sums to the natural logarithm of 2:[14] [math]\displaystyle{ \sum_{n = 1}^\infty \frac{(-1)^{n + 1}}{n} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \cdots = \ln 2. }[/math]
  • The Leibniz formula for π is[15] [math]\displaystyle{ 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots = \frac{\pi}{4}. }[/math]
  • The Basel problem concerns the sum of the square unit fractions:[16] [math]\displaystyle{ 1 + \frac14 + \frac19 + \frac1{16} + \cdots = \frac{\pi^2}{6}. }[/math] Similarly, Apéry's constant is an irrational number, the sum of the cubed unit fractions.[17]
  • The binary geometric series is[18] [math]\displaystyle{ 1 + \frac12 + \frac14 + \frac18 + \frac1{16} + \cdots = 2. }[/math]

Matrices

A Hilbert matrix is a square matrix in which the elements on the [math]\displaystyle{ i }[/math]th antidiagonal all equal the unit fraction [math]\displaystyle{ 1/i }[/math]. That is, it has elements [math]\displaystyle{ B_{i,j} = \frac1{i+j-1}. }[/math] For example, the matrix [math]\displaystyle{ \begin{bmatrix} 1 & \frac{1}{2} & \frac{1}{3} \\ \frac{1}{2} & \frac{1}{3} & \frac{1}{4} \\ \frac{1}{3} & \frac{1}{4} & \frac{1}{5} \end{bmatrix} }[/math] is a Hilbert matrix. It has the unusual property that all elements in its inverse matrix are integers.[19] Similarly, (Richardson 2001) defined a matrix whose elements are unit fractions whose denominators are Fibonacci numbers: [math]\displaystyle{ C_{i,j} = \frac1{F_{i+j-1}}, }[/math] where [math]\displaystyle{ F_i }[/math] denotes the [math]\displaystyle{ i }[/math]th Fibonacci number. He calls this matrix the Filbert matrix and it has the same property of having an integer inverse.[20]

Adjacency and Ford circles

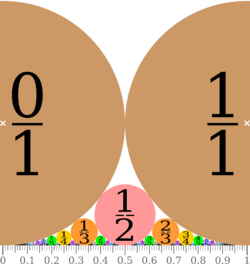
Fractions with tangent Ford circles differ by a unit fraction

Two fractions [math]\displaystyle{ a/b }[/math] and [math]\displaystyle{ c/d }[/math] (in lowest terms) are called adjacent if [math]\displaystyle{ ad-bc=\pm1, }[/math] which implies that they differ from each other by a unit fraction: [math]\displaystyle{ \left|\frac{1}{a}-\frac{1}{b}\right|=\frac{|ad-bc|}{bd}=\frac{1}{bd}. }[/math] For instance, [math]\displaystyle{ \tfrac12 }[/math] and [math]\displaystyle{ \tfrac35 }[/math] are adjacent: [math]\displaystyle{ 1\cdot 5-2\cdot 3=-1 }[/math] and [math]\displaystyle{ \tfrac35-\tfrac12=\tfrac1{10} }[/math]. However, some pairs of fractions whose difference is a unit fraction are not adjacent in this sense: for instance, [math]\displaystyle{ \tfrac13 }[/math] and [math]\displaystyle{ \tfrac23 }[/math] differ by a unit fraction, but are not adjacent, because for them [math]\displaystyle{ ad-bc=3 }[/math].[21]

This terminology comes from the study of Ford circles. These are a system of circles that are tangent to the number line at a given fraction and have the squared denominator of the fraction as their diameter. Fractions [math]\displaystyle{ a/b }[/math] and [math]\displaystyle{ c/d }[/math] are adjacent if and only if their Ford circles are tangent circles.[21]

Applications

Fair division and mathematics education

In mathematics education, unit fractions are often introduced earlier than other kinds of fractions, because of the ease of explaining them visually as equal parts of a whole.[22][23] A common practical use of unit fractions is to divide food equally among a number of people, and exercises in performing this sort of fair division are a standard classroom example in teaching students to work with unit fractions.[24]

Probability and statistics

A six-sided die has probability 1/6 of landing on each side

In a uniform distribution on a discrete space, all probabilities are equal unit fractions. Due to the principle of indifference, probabilities of this form arise frequently in statistical calculations.[25]

Unequal probabilities related to unit fractions arise in Zipf's law. This states that, for many observed phenomena involving the selection of items from an ordered sequence, the probability that the [math]\displaystyle{ n }[/math]th item is selected is proportional to the unit fraction [math]\displaystyle{ 1/n }[/math].[26]

Combinatorial optimization

In the study of combinatorial optimization problems, bin packing problems involve an input sequence of items with fractional sizes, which must be placed into bins whose capacity (the total size of items placed into each bin) is one. Research into these problems has included the study of restricted bin packing problems where the item sizes are unit fractions.[27][28]

One motivation for this is as a test case for more general bin packing methods. Another involves a form of pinwheel scheduling, in which a collection of messages of equal length must each be repeatedly broadcast on a limited number of communication channels, with each message having a maximum delay between the start times of its repeated broadcasts. An item whose delay is [math]\displaystyle{ k }[/math] times the length of a message must occupy a fraction of at least [math]\displaystyle{ 1/k }[/math] of the time slots on the channel it is assigned to, so a solution to the scheduling problem can only come from a solution to the unit fraction bin packing problem with the channels as bins and the fractions [math]\displaystyle{ 1/k }[/math] as item sizes.[27]

Even for bin packing problems with arbitrary item sizes, it can be helpful to round each item size up to the next larger unit fraction, and then apply a bin packing algorithm specialized for unit fraction sizes. In particular, the harmonic bin packing method does exactly this, and then packs each bin using items of only a single rounded unit fraction size.[28]

Physics

The hydrogen spectral series, on a logarithmic scale. The frequencies of the emission lines are proportional to differences of pairs of unit fractions.

The energy levels of photons that can be absorbed or emitted by a hydrogen atom are, according to the Rydberg formula, proportional to the differences of two unit fractions. An explanation for this phenomenon is provided by the Bohr model, according to which the energy levels of electron orbitals in a hydrogen atom are inversely proportional to square unit fractions, and the energy of a photon is quantized to the difference between two levels.[29]

Arthur Eddington argued that the fine-structure constant was a unit fraction. He initially thought it to be 1/136 and later changed his theory to 1/137. This contention has been falsified, given that current estimates of the fine structure constant are (to 6 significant digits) 1/137.036.[30]

See also

  • 17-animal inheritance puzzle, a puzzle involving fair division into unit fractions
  • Submultiple, a number that produces a unit fraction when used as the numerator with a given denominator
  • Superparticular ratio, one plus a unit fraction, important in musical harmony

References

  1. ↑ Cavey, Laurie O.; Kinzel, Margaret T. (February 2014), "From whole numbers to invert and multiply", Teaching Children Mathematics 20 (6): 374–383, doi:10.5951/teacchilmath.20.6.0374 
  2. ↑ Solomon, Pearl Gold (2007), The Math We Need to Know and Do in Grades 6 9: Concepts, Skills, Standards, and Assessments, Corwin Press, p. 157, ISBN 978-1-4129-1726-1, https://books.google.com/books?id=QMWZptwg_d0C&pg=PA157 
  3. ↑ 3.0 3.1 Betz, William (1957), Algebra for Today, First Year, Ginn, p. 370 
  4. ↑ Humenberger, Hans (Fall 2014), "Egyptian fractions – representations as sums of unit fractions", Mathematics and Computer Education 48 (3): 268–283, ProQuest 1622317875 
  5. ↑ 5.0 5.1 Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. "31.4 Solving modular linear equations". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 869–872. ISBN 0-262-03293-7. 
  6. ↑ 6.0 6.1 Goodrich, Michael T.; Tamassia, Roberto (2015), "Section 24.2.2: Modular multiplicative inverses", Algorithm Design and Applications, Wiley, pp. 697–698, ISBN 978-1-118-33591-8 
  7. ↑ 7.0 7.1 Brent, Richard P.; Zimmermann, Paul (2010), "2.5 Modular division and inversion", Modern Computer Arithmetic, Cambridge Monographs on Applied and Computational Mathematics, 18, Cambridge University Press, pp. 65–68, doi:10.1017/cbo9780511921698.001, ISBN 978-1-139-49228-7, https://maths-people.anu.edu.au/~brent/pd/mca-cup-0.5.9.pdf 
  8. ↑ "D11. Egyptian Fractions", Unsolved problems in number theory (3rd ed.), Springer-Verlag, 2004, pp. 252–262, ISBN 978-0-387-20860-2 
  9. ↑ "On a coloring conjecture about unit fractions", Annals of Mathematics 157 (2): 545–556, 2003, doi:10.4007/annals.2003.157.545 
  10. ↑ Elsholtz, Christian (2013), "Counting the number of solutions to the Erdős–Straus equation on unit fractions", Journal of the Australian Mathematical Society 94 (1): 50–105, doi:10.1017/S1446788712000468, https://terrytao.files.wordpress.com/2011/07/egyptian-count13.pdf 
  11. ↑ "On the averages of the divisors of a number", The American Mathematical Monthly 55 (10): 615–619, 1948, doi:10.2307/2305616 
  12. ↑ Noneuclidean Tesselations and their Groups, Pure and Applied Mathematics, 61, Academic Press, 1974, p. 65, ISBN 978-0-08-087377-0, https://books.google.com/books?id=iLkzandfCc8C&pg=PA65 
  13. ↑ "Partial sums of the harmonic series", The American Mathematical Monthly 78 (8): 864–870, 1971, doi:10.1080/00029890.1971.11992881 
  14. ↑ Freniche, Francisco J. (2010), "On Riemann's rearrangement theorem for the alternating harmonic series", The American Mathematical Monthly 117 (5): 442–448, doi:10.4169/000298910X485969, http://eprints.gla.ac.uk/25361/1/id25361.pdf 
  15. ↑ Roy, Ranjan (1990), "The discovery of the series formula for π by Leibniz, Gregory and Nilakantha", Mathematics Magazine 63 (5): 291–306, doi:10.1080/0025570X.1990.11977541, https://www.maa.org/sites/default/files/images/upload_library/22/Allendoerfer/1991/0025570x.di021167.02p0073q.pdf 
  16. ↑ Ayoub, Raymond (1974), "Euler and the zeta function", The American Mathematical Monthly 81 (10): 1067–86, doi:10.2307/2319041, https://www.maa.org/programs/maa-awards/writing-awards/euler-and-the-zeta-function 
  17. ↑ van der Poorten, Alfred (1979), "A proof that Euler missed ... Apéry's proof of the irrationality of [math]\displaystyle{ \zeta(3) }[/math]", The Mathematical Intelligencer 1 (4): 195–203, doi:10.1007/BF03028234, http://www.maths.mq.edu.au/~alf/45.pdf 
  18. ↑ "From Elements of Algebra", The Mathematical Intelligencer 5 (3): 75–76, September 1983, doi:10.1007/bf03026580 
  19. ↑ Choi, Man Duen (1983), "Tricks or treats with the Hilbert matrix", The American Mathematical Monthly 90 (5): 301–312, doi:10.2307/2975779 
  20. ↑ Richardson, Thomas M. (2001), "The Filbert matrix", Fibonacci Quarterly 39 (3): 268–275, Bibcode: 1999math......5079R, http://www.fq.math.ca/Scanned/39-3/richardson.pdf 
  21. ↑ 21.0 21.1 "Fractions", The American Mathematical Monthly 45 (9): 586–601, 1938, doi:10.1080/00029890.1938.11990863 
  22. ↑ Polkinghorne, Ada R. (May 1935), "Young-children and fractions", Childhood Education 11 (8): 354–358, doi:10.1080/00094056.1935.10725374 
  23. ↑ "Unit fractions as superheroes for instruction", The Mathematics Teacher 113 (4): 278–286, April 2020, doi:10.5951/mtlt.2018.0024 
  24. ↑ Wilson, P. Holt; Edgington, Cynthia P.; Nguyen, Kenny H.; Pescosolido, Ryan C.; Confrey, Jere (November 2011), "Fractions: how to fair share", Mathematics Teaching in the Middle School 17 (4): 230–236, doi:10.5951/mathteacmiddscho.17.4.0230 
  25. ↑ Welsh, Alan H. (1996), Aspects of Statistical Inference, Wiley Series in Probability and Statistics, 246, John Wiley and Sons, p. 66, ISBN 978-0-471-11591-5 
  26. ↑ Saichev, Alexander; Malevergne, Yannick; Sornette, Didier (2009), Theory of Zipf's Law and Beyond, Lecture Notes in Economics and Mathematical Systems, 632, Springer-Verlag, ISBN 978-3-642-02945-5 
  27. ↑ 27.0 27.1 Bar-Noy, Amotz (2007), "Windows scheduling as a restricted version of bin packing", ACM Transactions on Algorithms 3 (3): A28:1–A28:22, doi:10.1145/1273340.1273344 
  28. ↑ 28.0 28.1 van Stee, Rob (June 2012), "SIGACT news online algorithms column 20: The power of harmony", ACM SIGACT News 43 (2): 127–136, doi:10.1145/2261417.2261440, https://www.uni-siegen.de/fb6/aan/optimierung/mitarbeiter/vanstee/26.pdf 
  29. ↑ Yang, Fujia; Hamilton, Joseph H. (2009), Modern Atomic and Nuclear Physics, World Scientific, pp. 81–86, ISBN 978-981-283-678-6 
  30. ↑ Kilmister, Clive William (1994), Eddington's Search for a Fundamental Theory: A Key to the Universe, Cambridge University Press, ISBN 978-0-521-37165-0 



Retrieved from "https://handwiki.org/wiki/index.php?title=Unit_fraction&oldid=3712494"