Proofs of Fermat's little theorem

Short description: none

This article collects together a variety of proofs of Fermat's little theorem, which states that

[math]\displaystyle{ a^p \equiv a \pmod p }[/math]

for every prime number p and every integer a (see modular arithmetic).

Simplifications

Some of the proofs of Fermat's little theorem given below depend on two simplifications.

The first is that we may assume that a is in the range 0 ≤ a ≤ p − 1. This is a simple consequence of the laws of modular arithmetic; we are simply saying that we may first reduce a modulo p. This is consistent with reducing [math]\displaystyle{ a^p }[/math] modulo p, as one can check.

Secondly, it suffices to prove that

[math]\displaystyle{ a^{p-1} \equiv 1 \pmod p }[/math]

for a in the range 1 ≤ a ≤ p − 1. Indeed, if the previous assertion holds for such a, multiplying both sides by a yields the original form of the theorem,

[math]\displaystyle{ a^p \equiv a \pmod p }[/math]

On the other hand, if a = 0 or a = 1, the theorem holds trivially.

Combinatorial proofs

Proof by counting necklaces

This is perhaps the simplest known proof, requiring the least mathematical background. It is an attractive example of a combinatorial proof (a proof that involves counting a collection of objects in two different ways).

The proof given here is an adaptation of Golomb's proof.

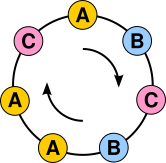
To keep things simple, let us assume that a is a positive integer. Consider all the possible strings of p symbols, using an alphabet with a different symbols. The total number of such strings is a^p since there are a possibilities for each of p positions (see rule of product).

For example, if p = 5 and a = 2, then we can use an alphabet with two symbols (say A and B), and there are 2⁵ = 32 strings of length 5:

AAAAA, AAAAB, AAABA, AAABB, AABAA, AABAB, AABBA, AABBB,

ABAAA, ABAAB, ABABA, ABABB, ABBAA, ABBAB, ABBBA, ABBBB,

BAAAA, BAAAB, BAABA, BAABB, BABAA, BABAB, BABBA, BABBB,

BBAAA, BBAAB, BBABA, BBABB, BBBAA, BBBAB, BBBBA, BBBBB.

We will argue below that if we remove the strings consisting of a single symbol from the list (in our example, AAAAA and BBBBB), the remaining a^p − a strings can be arranged into groups, each group containing exactly p strings. It follows that a^p − a is divisible by p.

Necklaces

Necklace representing seven different strings (ABCBAAC, BCBAACA, CBAACAB, BAACABC, AACABCB, ACABCBA, CABCBAA)

Necklace representing only one string (AAAAAAA)

Let us think of each such string as representing a necklace. That is, we connect the two ends of the string together and regard two strings as the same necklace if we can rotate one string to obtain the second string; in this case we will say that the two strings are friends. In our example, the following strings are all friends:

AAAAB, AAABA, AABAA, ABAAA, BAAAA.

In full, each line of the following list corresponds to a single necklace, and the entire list comprises all 32 strings.

AAAAB, AAABA, AABAA, ABAAA, BAAAA,

AAABB, AABBA, ABBAA, BBAAA, BAAAB,

AABAB, ABABA, BABAA, ABAAB, BAABA,

AABBB, ABBBA, BBBAA, BBAAB, BAABB,

ABABB, BABBA, ABBAB, BBABA, BABAB,

ABBBB, BBBBA, BBBAB, BBABB, BABBB,

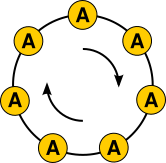
AAAAA,

BBBBB.

Notice that in the above list, each necklace with more than one symbol is represented by 5 different strings, and the number of necklaces represented by just one string is 2, i.e. is the number of distinct symbols. Thus the list shows very clearly why 32 − 2 is divisible by 5.

One can use the following rule to work out how many friends a given string S has:

If S is built up of several copies of the string T, and T cannot itself be broken down further into repeating strings, then the number of friends of S (including S itself) is equal to the length of T.

For example, suppose we start with the string S = ABBABBABBABB, which is built up of several copies of the shorter string T = ABB. If we rotate it one symbol at a time, we obtain the following 3 strings:

ABBABBABBABB,

BBABBABBABBA,

BABBABBABBAB.

There aren't any others because ABB is exactly 3 symbols long and cannot be broken down into further repeating strings.

Completing the proof

Using the above rule, we can complete the proof of Fermat's little theorem quite easily, as follows. Our starting pool of a ^p strings may be split into two categories:

• Some strings contain p identical symbols. There are exactly a of these, one for each symbol in the alphabet. (In our running example, these are the strings AAAAA and BBBBB.)
• The rest of the strings use at least two distinct symbols from the alphabet. If we can break up S into repeating copies of some string T, the length of T must divide the length of S. But since the length of S is the prime p, the only possible length for T is also p. Therefore, the above rule tells us that S has exactly p friends (including S itself).

The second category contains a ^p − a strings, and they may be arranged into groups of p strings, one group for each necklace. Therefore, a ^p − a must be divisible by p, as promised.

Proof using dynamical systems

This proof uses some basic concepts from dynamical systems.

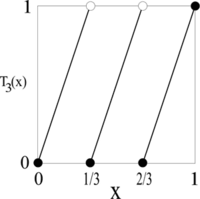
We start by considering a family of functions T_n(x), where n ≥ 2 is an integer, mapping the interval [0, 1] to itself by the formula

[math]\displaystyle{ T_n(x) = \begin{cases} \{ nx \} & 0 \leq x \lt 1, \\ 1 & x = 1, \end{cases} }[/math]

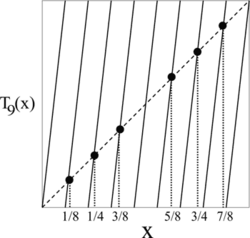
where {y} denotes the fractional part of y. For example, the function T₃(x) is illustrated below:

A number x₀ is said to be a fixed point of a function f(x) if f(x₀) = x₀; in other words, if f leaves x₀ fixed. The fixed points of a function can be easily found graphically: they are simply the x coordinates of the points where the graph of f(x) intersects the graph of the line y = x. For example, the fixed points of the function T₃(x) are 0, 1/2, and 1; they are marked by black circles on the following diagram:

We will require the following two lemmas.

Lemma 1. For any n ≥ 2, the function T_n(x) has exactly n fixed points.

Proof. There are 3 fixed points in the illustration above, and the same sort of geometrical argument applies for any n ≥ 2.

Lemma 2. For any positive integers n and m, and any 0 ≤ x ≤ 1,

[math]\displaystyle{ T_m(T_n(x)) = T_{mn}(x). }[/math]

In other words, T_mn(x) is the composition of T_n(x) and T_m(x).

Proof. The proof of this lemma is not difficult, but we need to be slightly careful with the endpoint x = 1. For this point the lemma is clearly true, since

[math]\displaystyle{ T_m(T_n(1)) = T_m(1) = 1 = T_{mn}(1). }[/math]

So let us assume that 0 ≤ x < 1. In this case,

[math]\displaystyle{ T_n(x) = \{nx\} \lt 1, }[/math]

so T_m(T_n(x)) is given by

[math]\displaystyle{ T_m(T_n(x)) = \{m\{nx\}\}. }[/math]

Therefore, what we really need to show is that

[math]\displaystyle{ \{m\{nx\}\} = \{mnx\}. }[/math]

To do this we observe that {nx} = nx − k, where k is the integer part of nx; then

[math]\displaystyle{ \{m\{nx\}\} = \{mnx - mk\} = \{mnx\}, }[/math]

since mk is an integer.

Now let us properly begin the proof of Fermat's little theorem, by studying the function T_a^p(x). We will assume that a ≥ 2. From Lemma 1, we know that it has a^p fixed points. By Lemma 2 we know that

[math]\displaystyle{ T_{a^p}(x) = \underbrace{T_a(T_a( \cdots T_a(x) \cdots ))}_{p\text{ times}}, }[/math]

so any fixed point of T_a(x) is automatically a fixed point of T_a^p(x).

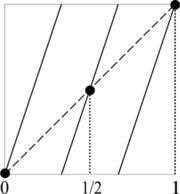
We are interested in the fixed points of T_a^p(x) that are not fixed points of T_a(x). Let us call the set of such points S. There are a^p − a points in S, because by Lemma 1 again, T_a(x) has exactly a fixed points. The following diagram illustrates the situation for a = 3 and p = 2. The black circles are the points of S, of which there are 3² − 3 = 6.

The main idea of the proof is now to split the set S up into its orbits under T_a. What this means is that we pick a point x₀ in S, and repeatedly apply T_a(x) to it, to obtain the sequence of points

[math]\displaystyle{ x_0, T_a(x_0), T_a(T_a(x_0)), T_a(T_a(T_a(x_0))), \ldots. }[/math]

This sequence is called the orbit of x₀ under T_a. By Lemma 2, this sequence can be rewritten as

[math]\displaystyle{ x_0, T_a(x_0), T_{a^2}(x_0), T_{a^3}(x_0), \ldots. }[/math]

Since we are assuming that x₀ is a fixed point of T_{a ^p}(x), after p steps we hit T_a^p(x₀) = x₀, and from that point onwards the sequence repeats itself.

However, the sequence cannot begin repeating itself any earlier than that. If it did, the length of the repeating section would have to be a divisor of p, so it would have to be 1 (since p is prime). But this contradicts our assumption that x₀ is not a fixed point of T_a.

In other words, the orbit contains exactly p distinct points. This holds for every orbit of S. Therefore, the set S, which contains a^p − a points, can be broken up into orbits, each containing p points, so a^p − a is divisible by p.

(This proof is essentially the same as the necklace-counting proof given above, simply viewed through a different lens: one may think of the interval [0, 1] as given by sequences of digits in base a (our distinction between 0 and 1 corresponding to the familiar distinction between representing integers as ending in ".0000..." and ".9999..."). T_aⁿ amounts to shifting such a sequence by n many digits. The fixed points of this will be sequences that are cyclic with period dividing n. In particular, the fixed points of T_a^p can be thought of as the necklaces of length p, with T_aⁿ corresponding to rotation of such necklaces by n spots.

This proof could also be presented without distinguishing between 0 and 1, simply using the half-open interval [0, 1); then T_n would only have n − 1 fixed points, but T_a^p − T_a would still work out to a^p − a, as needed.)

Multinomial proofs

Proof 1

This proof, due to Euler, uses induction to prove the theorem for all integers a ≥ 0.

The base step, that 0^p ≡ 0 (mod p), is trivial. Next, we must show that if the theorem is true for a = k, then it is also true for a = k + 1. For this inductive step, we need the following lemma.

Lemma. For any integers x and y and for any prime p, (x + y)^p ≡ x^p + y^p (mod p).

The lemma is a case of the freshman's dream. Leaving the proof for later on, we proceed with the induction.

Proof. Assume k^p ≡ k (mod p), and consider (k+1)^p. By the lemma we have

[math]\displaystyle{ (k+1)^p \equiv k^p + 1^p \pmod{p}. }[/math]

Using the induction hypothesis, we have that k^p ≡ k (mod p); and, trivially, 1^p = 1. Thus

[math]\displaystyle{ (k+1)^p \equiv k + 1 \pmod{p}, }[/math]

which is the statement of the theorem for a = k+1. ∎

In order to prove the lemma, we must introduce the binomial theorem, which states that for any positive integer n,

[math]\displaystyle{ (x+y)^n=\sum_{i=0}^n{n \choose i}x^{n-i}y^i, }[/math]

where the coefficients are the binomial coefficients,

[math]\displaystyle{ {n \choose i}=\frac{n!}{i!(n-i)!}, }[/math]

described in terms of the factorial function, n! = 1×2×3×⋯×n.

Proof of Lemma. We consider the binomial coefficient when the exponent is a prime p:

[math]\displaystyle{ {p \choose i}=\frac{p!}{i!(p-i)!} }[/math]

The binomial coefficients are all integers. The numerator contains a factor p by the definition of factorial. When 0 < i < p, neither of the terms in the denominator includes a factor of p (relying on the primality of p), leaving the coefficient itself to possess a prime factor of p from the numerator, implying that

[math]\displaystyle{ {p \choose i} \equiv 0 \pmod{p},\qquad 0 \lt i \lt p. }[/math]

Modulo p, this eliminates all but the first and last terms of the sum on the right-hand side of the binomial theorem for prime p. ∎

The primality of p is essential to the lemma; otherwise, we have examples like

[math]\displaystyle{ {4 \choose 2} = 6, }[/math]

which is not divisible by 4.

Proof 2

Using the Lemma, we have:

[math]\displaystyle{ k^p \equiv ((k-1)+1)^p \equiv (k-1)^p + 1 \equiv ((k-2)+1)^p + 1 \equiv (k-2)^p + 2 \equiv \dots \equiv k \pmod{p} }[/math].

Proof using the multinomial expansion

The proof, which was first discovered by Leibniz (who did not publish it) and later rediscovered by Euler, is a very simple application of the multinomial theorem, which states

[math]\displaystyle{ (x_1 + x_2 + \cdots + x_m)^n = \sum_{k_1,k_2,\dots,k_m \atop k_1+k_2+\dots+k_m=n} {n \choose k_1, k_2, \ldots, k_m} x_1^{k_1} x_2^{k_2} \cdots x_m^{k_m} }[/math]

where

[math]\displaystyle{ {n \choose k_1, k_2, \ldots, k_m} = \frac{n!}{k_1! k_2! \dots k_m!} }[/math]

and the summation is taken over all sequences of nonnegative integer indices k₁, k₂, ..., k_m such the sum of all k_i is n.

Thus if we express a as a sum of 1s (ones), we obtain

[math]\displaystyle{ a^p = (1 + 1 + ... + 1)^p = \sum_{k_1,k_2,\dots,k_a \atop k_1+k_2+\dots+k_a=p} {p \choose k_1, k_2, \ldots, k_a} }[/math]

Clearly, if p is prime, and if k_j is not equal to p for any j, we have

[math]\displaystyle{ {p \choose k_1, k_2, \ldots, k_a} \equiv 0 \pmod p, }[/math]

and if k_j is equal to p for some j then

[math]\displaystyle{ {p \choose k_1, k_2, \ldots, k_a} = 1. }[/math]

Since there are exactly a elements such that k_j = p for some j, the theorem follows.

(This proof is essentially a coarser-grained variant of the necklace-counting proof given earlier; the multinomial coefficients count the number of ways a string can be permuted into arbitrary anagrams, while the necklace argument counts the number of ways a string can be rotated into cyclic anagrams. That is to say, that the nontrivial multinomial coefficients here are divisible by p can be seen as a consequence of the fact that each nontrivial necklace of length p can be unwrapped into a string in p many ways.

This multinomial expansion is also, of course, what essentially underlies the binomial theorem-based proof above)

Proof using power product expansions

An additive-combinatorial proof based on formal power product expansions was given by Giedrius Alkauskas. This proof uses neither the Euclidean algorithm nor the binomial theorem, but rather it employs formal power series with rational coefficients.

Proof as a particular case of Euler's theorem

This proof, discovered by James Ivory and rediscovered by Dirichlet requires some background in modular arithmetic.

Let us assume that a is positive and not divisible by p. The idea is that if we write down the sequence of numbers

[math]\displaystyle{ a, 2a, 3a, \ldots, (p-1)a }[/math]

(A)

and reduce each one modulo p, the resulting sequence turns out to be a rearrangement of

[math]\displaystyle{ 1, 2, 3, \ldots, p-1. }[/math]

(B)

Therefore, if we multiply together the numbers in each sequence, the results must be identical modulo p:

[math]\displaystyle{ a \times 2a \times 3a \times \cdots \times (p-1)a \equiv 1 \times 2 \times 3 \times \cdots \times (p-1) \pmod p. }[/math]

Collecting together the a terms yields

[math]\displaystyle{ a^{p-1} (p-1)! \equiv (p-1)! \pmod p. }[/math]

Finally, we may “cancel out” the numbers 1, 2, ..., p − 1 from both sides of this equation, obtaining

[math]\displaystyle{ a^{p-1} \equiv 1 \pmod p. }[/math]

There are two steps in the above proof that we need to justify:

• Why the elements of the sequence (A), reduced modulo p, are a rearrangement of (B), and
• Why it is valid to “cancel” in the setting of modular arithmetic.

We will prove these things below; let us first see an example of this proof in action.

An example

If a = 3 and p = 7, then the sequence in question is

[math]\displaystyle{ 3, 6, 9, 12, 15, 18; }[/math]

reducing modulo 7 gives

[math]\displaystyle{ 3, 6, 2, 5, 1, 4, }[/math]

which is just a rearrangement of

[math]\displaystyle{ 1, 2, 3, 4, 5, 6. }[/math]

Multiplying them together gives

[math]\displaystyle{ 3 \times 6 \times 9 \times 12 \times 15 \times 18 \equiv 3 \times 6 \times 2 \times 5 \times 1 \times 4 \equiv 1 \times 2 \times 3 \times 4 \times 5 \times 6 \pmod 7; }[/math]

that is,

[math]\displaystyle{ 3^6 (1 \times 2 \times 3 \times 4 \times 5 \times 6) \equiv (1 \times 2 \times 3 \times 4 \times 5 \times 6) \pmod 7. }[/math]

Canceling out 1 × 2 × 3 × 4 × 5 × 6 yields

[math]\displaystyle{ 3^6 \equiv 1 \pmod 7, }[/math]

which is Fermat's little theorem for the case a = 3 and p = 7.

The cancellation law

Let us first explain why it is valid, in certain situations, to “cancel”. The exact statement is as follows. If u, x, and y are integers, and u is not divisible by a prime number p, and if

[math]\displaystyle{ ux \equiv uy \pmod p, }[/math]

(C)

then we may “cancel” u to obtain

[math]\displaystyle{ x \equiv y \pmod p. }[/math]

(D)

Our use of this cancellation law in the above proof of Fermat's little theorem was valid because the numbers 1, 2, ..., p − 1 are certainly not divisible by p (indeed they are smaller than p).

We can prove the cancellation law easily using Euclid's lemma, which generally states that if a prime p divides a product ab (where a and b are integers), then p must divide a or b. Indeed, the assertion (C) simply means that p divides ux − uy = u(x − y). Since p is a prime which does not divide u, Euclid's lemma tells us that it must divide x − y instead; that is, (D) holds.

Note that the conditions under which the cancellation law holds are quite strict, and this explains why Fermat's little theorem demands that p is a prime. For example, 2×2 ≡ 2×5 (mod 6), but it is not true that 2 ≡ 5 (mod 6). However, the following generalization of the cancellation law holds: if u, x, y, and z are integers, if u and z are relatively prime, and if

[math]\displaystyle{ ux \equiv uy \pmod z, }[/math]

then we may “cancel” u to obtain

[math]\displaystyle{ x \equiv y \pmod z. }[/math]

This follows from a generalization of Euclid's lemma.

The rearrangement property

Finally, we must explain why the sequence

[math]\displaystyle{ a, 2a, 3a, \ldots, (p-1)a, }[/math]

when reduced modulo p, becomes a rearrangement of the sequence

[math]\displaystyle{ 1, 2, 3, \ldots, p-1. }[/math]

To start with, none of the terms a, 2a, ..., (p − 1)a can be congruent to zero modulo p, since if k is one of the numbers 1, 2, ..., p − 1, then k is relatively prime with p, and so is a, so Euclid's lemma tells us that ka shares no factor with p. Therefore, at least we know that the numbers a, 2a, ..., (p − 1)a, when reduced modulo p, must be found among the numbers 1, 2, 3, ..., p − 1.

Furthermore, the numbers a, 2a, ..., (p − 1)a must all be distinct after reducing them modulo p, because if

[math]\displaystyle{ ka \equiv ma \pmod p, }[/math]

where k and m are one of 1, 2, ..., p − 1, then the cancellation law tells us that

[math]\displaystyle{ k \equiv m \pmod p. }[/math]

Since both k and m are between 1 and p − 1, they must be equal. Therefore, the terms a, 2a, ..., (p − 1)a when reduced modulo p must be distinct. To summarise: when we reduce the p − 1 numbers a, 2a, ..., (p − 1)a modulo p, we obtain distinct members of the sequence 1, 2, ..., p − 1. Since there are exactly p − 1 of these, the only possibility is that the former are a rearrangement of the latter.

Applications to Euler's theorem

This method can also be used to prove Euler's theorem, with a slight alteration in that the numbers from 1 to p − 1 are substituted by the numbers less than and coprime with some number m (not necessarily prime). Both the rearrangement property and the cancellation law (under the generalized form mentioned above) are still satisfied and can be utilized.

For example, if m = 10, then the numbers less than m and coprime with m are 1, 3, 7, and 9. Thus we have:

[math]\displaystyle{ a \times 3a \times 7a \times 9a \equiv 1 \times 3 \times 7 \times 9 \pmod {10}. }[/math]

Therefore,

[math]\displaystyle{ {a^{\varphi(10)}} \equiv 1 \pmod {10}. }[/math]

Proofs using group theory

Standard proof

This proof requires the most basic elements of group theory.

The idea is to recognise that the set G = {1, 2, ..., p − 1}, with the operation of multiplication (taken modulo p), forms a group. The only group axiom that requires some effort to verify is that each element of G is invertible. Taking this on faith for the moment, let us assume that a is in the range 1 ≤ a ≤ p − 1, that is, a is an element of G. Let k be the order of a, that is, k is the smallest positive integer such that a^k ≡ 1 (mod p). Then the numbers 1, a, a², ..., a^k −1 reduced modulo p form a subgroup of G whose order is k and therefore, by Lagrange's theorem, k divides the order of G, which is p − 1. So p − 1 = km for some positive integer m and then

[math]\displaystyle{ a^{p-1} \equiv a^{km} \equiv (a^k)^m \equiv 1^m \equiv 1 \pmod p. }[/math]

To prove that every element b of G is invertible, we may proceed as follows. First, b is coprime to p. Thus Bézout's identity assures us that there are integers x and y such that bx + py = 1. Reading this equality modulo p, we see that x is an inverse for b, since bx ≡ 1 (mod p). Therefore, every element of G is invertible. So, as remarked earlier, G is a group.

For example, when p = 11, the inverses of each element are given as follows:

a	1	2	3	4	5	6	7	8	9	10
a −1	1	6	4	3	9	2	8	7	5	10

Euler's proof

If we take the previous proof and, instead of using Lagrange's theorem, we try to prove it in this specific situation, then we get Euler's third proof, which is the one that he found more natural. Let A be the set whose elements are the numbers 1, a, a², ..., a^k − 1 reduced modulo p. If A = G, then k = p − 1 and therefore k divides p −1. Otherwise, there is some b₁ ∈ G\A.

Let A₁ be the set whose elements are the numbers b₁, ab₁, a²b₁, ..., a^{k − 1}b₁ reduced modulo p. Then A₁ has k distinct elements because otherwise there would be two distinct numbers m, n ∈ {0, 1, ..., k − 1} such that a^mb₁ ≡ aⁿb₁ (mod p), which is impossible, since it would follow that a^m ≡ aⁿ (mod p). On the other hand, no element of A₁ can be an element of A, because otherwise there would be numbers m, n ∈ {0, 1, ..., k − 1} such that a^mb₁ ≡ aⁿ (mod p), and then b₁ ≡ aⁿa^{k − m} ≡ a^{n + k − m} (mod p), which is impossible, since b₁ ∉ A.

So, the set A∪A₁ has 2k elements. If it turns out to be equal to G, then 2k = p −1 and therefore k divides p −1. Otherwise, there is some b₂ ∈ G\(A∪A₁) and we can start all over again, defining A₂ as the set whose elements are the numbers b₂, ab₂, a²b₂, ..., a^k − 1b₂ reduced modulo p. Since G is finite, this process must stop at some point and this proves that k divides p − 1.

For instance, if a = 5 and p = 13, then, since

• 5² = 25 ≡ 12 (mod 13),
• 5³ = 125 ≡ 8 (mod 13),
• 5⁴ = 625 ≡ 1 (mod 13),

we have k = 4 and A = {1, 5, 8, 12}. Clearly, A ≠ G = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. Let b₁ be an element of G\A; for instance, take b₁ = 2. Then, since

• 2×1 = 2,
• 2×5 = 10,
• 2×8 = 16 ≡ 3 (mod 13),
• 2×12 = 24 ≡ 11 (mod 13),

we have A₁ = {2, 3, 10, 11}. Clearly, A∪A₁ ≠ G. Let b₂ be an element of G\(A∪A₁); for instance, take b₂ = 4. Then, since

• 4×1 = 4,
• 4×5 = 20 ≡ 7 (mod 13),
• 4×8 = 32 ≡ 6 (mod 13),
• 4×12 = 48 ≡ 9 (mod 13),

we have A₂ = {4, 6, 7, 9}. And now G = A∪A₁∪A₂.

Note that the sets A, A₁, and so on are in fact the cosets of A in G.