Prosthaphaeresis

From HandWiki
Short description: Approximate multiplication and division using formulas from trigonometry


Prosthaphaeresis (from the Greek προσθαφαίρεσις) was an algorithm used in the late 16th century and early 17th century for approximate multiplication and division using formulas from trigonometry. For the 25 years preceding the invention of the logarithm in 1614, it was the only known generally applicable way of approximating products quickly. Its name comes from the Greek prosthesis (πρόσθεσις) and aphaeresis (ἀφαίρεσις), meaning addition and subtraction, two steps in the process.[1][2]

History and motivation

A spherical triangle

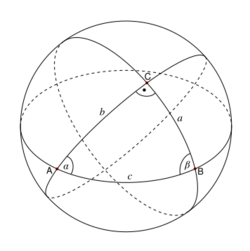
In 16th-century Europe, celestial navigation of ships on long voyages relied heavily on ephemerides to determine their position and course. These voluminous charts prepared by astronomers detailed the position of stars and planets at various points in time. The models used to compute these were based on spherical trigonometry, which relates the angles and arc lengths of spherical triangles (see diagram, right) using formulas such as

[math]\displaystyle{ \cos a = \cos b \cos c + \sin b \sin c \cos \alpha }[/math]

and

[math]\displaystyle{ \sin b \sin \alpha = \sin a \sin \beta, }[/math]

where a, b and c are the angles subtended at the centre of the sphere by the corresponding arcs.

When one quantity in such a formula is unknown but the others are known, the unknown quantity can be computed using a series of multiplications, divisions, and trigonometric table lookups. Astronomers had to make thousands of such calculations, and because the best method of multiplication available was long multiplication, most of this time was spent taxingly multiplying out products.

Mathematicians, particularly those who were also astronomers, were looking for an easier way, and trigonometry was one of the most advanced and familiar fields to these people. Prosthaphaeresis appeared in the 1580s, but its originator is not known for certain;[3] its contributors included the mathematicians Ibn Yunis, Johannes Werner, Paul Wittich, Joost Bürgi, Christopher Clavius, and François Viète. Wittich, Yunis, and Clavius were all astronomers and have all been credited by various sources with discovering the method. Its most well-known proponent was Tycho Brahe, who used it extensively for astronomical calculations such as those described above. It was also used by John Napier, who is credited with inventing the logarithms that would supplant it.

Nicholas Copernicus mentions "prosthaphaeresis" several times in his 1543 work De Revolutionibus Orbium Coelestium, meaning the "great parallax" caused by the displacement of the observer due to the Earth's annual motion.

The identities

The trigonometric identities exploited by prosthaphaeresis relate products of trigonometric functions to sums. They include the following:

[math]\displaystyle{ \begin{align} \sin a \sin b & = \frac{\cos(a - b) - \cos(a + b)}{2} \\[6pt] \cos a \cos b & = \frac{\cos(a - b) + \cos(a + b)}{2} \\[6pt] \sin a \cos b & = \frac{\sin(a + b) + \sin(a - b)}{2} \\[6pt] \cos a \sin b & = \frac{\sin(a + b) - \sin(a - b)}{2} \end{align} }[/math]

The first two of these are believed to have been derived by Jost Bürgi,[citation needed] who related them to [Tycho?] Brahe;[citation needed] the others follow easily from these two. If both sides are multiplied by 2, these formulas are also called the Werner formulas.

The algorithm

Using the second formula above, the technique for multiplication of two numbers works as follows:

  1. Scale down: By shifting the decimal point to the left or right, scale both numbers to values between [math]\displaystyle{ -1 }[/math] and [math]\displaystyle{ 1 }[/math], to be referred to as [math]\displaystyle{ \cos \alpha }[/math] and [math]\displaystyle{ \cos \beta }[/math].
  2. Inverse cosine: Using an inverse cosine table, find two angles [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] whose cosines are our two values.
  3. Sum and difference: Find the sum and difference of the two angles.
  4. Average the cosines: Find the cosines of the sum and difference angles using a cosine table and average them, giving (according to the second formula above) the product [math]\displaystyle{ \cos \alpha \cos \beta }[/math].
  5. Scale up: Shift the decimal place in the answer the combined number of places we have shifted the decimal in the first step for each input, but in the opposite direction.

For example, say we want to multiply [math]\displaystyle{ 105 }[/math] and [math]\displaystyle{ 720 }[/math]. Following the steps:

  1. Scale down: Shift the decimal point three places to the left in each. We get [math]\displaystyle{ \cos \alpha = 0.105 }[/math] and [math]\displaystyle{ \cos \beta = 0.720 }[/math].
  2. Inverse cosine: [math]\displaystyle{ \cos 84^\circ }[/math] is about 0.105, and [math]\displaystyle{ \cos 44^\circ }[/math] is about [math]\displaystyle{ 0.720 }[/math].
  3. Sum and difference: [math]\displaystyle{ 84 + 44 = 128 }[/math], and [math]\displaystyle{ 84 - 44 = 40 }[/math].
  4. Average the cosines: [math]\displaystyle{ \tfrac{1}{2}(\cos 128^\circ + \cos 40^\circ) }[/math] is about [math]\displaystyle{ \tfrac{1}{2}(-0.616 + 0.766) = 0.075 }[/math].
  5. Scale up: For each of [math]\displaystyle{ 105 }[/math] and [math]\displaystyle{ 720 }[/math] we shifted the decimal point three places to the left, so in the answer we shift six places to the right. The result is [math]\displaystyle{ 75\,000 }[/math]. This is very close to the actual product, [math]\displaystyle{ 75\,600 }[/math] (a percent error of ≈0.8%).

If we want the product of the cosines of the two initial values, which is useful in some of the astronomical calculations mentioned above, this is surprisingly even easier: only steps 3 and 4 above are necessary.

To divide, we exploit the definition of the secant as the reciprocal of the cosine. To divide [math]\displaystyle{ 3500 }[/math] by [math]\displaystyle{ 70 }[/math], we scale the numbers to [math]\displaystyle{ 0.35 }[/math] and [math]\displaystyle{ 7.0 }[/math]. The cosine of [math]\displaystyle{ 69.5^\circ }[/math] is [math]\displaystyle{ 0.35 }[/math]. Then use a table of secants to find out that [math]\displaystyle{ 7.0 }[/math] is the secant of [math]\displaystyle{ 81.8^\circ }[/math]. This means that [math]\displaystyle{ 1/7.0 }[/math] is the cosine of [math]\displaystyle{ 81.8^\circ }[/math], and so we can multiply [math]\displaystyle{ 0.35 }[/math] by [math]\displaystyle{ 1/7.0 }[/math] using the above procedure. Average the cosine of the sum of the angles, [math]\displaystyle{ 81.8^\circ + 69.5^\circ = 151.3^\circ }[/math], with the cosine of their difference, [math]\displaystyle{ 81.8^\circ - 69.5^\circ = 12.3^\circ }[/math],

[math]\displaystyle{ \tfrac{1}{2}(\cos 151^\circ + \cos 12.3^\circ) \approx \tfrac{1}{2}(-0.877 + 0.977) = 0.050. }[/math]

Scaling up to locate the decimal point gives the approximate answer, [math]\displaystyle{ 50 }[/math].

Algorithms using the other formulas are similar, but each using different tables (sine, inverse sine, cosine, and inverse cosine) in different places. The first two are the easiest because they each only require two tables. Using the second formula, however, has the unique advantage that if only a cosine table is available, it can be used to estimate inverse cosines by searching for the angle with the nearest cosine value.

Notice how similar the above algorithm is to the process for multiplying using logarithms, which follows these steps: scale down, take logarithms, add, take inverse logarithm, scale up. It is no surprise that the originators of logarithms had used prosthaphaeresis. Indeed the two are closely related mathematically. In modern terms, prosthaphaeresis can be viewed as relying on the logarithm of complex numbers, in particular on Euler's formula

[math]\displaystyle{ e^{ix} = \cos x + i \sin x. }[/math]

Decreasing the error

If all the operations are performed with high precision, the product can be as accurate as desired. Although sums, differences, and averages are easy to compute with high precision, even by hand, trigonometric functions and especially inverse trigonometric functions are not. For this reason, the accuracy of the method depends to a large extent on the accuracy and detail of the trigonometric tables used.

For example, a sine table with an entry for each degree can be off by as much as 0.0087 if we just round an angle off to the nearest degree; each time we double the size of the table (for example, by giving entries for every half-degree instead of every degree) we halve this error. Tables were painstakingly constructed for prosthaphaeresis with values for every second, or 3600th of a degree.

Inverse sine and cosine functions are particularly troublesome, because they become steep near −1 and 1. One solution is to include more table values in this area. Another is to scale the inputs to numbers between −0.9 and 0.9. For example, 950 would become 0.095 instead of 0.950.

Another effective approach to enhancing the accuracy is linear interpolation, which chooses a value between two adjacent table values. For example, if we know that the sine of 45° is about 0.707 and the sine of 46° is about 0.719, we can estimate the sine of 45.7° as 0.707 × (1 − 0.7) + 0.719 × 0.7 = 0.7154. The actual sine is 0.7157. A table of cosines with only 180 entries combined with linear interpolation is as accurate as a table with about 45000 entries without it. Even a quick estimate of the interpolated value is often much closer than the nearest table value. See lookup table for more details.

Reverse identities

The product formulas can also be manipulated to obtain formulas that express addition in terms of multiplication. Although less useful for computing products, these are still useful for deriving trigonometric results:

[math]\displaystyle{ \begin{align} \sin a + \sin b & = 2 \sin \left(\frac{a + b}{2} \right) \cos \left(\frac{a - b}{2} \right) \\[5pt] \sin a - \sin b & = 2 \cos \left(\frac{a + b}{2} \right) \sin \left(\frac{a - b}{2} \right) \\[5pt] \cos a + \cos b & = 2 \cos \left(\frac{a + b}{2} \right) \cos \left(\frac{a - b}{2} \right) \\[5pt] \cos a - \cos b & = -2 \sin \left(\frac{a + b}{2} \right) \sin \left(\frac{a - b}{2} \right) \end{align} }[/math]

See also

References

  1. ↑ Pierce, R. C., Jr. (January 1977). "A Brief History of Logarithms". The Two-Year College Mathematics Journal (Mathematical Association of America) 8 (1): 22–26. doi:10.2307/3026878. 
  2. ↑ Prosthaphaeresis, by Brian Borchers
  3. ↑ Thoren, Victor E. (1988). "Prosthaphaeresis Revisited". Historia Mathematica 15 (1): 32–39. doi:10.1016/0315-0860(88)90047-X. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Prosthaphaeresis&oldid=3375425"