Proximity analysis
Proximity analysis is a class of spatial analysis tools and algorithms that employ geographic distance as a central principle.[1] Distance is fundamental to geographic inquiry and spatial analysis, due to principles such as the friction of distance, Tobler's first law of geography, and Spatial autocorrelation, which are incorporated into analytical tools.[2] Proximity methods are thus used in a variety of applications, especially those that involve movement and interaction.
Distance measures
All proximity analysis tools are based on a measure of distance between two locations. This may seen as a simplistic geometric measurement, but the nature of geographic phenomena and geographic activity requires several candidate methods to measure and express distance and distance-related measures.[2]
- Euclidean distance, the straight-line geometric distance measured on a planar surface. In geographic information systems, this can be easily calculated from locations in a cartesian Projected coordinate system using the Pythagorean theorem. While it is the simplest method to measure distance, it rarely reflects actual geographic movement.
- Manhattan distance, the distance between two locations in a cartesian (planar) coordinate system along a path that only follows the x and y axes (thus appearing similar to a path through a grid street network such as that of Manhattan).
- Geodesic distance, the shortest distance between two locations that stays on the surface of the Earth, following a great circle. On a sphere, the formula uses the spherical law of cosines, but the method is significantly more difficult on an ellipsoid.
- Network distance, a measurement between two locations along a route within a constrained linear space, such as a road or utility network.
- Abstract distance, a measurement of distance in a space that is only indirectly related to geographic space, or only metaphorically spatial. Examples include social networks of interpersonal connections, information spaces of related concepts, and the hypertext network of the World Wide Web. Although these are not inherently geographic, projecting them into an abstract space allows geographic tools such as proximity analysis to be used to study them.[3]
- Cost distance, a measurement along a route (in any of the above spaces) in which geometric distance is replaced by some other quantity that accumulates along the route (and is thus proportional to distance), called a cost because it generally serves as an undesirable quantity to be minimized.[4] Travel time is the most common cost measurement, but other costs include carbon emissions, fuel consumption, environmental impacts, and construction costs.
Techniques
There are a variety of tools, models, and algorithms that incorporate geographic distance, due to the variety of relevant problems and tasks.[5]

- Buffers, a tool for determining the region that is within a specified distance of a set of geographic features.
- Cost distance analysis, algorithms for finding optimal routes through continuous space that minimize distance and/or other location dependent costs.[4]
- Voronoi diagram, also known as Thiessen polygons, an algorithm for partitioning continuous space into a set of regions based on a set of point locations, such that each region consists of locations that are closer to one of the points than any others.[6]
- Distance decay, based on the Inverse square law, a mathematical model of how the influence of a phenomenon tends to be inversely proportional to the distance from it. A Gravity model is a similar model.
- Location analysis, a set of (usually heuristic) algorithms for finding the optimal locations of a limited set of points (e.g., store locations) that minimize the aggregate distance to another set of points (e.g., customer locations). A commonly used example is Lloyd's algorithm.
- Distance matrix, an array containing the distances (Euclidean or otherwise) between any two points in a set. This is frequently used as the independent variable in statistical tests of whether the strength of a relationship is correlated with distance, such as the volume of trade between cities.
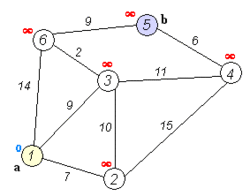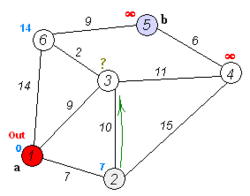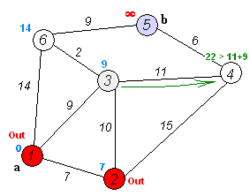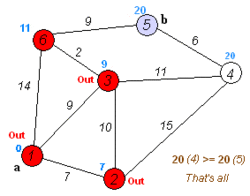
- Transport network analysis, a set of algorithms and tools for solving a number of distance routing problems when travel is constrained to a network of one-dimensional lines, such as roads and utility networks.[7] For example, the common task of finding the shortest route from point A to point B, which is typically solved using Dijkstra's algorithm
References
- ↑ Blinn, Charles R., Lloyd P. Queen, and Les W. Maki, "Geographic Information Systems: A Glossary."
- ↑ 2.0 2.1 Sarkar, D.. "FC-42 - Distance Operations". UCGIS. https://gistbok.ucgis.org/bok-topics/distance-operations.
- ↑ Agarwal, Pragya; Skupin, André (2008). Self-organizing maps: Applications in geographic information science. Wiley. ISBN 9780470021675.
- ↑ 4.0 4.1 "How cost distance tools work". Esri. https://pro.arcgis.com/en/pro-app/latest/tool-reference/spatial-analyst/how-the-cost-distance-tools-work.htm.
- ↑ de Smith, Michael J.; Goodchild, Michael F.; Longley, Paul A. (2018). "4.4 Distance Operations". Geospatial Analysis: A Comprehensive Guide to Principles, Techniques, and Software Tools (6th ed.). https://www.spatialanalysisonline.com/HTML/index.html?distance_operations.htm.
- ↑ "25.1.18.81 Voronoi polygons". OSGEO. https://docs.qgis.org/3.22/en/docs/user_manual/processing_algs/qgis/vectorgeometry.html#voronoi-polygons.
- ↑ "Network Analyst solvers". Esri. https://pro.arcgis.com/en/pro-app/latest/help/analysis/networks/network-analyst-solver-types.htm.
External links
- Proximity tools in Esri ArcGIS
- OGC ST_DWithin function (PostGIS implementation)
 |
