Dijkstra's algorithm
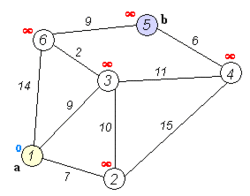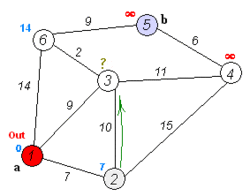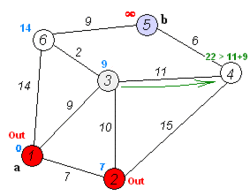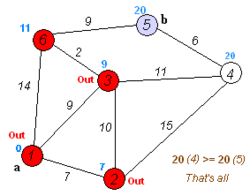 Dijkstra's algorithm to find the shortest path between a and b. It picks the unvisited vertex with the lowest distance, calculates the distance through it to each unvisited neighbor, and updates the neighbor's distance if smaller. Mark visited (set to red) when done with neighbors. | |
| Class | Search algorithm Greedy algorithm Dynamic programming[1] |
|---|---|
| Data structure | Graph Usually used with priority queue or heap for optimization[2][3] |
| Worst-case performance | [math]\displaystyle{ \Theta(|E| + |V| \log|V|) }[/math][3] |
Dijkstra's algorithm (/ˈdaɪkstrəz/ DYKE-strəz) is an algorithm for finding the shortest paths between nodes in a weighted graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.[4][5][6]
The algorithm exists in many variants. Dijkstra's original algorithm found the shortest path between two given nodes,[6] but a more common variant fixes a single node as the "source" node and finds shortest paths from the source to all other nodes in the graph, producing a shortest-path tree.
For a given source node in the graph, the algorithm finds the shortest path between that node and every other.[7]:196–206 It can also be used for finding the shortest paths from a single node to a single destination node by stopping the algorithm once the shortest path to the destination node has been determined. For example, if the nodes of the graph represent cities and costs of edge paths represent driving distances between pairs of cities connected by a direct road (for simplicity, ignore red lights, stop signs, toll roads and other obstructions), then Dijkstra's algorithm can be used to find the shortest route between one city and all other cities. A widely used application of shortest path algorithms is network routing protocols, most notably IS-IS (Intermediate System to Intermediate System) and OSPF (Open Shortest Path First). It is also employed as a subroutine in other algorithms such as Johnson's.
The Dijkstra algorithm uses labels that are positive integers or real numbers, which are totally ordered. It can be generalized to use any labels that are partially ordered, provided the subsequent labels (a subsequent label is produced when traversing an edge) are monotonically non-decreasing. This generalization is called the generic Dijkstra shortest-path algorithm.[8][9]
Dijkstra's algorithm uses a data structure for storing and querying partial solutions sorted by distance from the start. Dijkstra's original algorithm does not use a min-priority queue and runs in time [math]\displaystyle{ \Theta(|V|^2) }[/math](where [math]\displaystyle{ |V| }[/math] is the number of nodes).[10] The idea of this algorithm is also given in Leyzorek et al. 1957. Fredman & Tarjan 1984 propose using a Fibonacci heap min-priority queue to optimize the running time complexity to [math]\displaystyle{ \Theta(|E|+|V|\log|V|) }[/math]. This is asymptotically the fastest known single-source shortest-path algorithm for arbitrary directed graphs with unbounded non-negative weights. However, specialized cases (such as bounded/integer weights, directed acyclic graphs etc.) can indeed be improved further as detailed in Specialized variants. Additionally, if preprocessing is allowed algorithms such as contraction hierarchies can be up to seven orders of magnitude faster.
In some fields, artificial intelligence in particular, Dijkstra's algorithm or a variant of it is known as uniform cost search and formulated as an instance of the more general idea of best-first search.[11]
History
What is the shortest way to travel from Rotterdam to Groningen, in general: from given city to given city. It is the algorithm for the shortest path, which I designed in about twenty minutes. One morning I was shopping in Amsterdam with my young fiancée, and tired, we sat down on the café terrace to drink a cup of coffee and I was just thinking about whether I could do this, and I then designed the algorithm for the shortest path. As I said, it was a twenty-minute invention. In fact, it was published in '59, three years later. The publication is still readable, it is, in fact, quite nice. One of the reasons that it is so nice was that I designed it without pencil and paper. I learned later that one of the advantages of designing without pencil and paper is that you are almost forced to avoid all avoidable complexities. Eventually, that algorithm became to my great amazement, one of the cornerstones of my fame.—Edsger Dijkstra, in an interview with Philip L. Frana, Communications of the ACM, 2001[5]
Dijkstra thought about the shortest path problem when working at the Mathematical Center in Amsterdam in 1956 as a programmer to demonstrate the capabilities of a new computer called ARMAC.[12] His objective was to choose both a problem and a solution (that would be produced by computer) that non-computing people could understand. He designed the shortest path algorithm and later implemented it for ARMAC for a slightly simplified transportation map of 64 cities in the Netherlands (64, so that 6 bits would be sufficient to encode the city number).[5] A year later, he came across another problem from hardware engineers working on the institute's next computer: minimize the amount of wire needed to connect the pins on the back panel of the machine. As a solution, he re-discovered the algorithm known as Prim's minimal spanning tree algorithm (known earlier to Jarník, and also rediscovered by Prim).[13][14] Dijkstra published the algorithm in 1959, two years after Prim and 29 years after Jarník.[15][16]
Algorithm

Let the node at which we are starting be called the initial node. Let the distance of node Y be the distance from the initial node to Y. Dijkstra's algorithm will initially start with infinite distances and will try to improve them step by step.
- Mark all nodes unvisited. Create a set of all the unvisited nodes called the unvisited set.
- Assign to every node a tentative distance value: set it to zero for our initial node and to infinity for all other nodes. During the run of the algorithm, the tentative distance of a node v is the length of the shortest path discovered so far between the node v and the starting node. Since initially no path is known to any other vertex than the source itself (which is a path of length zero), all other tentative distances are initially set to infinity. Set the initial node as current.[17]
- For the current node, consider all of its unvisited neighbors and calculate their tentative distances through the current node. Compare the newly calculated tentative distance to the one currently assigned to the neighbor and assign it the smaller one. For example, if the current node A is marked with a distance of 6, and the edge connecting it with a neighbor B has length 2, then the distance to B through A will be 6 + 2 = 8. If B was previously marked with a distance greater than 8 then change it to 8. Otherwise, the current value will be kept.
- When we are done considering all of the unvisited neighbors of the current node, mark the current node as visited and remove it from the unvisited set. A visited node will never be checked again (this is valid and optimal in connection with the behavior in step 6.: that the next nodes to visit will always be in the order of 'smallest distance from initial node first' so any visits after would have a greater distance).
- If the destination node has been marked visited (when planning a route between two specific nodes) or if the smallest tentative distance among the nodes in the unvisited set is infinity (when planning a complete traversal; occurs when there is no connection between the initial node and remaining unvisited nodes), then stop. The algorithm has finished.
- Otherwise, select the unvisited node that is marked with the smallest tentative distance, set it as the new current node, and go back to step 3.
When planning a route, it is actually not necessary to wait until the destination node is "visited" as above: the algorithm can stop once the destination node has the smallest tentative distance among all "unvisited" nodes (and thus could be selected as the next "current").
Description
Suppose you would like to find the shortest path between two intersections on a city map: a starting point and a destination. Dijkstra's algorithm initially marks the distance (from the starting point) to every other intersection on the map with infinity. This is done not to imply that there is an infinite distance, but to note that those intersections have not been visited yet. Some variants of this method leave the intersections' distances unlabeled. Now select the current intersection at each iteration. For the first iteration, the current intersection will be the starting point, and the distance to it (the intersection's label) will be zero. For subsequent iterations (after the first), the current intersection will be a closest unvisited intersection to the starting point (this will be easy to find).
From the current intersection, update the distance to every unvisited intersection that is directly connected to it. This is done by determining the sum of the distance between an unvisited intersection and the value of the current intersection and then relabeling the unvisited intersection with this value (the sum) if it is less than the unvisited intersection's current value. In effect, the intersection is relabeled if the path to it through the current intersection is shorter than the previously known paths. To facilitate shortest path identification, in pencil, mark the road with an arrow pointing to the relabeled intersection if you label/relabel it, and erase all others pointing to it. After you have updated the distances to each neighboring intersection, mark the current intersection as visited and select an unvisited intersection with minimal distance (from the starting point) – or the lowest label—as the current intersection. Intersections marked as visited are labeled with the shortest path from the starting point to it and will not be revisited or returned to.
Continue this process of updating the neighboring intersections with the shortest distances, marking the current intersection as visited, and moving onto a closest unvisited intersection until you have marked the destination as visited. Once you have marked the destination as visited (as is the case with any visited intersection), you have determined the shortest path to it from the starting point and can trace your way back following the arrows in reverse. In the algorithm's implementations, this is usually done (after the algorithm has reached the destination node) by following the nodes' parents from the destination node up to the starting node; that's why we also keep track of each node's parent.
This algorithm makes no attempt of direct "exploration" towards the destination as one might expect. Rather, the sole consideration in determining the next "current" intersection is its distance from the starting point. This algorithm therefore expands outward from the starting point, interactively considering every node that is closer in terms of shortest path distance until it reaches the destination. When understood in this way, it is clear how the algorithm necessarily finds the shortest path. However, it may also reveal one of the algorithm's weaknesses: its relative slowness in some topologies.
Pseudocode
In the following pseudocode algorithm, dist is an array that contains the current distances from the source to other vertices, i.e. dist[u] is the current distance from the source to the vertex u. The prev array contains pointers to previous-hop nodes on the shortest path from source to the given vertex (equivalently, it is the next-hop on the path from the given vertex to the source). The code u ← vertex in Q with min dist[u], searches for the vertex u in the vertex set Q that has the least dist[u] value. Graph.Edges(u, v) returns the length of the edge joining (i.e. the distance between) the two neighbor-nodes u and v. The variable alt on line 14 is the length of the path from the root node to the neighbor node v if it were to go through u. If this path is shorter than the current shortest path recorded for v, that current path is replaced with this alt path.[7]
1 function Dijkstra(Graph, source): 2 3 for each vertex v in Graph.Vertices: 4 dist[v] ← INFINITY 5 prev[v] ← UNDEFINED 6 add v to Q 7 dist[source] ← 0 8 9 while Q is not empty: 10 u ← vertex in Q with min dist[u] 11 remove u from Q 12 13 for each neighbor v of u still in Q: 14 alt ← dist[u] + Graph.Edges(u, v) 15 if alt < dist[v]: 16 dist[v] ← alt 17 prev[v] ← u 18 19 return dist[], prev[]
If we are only interested in a shortest path between vertices source and target, we can terminate the search after line 10 if u = target. Now we can read the shortest path from source to target by reverse iteration:
1 S ← empty sequence 2 u ← target 3 if prev[u] is defined or u = source: // Do something only if the vertex is reachable 4 while u is defined: // Construct the shortest path with a stack S 5 insert u at the beginning of S // Push the vertex onto the stack 6 u ← prev[u] // Traverse from target to source
Now sequence S is the list of vertices constituting one of the shortest paths from source to target, or the empty sequence if no path exists.
A more general problem would be to find all the shortest paths between source and target (there might be several different ones of the same length). Then instead of storing only a single node in each entry of prev[] we would store all nodes satisfying the relaxation condition. For example, if both r and source connect to target and both of them lie on different shortest paths through target (because the edge cost is the same in both cases), then we would add both r and source to prev[target]. When the algorithm completes, prev[] data structure will actually describe a graph that is a subset of the original graph with some edges removed. Its key property will be that if the algorithm was run with some starting node, then every path from that node to any other node in the new graph will be the shortest path between those nodes in the original graph, and all paths of that length from the original graph will be present in the new graph. Then to actually find all these shortest paths between two given nodes we would use a path finding algorithm on the new graph, such as depth-first search.
Using a priority queue
A min-priority queue is an abstract data type that provides 3 basic operations: add_with_priority(), decrease_priority() and extract_min(). As mentioned earlier, using such a data structure can lead to faster computing times than using a basic queue. Notably, Fibonacci heap[18] or Brodal queue offer optimal implementations for those 3 operations. As the algorithm is slightly different, it is mentioned here, in pseudocode as well:
1 function Dijkstra(Graph, source): 2 dist[source] ← 0 // Initialization 3 4 create vertex priority queue Q 5 6 for each vertex v in Graph.Vertices: 7 if v ≠ source 8 dist[v] ← INFINITY // Unknown distance from source to v 9 prev[v] ← UNDEFINED // Predecessor of v 10 11 Q.add_with_priority(v, dist[v]) 12 13 14 while Q is not empty: // The main loop 15 u ← Q.extract_min() // Remove and return best vertex 16 for each neighbor v of u: // Go through all v neighbors of u 17 alt ← dist[u] + Graph.Edges(u, v) 18 if alt < dist[v]: 19 dist[v] ← alt 20 prev[v] ← u 21 Q.decrease_priority(v, alt) 22 23 return dist, prev
Instead of filling the priority queue with all nodes in the initialization phase, it is also possible to initialize it to contain only source; then, inside the if alt < dist[v] block, the decrease_priority() becomes an add_with_priority() operation if the node is not already in the queue.[7]:198
Yet another alternative is to add nodes unconditionally to the priority queue and to instead check after extraction that it isn't revisiting, or that no shorter connection was found yet. This can be done by additionally extracting the associated priority p from the queue and only processing further if p == dist[u] inside the while Q is not empty loop. [19]
These alternatives can use entirely array-based priority queues without decrease-key functionality, which have been found to achieve even faster computing times in practice. However, the difference in performance was found to be narrower for denser graphs.[20]
Proof of correctness
Proof of Dijkstra's algorithm is constructed by induction on the number of visited nodes.
Invariant hypothesis: For each visited node v, dist[v] is the shortest distance from source to v, and for each unvisited node u, dist[u] is the shortest distance from source to u when traveling via visited nodes only, or infinity if no such path exists. (Note: we do not assume dist[u] is the actual shortest distance for unvisited nodes, while dist[v] is the actual shortest distance)
The base case is when there is just one visited node, namely the initial node source, in which case the hypothesis is trivial.
Next, assume the hypothesis for k-1 visited nodes. Next, we choose u to be the next visited node according to the algorithm. We claim that dist[u] is the shortest distance from source to u.
To prove that claim, we will proceed with a proof by contradiction. If there were a shorter path, then there can be two cases, either the shortest path contains another unvisited node or not.
In the first case, let w be the first unvisited node on the shortest path. By the induction hypothesis, the shortest path from source to u and w through visited node only has cost dist[u] and dist[w] respectively. That means the cost of going from source to u through w has the cost of at least dist[w] + the minimal cost of going from w to u. As the edge costs are positive, the minimal cost of going from w to u is a positive number.
Also dist[u] < dist[w] because the algorithm picked u instead of w.
Now we arrived at a contradiction that dist[u] < dist[w] yet dist[w] + a positive number < dist[u].
In the second case, let w be the last but one node on the shortest path. That means dist[w] + Graph.Edges[w,u] < dist[u]. That is a contradiction because by the time w is visited, it should have set dist[u] to at most dist[w] + Graph.Edges[w,u].
For all other visited nodes v, the induction hypothesis told us dist[v] is the shortest distance from source already, and the algorithm step is not changing that.
After processing u it will still be true that for each unvisited node w, dist[w] will be the shortest distance from source to w using visited nodes only because if there were a shorter path that doesn't go by u we would have found it previously, and if there were a shorter path using u we would have updated it when processing u.
After all nodes are visited, the shortest path from source to any node v consists only of visited nodes, therefore dist[v] is the shortest distance.
Running time
Bounds of the running time of Dijkstra's algorithm on a graph with edges E and vertices V can be expressed as a function of the number of edges, denoted [math]\displaystyle{ |E| }[/math], and the number of vertices, denoted [math]\displaystyle{ |V| }[/math], using big-O notation. The complexity bound depends mainly on the data structure used to represent the set Q. In the following, upper bounds can be simplified because [math]\displaystyle{ |E| }[/math] is [math]\displaystyle{ O(|V|^2) }[/math] for any simple graph, but that simplification disregards the fact that in some problems, other upper bounds on [math]\displaystyle{ |E| }[/math] may hold.
For any data structure for the vertex set Q, the running time is in[2]
- [math]\displaystyle{ \Theta(|E| \cdot T_\mathrm{dk} + |V| \cdot T_\mathrm{em}), }[/math]
where [math]\displaystyle{ T_\mathrm{dk} }[/math] and [math]\displaystyle{ T_\mathrm{em} }[/math] are the complexities of the decrease-key and extract-minimum operations in Q, respectively.
The simplest version of Dijkstra's algorithm stores the vertex set Q as a linked list or array, and edges as an adjacency list or matrix. In this case, extract-minimum is simply a linear search through all vertices in Q, so the running time is [math]\displaystyle{ \Theta(|E| + |V|^2) = \Theta(|V|^2) }[/math].
For sparse graphs, that is, graphs with far fewer than [math]\displaystyle{ |V|^2 }[/math] edges, Dijkstra's algorithm can be implemented more efficiently by storing the graph in the form of adjacency lists and using a self-balancing binary search tree, binary heap, pairing heap, or Fibonacci heap as a priority queue to implement extracting minimum efficiently. To perform decrease-key steps in a binary heap efficiently, it is necessary to use an auxiliary data structure that maps each vertex to its position in the heap, and to keep this structure up to date as the priority queue Q changes. With a self-balancing binary search tree or binary heap, the algorithm requires
- [math]\displaystyle{ \Theta((|E| + |V|) \log |V|) }[/math]
time in the worst case; for connected graphs this time bound can be simplified to [math]\displaystyle{ \Theta( | E | \log | V | ) }[/math]. The Fibonacci heap improves this to
- [math]\displaystyle{ \Theta(|E| + |V| \log|V|). }[/math]
When using binary heaps, the average case time complexity is lower than the worst-case: assuming edge costs are drawn independently from a common probability distribution, the expected number of decrease-key operations is bounded by [math]\displaystyle{ \Theta(|V| \log (|E|/|V|)) }[/math], giving a total running time of[7]:199–200
- [math]\displaystyle{ O\left(|E| + |V| \log \frac{|E|}{|V|} \log |V|\right). }[/math]
Practical optimizations and infinite graphs
In common presentations of Dijkstra's algorithm, initially all nodes are entered into the priority queue. This is, however, not necessary: the algorithm can start with a priority queue that contains only one item, and insert new items as they are discovered (instead of doing a decrease-key, check whether the key is in the queue; if it is, decrease its key, otherwise insert it).[7]:198 This variant has the same worst-case bounds as the common variant, but maintains a smaller priority queue in practice, speeding up the queue operations.[11]
Moreover, not inserting all nodes in a graph makes it possible to extend the algorithm to find the shortest path from a single source to the closest of a set of target nodes on infinite graphs or those too large to represent in memory. The resulting algorithm is called uniform-cost search (UCS) in the artificial intelligence literature[11][21][22] and can be expressed in pseudocode as
procedure uniform_cost_search(start) is
node ← start
frontier ← priority queue containing node only
expanded ← empty set
do
if frontier is empty then
return failure
node ← frontier.pop()
if node is a goal state then
return solution(node)
expanded.add(node)
for each of node's neighbors n do
if n is not in expanded and not in frontier then
frontier.add(n)
else if n is in frontier with higher cost
replace existing node with n
The complexity of this algorithm can be expressed in an alternative way for very large graphs: when C* is the length of the shortest path from the start node to any node satisfying the "goal" predicate, each edge has cost at least ε, and the number of neighbors per node is bounded by b, then the algorithm's worst-case time and space complexity are both in O(b1+⌊C* ⁄ ε⌋).[21]
Further optimizations of Dijkstra's algorithm for the single-target case include bidirectional variants, goal-directed variants such as the A* algorithm (see § Related problems and algorithms), graph pruning to determine which nodes are likely to form the middle segment of shortest paths (reach-based routing), and hierarchical decompositions of the input graph that reduce s–t routing to connecting s and t to their respective "transit nodes" followed by shortest-path computation between these transit nodes using a "highway".[23] Combinations of such techniques may be needed for optimal practical performance on specific problems.[24]
Specialized variants
When arc weights are small integers (bounded by a parameter [math]\displaystyle{ C }[/math]), specialized queues which take advantage of this fact can be used to speed up Dijkstra's algorithm. The first algorithm of this type was Dial's algorithm (Dial 1969) for graphs with positive integer edge weights, which uses a bucket queue to obtain a running time [math]\displaystyle{ O(|E|+|V|C) }[/math]. The use of a Van Emde Boas tree as the priority queue brings the complexity to [math]\displaystyle{ O(|E|\log\log C) }[/math] (Ahuja Mehlhorn). Another interesting variant based on a combination of a new radix heap and the well-known Fibonacci heap runs in time [math]\displaystyle{ O(|E|+|V|\sqrt{\log C}) }[/math] (Ahuja Mehlhorn). Finally, the best algorithms in this special case are as follows. The algorithm given by (Thorup 2000) runs in [math]\displaystyle{ O(|E|\log\log|V|) }[/math] time and the algorithm given by (Raman 1997) runs in [math]\displaystyle{ O(|E| + |V|\min\{(\log|V|)^{1/3+\varepsilon}, (\log C)^{1/4+\varepsilon}\}) }[/math] time.
Related problems and algorithms
The functionality of Dijkstra's original algorithm can be extended with a variety of modifications. For example, sometimes it is desirable to present solutions which are less than mathematically optimal. To obtain a ranked list of less-than-optimal solutions, the optimal solution is first calculated. A single edge appearing in the optimal solution is removed from the graph, and the optimum solution to this new graph is calculated. Each edge of the original solution is suppressed in turn and a new shortest-path calculated. The secondary solutions are then ranked and presented after the first optimal solution.
Dijkstra's algorithm is usually the working principle behind link-state routing protocols, OSPF and IS-IS being the most common ones.
Unlike Dijkstra's algorithm, the Bellman–Ford algorithm can be used on graphs with negative edge weights, as long as the graph contains no negative cycle reachable from the source vertex s. The presence of such cycles means there is no shortest path, since the total weight becomes lower each time the cycle is traversed. (This statement assumes that a "path" is allowed to repeat vertices. In graph theory that is normally not allowed. In theoretical computer science it often is allowed.) It is possible to adapt Dijkstra's algorithm to handle negative weight edges by combining it with the Bellman-Ford algorithm (to remove negative edges and detect negative cycles); such an algorithm is called Johnson's algorithm.
The A* algorithm is a generalization of Dijkstra's algorithm that cuts down on the size of the subgraph that must be explored, if additional information is available that provides a lower bound on the "distance" to the target.
The process that underlies Dijkstra's algorithm is similar to the greedy process used in Prim's algorithm. Prim's purpose is to find a minimum spanning tree that connects all nodes in the graph; Dijkstra is concerned with only two nodes. Prim's does not evaluate the total weight of the path from the starting node, only the individual edges.
Breadth-first search can be viewed as a special-case of Dijkstra's algorithm on unweighted graphs, where the priority queue degenerates into a FIFO queue.
The fast marching method can be viewed as a continuous version of Dijkstra's algorithm which computes the geodesic distance on a triangle mesh.
Dynamic programming perspective
From a dynamic programming point of view, Dijkstra's algorithm is a successive approximation scheme that solves the dynamic programming functional equation for the shortest path problem by the Reaching method.[25][26][27]
In fact, Dijkstra's explanation of the logic behind the algorithm,[28] namely
Problem 2. Find the path of minimum total length between two given nodes [math]\displaystyle{ P }[/math] and [math]\displaystyle{ Q }[/math].
We use the fact that, if [math]\displaystyle{ R }[/math] is a node on the minimal path from [math]\displaystyle{ P }[/math] to [math]\displaystyle{ Q }[/math], knowledge of the latter implies the knowledge of the minimal path from [math]\displaystyle{ P }[/math] to [math]\displaystyle{ R }[/math].
is a paraphrasing of Bellman's famous Principle of Optimality in the context of the shortest path problem.
See also
- A* search algorithm
- Bellman–Ford algorithm
- Euclidean shortest path
- Floyd–Warshall algorithm
- Johnson's algorithm
- Longest path problem
- Parallel all-pairs shortest path algorithm
Notes
- ↑ Controversial, see Moshe Sniedovich (2006). "Dijkstra's algorithm revisited: the dynamic programming connexion". Control and Cybernetics 35: 599–620. https://www.infona.pl/resource/bwmeta1.element.baztech-article-BAT5-0013-0005/tab/summary. and below part.
- ↑ 2.0 2.1 Cormen et al. 2001
- ↑ 3.0 3.1 Fredman & Tarjan 1987
- ↑ Richards, Hamilton. "Edsger Wybe Dijkstra". Association for Computing Machinery. http://amturing.acm.org/award_winners/dijkstra_1053701.cfm. "At the Mathematical Centre a major project was building the ARMAC computer. For its official inauguration in 1956, Dijkstra devised a program to solve a problem interesting to a nontechnical audience: Given a network of roads connecting cities, what is the shortest route between two designated cities?"
- ↑ 5.0 5.1 5.2 Frana, Phil (August 2010). "An Interview with Edsger W. Dijkstra". Communications of the ACM 53 (8): 41–47. doi:10.1145/1787234.1787249.
- ↑ 6.0 6.1 Dijkstra, E. W. (1959). "A note on two problems in connexion with graphs". Numerische Mathematik 1: 269–271. doi:10.1007/BF01386390. https://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=40368327ACB1D1FFF45671886D563916?doi=10.1.1.165.7577&rep=rep1&type=pdf.
- ↑ 7.0 7.1 7.2 7.3 7.4 Mehlhorn, Kurt; Sanders, Peter (2008). "Chapter 10. Shortest Paths". Algorithms and Data Structures: The Basic Toolbox. Springer. doi:10.1007/978-3-540-77978-0. ISBN 978-3-540-77977-3. http://people.mpi-inf.mpg.de/~mehlhorn/ftp/Toolbox/ShortestPaths.pdf.
- ↑ Szcześniak, Ireneusz; Jajszczyk, Andrzej; Woźna-Szcześniak, Bożena (2019). "Generic Dijkstra for optical networks". Journal of Optical Communications and Networking 11 (11): 568–577. doi:10.1364/JOCN.11.000568.
- ↑ Szcześniak, Ireneusz; Woźna-Szcześniak, Bożena (2023), "Generic Dijkstra: Correctness and tractability", NOMS 2023-2023 IEEE/IFIP Network Operations and Management Symposium, pp. 1–7, doi:10.1109/NOMS56928.2023.10154322, ISBN 978-1-6654-7716-1
- ↑ Schrijver, Alexander (2012). "On the history of the shortest path problem.". Documenta Mathematica. http://ftp.gwdg.de/pub/misc/EMIS/journals/DMJDMV/vol-ismp/32_schrijver-alexander-sp.pdf.
- ↑ 11.0 11.1 11.2 Felner, Ariel (2011). "Position Paper: Dijkstra's Algorithm versus Uniform Cost Search or a Case Against Dijkstra's Algorithm". Proc. 4th Int'l Symp. on Combinatorial Search. http://www.aaai.org/ocs/index.php/SOCS/SOCS11/paper/view/4017/4357. In a route-finding problem, Felner finds that the queue can be a factor 500–600 smaller, taking some 40% of the running time.
- ↑ "ARMAC". 2007. http://www-set.win.tue.nl/UnsungHeroes/machines/armac.html.
- ↑ Dijkstra, Edsger W., Reflections on "A note on two problems in connexion with graphs, https://www.cs.utexas.edu/users/EWD/ewd08xx/EWD841a.PDF
- ↑ Tarjan, Robert Endre (1983), Data Structures and Network Algorithms, CBMS_NSF Regional Conference Series in Applied Mathematics, 44, Society for Industrial and Applied Mathematics, p. 75, "The third classical minimum spanning tree algorithm was discovered by Jarník and rediscovered by Prim and Dikstra; it is commonly known as Prim's algorithm."
- ↑ Prim, R.C. (1957). "Shortest connection networks and some generalizations". Bell System Technical Journal 36 (6): 1389–1401. doi:10.1002/j.1538-7305.1957.tb01515.x. Bibcode: 1957BSTJ...36.1389P. http://bioinfo.ict.ac.cn/~dbu/AlgorithmCourses/Lectures/Prim1957.pdf. Retrieved 18 July 2017.
- ↑ V. Jarník: O jistém problému minimálním [About a certain minimal problem], Práce Moravské Přírodovědecké Společnosti, 6, 1930, pp. 57–63. (in Czech)
- ↑ Gass, Saul; Fu, Michael (2013). Gass, Saul I; Fu, Michael C. eds. Encyclopedia of Operations Research and Management Science. 1. Springer. doi:10.1007/978-1-4419-1153-7. ISBN 978-1-4419-1137-7.
- ↑ Fredman & Tarjan 1984.
- ↑ Observe that p < dist[u] cannot ever hold because of the update dist[v] ← alt when updating the queue. See https://cs.stackexchange.com/questions/118388/dijkstra-without-decrease-key for discussion.
- ↑ Chen, M.; Chowdhury, R. A.; Ramachandran, V.; Roche, D. L.; Tong, L. (2007). Priority Queues and Dijkstra's Algorithm – UTCS Technical Report TR-07-54 – 12 October 2007. Austin, Texas: The University of Texas at Austin, Department of Computer Sciences. http://www.cs.sunysb.edu/~rezaul/papers/TR-07-54.pdf.
- ↑ 21.0 21.1 Russell, Stuart; Norvig, Peter (2009) [1995]. Artificial Intelligence: A Modern Approach (3rd ed.). Prentice Hall. pp. 75, 81. ISBN 978-0-13-604259-4.
- ↑ Sometimes also least-cost-first search: Nau, Dana S. (1983). "Expert computer systems". Computer (IEEE) 16 (2): 63–85. doi:10.1109/mc.1983.1654302. https://www.cs.umd.edu/~nau/papers/nau1983expert.pdf.
- ↑ Wagner, Dorothea; Willhalm, Thomas (2007). "Speed-up techniques for shortest-path computations". STACS. pp. 23–36.
- ↑ Bauer, Reinhard; Delling, Daniel; Sanders, Peter; Schieferdecker, Dennis; Schultes, Dominik; Wagner, Dorothea (2010). "Combining hierarchical and goal-directed speed-up techniques for Dijkstra's algorithm". J. Experimental Algorithmics 15: 2.1. doi:10.1145/1671970.1671976. https://publikationen.bibliothek.kit.edu/1000014952.
- ↑ Sniedovich, M. (2006). "Dijkstra's algorithm revisited: the dynamic programming connexion". Journal of Control and Cybernetics 35 (3): 599–620. http://matwbn.icm.edu.pl/ksiazki/cc/cc35/cc3536.pdf. Online version of the paper with interactive computational modules.
- ↑ Denardo, E.V. (2003). Dynamic Programming: Models and Applications. Mineola, NY: Dover Publications. ISBN 978-0-486-42810-9.
- ↑ Sniedovich, M. (2010). Dynamic Programming: Foundations and Principles. Francis & Taylor. ISBN 978-0-8247-4099-3.
- ↑ Dijkstra 1959, p. 270
References
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "Section 24.3: Dijkstra's algorithm". Introduction to Algorithms (Second ed.). MIT Press and McGraw–Hill. pp. 595–601. ISBN 0-262-03293-7.
- Dial, Robert B. (1969). "Algorithm 360: Shortest-path forest with topological ordering [H]". Communications of the ACM 12 (11): 632–633. doi:10.1145/363269.363610.
- Fredman, Michael Lawrence; Tarjan, Robert E. (1984). "Fibonacci heaps and their uses in improved network optimization algorithms". 25th Annual Symposium on Foundations of Computer Science. IEEE. pp. 338–346. doi:10.1109/SFCS.1984.715934.
- Fredman, Michael Lawrence; Tarjan, Robert E. (1987). "Fibonacci heaps and their uses in improved network optimization algorithms". Journal of the Association for Computing Machinery 34 (3): 596–615. doi:10.1145/28869.28874.
- Zhan, F. Benjamin; Noon, Charles E. (February 1998). "Shortest Path Algorithms: An Evaluation Using Real Road Networks". Transportation Science 32 (1): 65–73. doi:10.1287/trsc.32.1.65.
- Leyzorek, M.; Gray, R. S.; Johnson, A. A.; Ladew, W. C.; Meaker, Jr., S. R.; Petry, R. M.; Seitz, R. N. (1957). Investigation of Model Techniques – First Annual Report – 6 June 1956 – 1 July 1957 – A Study of Model Techniques for Communication Systems. Cleveland, Ohio: Case Institute of Technology.
- Knuth, D.E. (1977). "A Generalization of Dijkstra's Algorithm". Information Processing Letters 6 (1): 1–5. doi:10.1016/0020-0190(77)90002-3.
- Ahuja, Ravindra K.; Mehlhorn, Kurt; Orlin, James B.; Tarjan, Robert E. (April 1990). "Faster Algorithms for the Shortest Path Problem". Journal of the ACM 37 (2): 213–223. doi:10.1145/77600.77615. https://dspace.mit.edu/bitstream/1721.1/47994/1/fasteralgorithms00sloa.pdf.
- Raman, Rajeev (1997). "Recent results on the single-source shortest paths problem". SIGACT News 28 (2): 81–87. doi:10.1145/261342.261352.
- Thorup, Mikkel (2000). "On RAM priority Queues". SIAM Journal on Computing 30 (1): 86–109. doi:10.1137/S0097539795288246.
- Thorup, Mikkel (1999). "Undirected single-source shortest paths with positive integer weights in linear time". Journal of the ACM 46 (3): 362–394. doi:10.1145/316542.316548. http://www.diku.dk/~mthorup/PAPERS/sssp.ps.gz.
External links
- Oral history interview with Edsger W. Dijkstra, Charles Babbage Institute, University of Minnesota, Minneapolis
- Implementation of Dijkstra's algorithm using TDD, Robert Cecil Martin, The Clean Code Blog
 |