Pseudoconvex function

In convex analysis and the calculus of variations, both branches of mathematics, a pseudoconvex function is a function that behaves like a convex function with respect to finding its local minima, but need not actually be convex. Informally, a differentiable function is pseudoconvex if it is increasing in any direction where it has a positive directional derivative. The property must hold in all of the function domain, and not only for nearby points.

Formal definition

Consider a differentiable function [math]\displaystyle{ f:X \subseteq \mathbb{R}^{n} \rightarrow \mathbb{R} }[/math], defined on a (nonempty) convex open set [math]\displaystyle{ X }[/math] of the finite-dimensional Euclidean space [math]\displaystyle{ \mathbb{R}^n }[/math]. This function is said to be pseudoconvex if the following property holds:

for all [math]\displaystyle{ x,y \in X: \quad \nabla f(x) \cdot (y-x) \geq 0 \Rightarrow f(y) \geq f(x) }[/math].

Equivalently:

for all [math]\displaystyle{ x,y \in X: \quad f(y) \lt f(x) \Rightarrow \nabla f(x) \cdot (y-x) \lt 0 }[/math].

Here [math]\displaystyle{ \nabla f }[/math] is the gradient of [math]\displaystyle{ f }[/math], defined by: [math]\displaystyle{ \nabla f = \left(\frac{\partial f}{\partial x_1},\dots,\frac{\partial f}{\partial x_n}\right). }[/math]

Note that the definition may also be stated in terms of the directional derivative of [math]\displaystyle{ f }[/math], in the direction given by the vector [math]\displaystyle{ v=y-x }[/math]. This is because, as [math]\displaystyle{ f }[/math] is differentiable, this directional derivative is given by:

[math]\displaystyle{ \frac{\partial f}{\partial v}(x) = \nabla f(x) \cdot v = \nabla f(x) \cdot (y-x). }[/math]

Properties

Relation to other types of "convexity"

Every convex function is pseudoconvex, but the converse is not true. For example, the function [math]\displaystyle{ f(x) = x + x^{3} }[/math] is pseudoconvex but not convex. Similarly, any pseudoconvex function is quasiconvex; but the converse is not true, since the function [math]\displaystyle{ f(x) = x^{3} }[/math] is quasiconvex but not pseudoconvex. This can be summarized schematically as:

convex [math]\displaystyle{ \Rightarrow }[/math] pseudoconvex [math]\displaystyle{ \Rightarrow }[/math] quasiconvex

Functions x^3 (quasiconvex but not pseudoconvex) and x^3 + x (pseudoconvex and thus quasiconvex). None of them is convex.

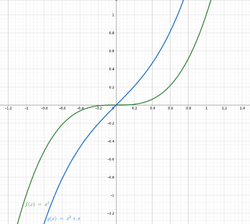
To see that [math]\displaystyle{ f(x) = x^{3} }[/math] is not pseudoconvex, consider its derivative at [math]\displaystyle{ x = 0 }[/math]: [math]\displaystyle{ f^{\prime}(0) = 0 }[/math]. Then, if [math]\displaystyle{ f(x) = x^{3} }[/math] was pseudoconvex, we should have:

[math]\displaystyle{ f^{\prime}(0) (y-0) = 0 \geq 0 \Rightarrow f(y) \geq f(0), \quad \forall \, y \in \mathbb{R}. }[/math]

In particular it should be true for [math]\displaystyle{ y=-1 }[/math]. But it is not, as: [math]\displaystyle{ f(-1) = (-1)^{3} = -1 \lt f(0) = 0 }[/math].

Sufficient optimality condition

For any differentiable function, we have the Fermat's theorem necessary condition of optimality, which states that: if [math]\displaystyle{ f }[/math] has a local minimum at [math]\displaystyle{ x^{*} }[/math] in an open domain, then [math]\displaystyle{ x^{*} }[/math] must be a stationary point of [math]\displaystyle{ f }[/math] (that is: [math]\displaystyle{ \nabla f(x^{*}) = 0 }[/math]).

Pseudoconvexity is of great interest in the area of optimization, because the converse is also true for any pseudoconvex function. That is: if [math]\displaystyle{ x^{*} }[/math] is a stationary point of a pseudoconvex function [math]\displaystyle{ f }[/math], then [math]\displaystyle{ f }[/math] has a global minimum at [math]\displaystyle{ x^{*} }[/math]. Note also that the result guarantees a global minimum (not only local).

This last result is also true for a convex function, but it is not true for a quasiconvex function. Consider for example the quasiconvex function:

[math]\displaystyle{ f(x)=\frac{e^{x}}{x^{2}+1} + \frac{1}{e^{x}} }[/math].

This function is not pseudoconvex, but it is quasiconvex. Also, the point [math]\displaystyle{ x=0 }[/math] is a critical point of [math]\displaystyle{ f }[/math], as [math]\displaystyle{ f^{\prime}(0)=0 }[/math]. However, [math]\displaystyle{ f }[/math] does not have a global minimum at [math]\displaystyle{ x=0 }[/math] (not even a local minimum).

Example of a quasiconvex function that is not pseudoconvex. The function has a critical point at [math]\displaystyle{ x=0 }[/math], but this is not a minimum.

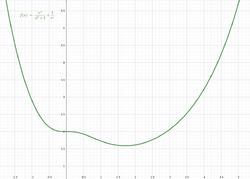
Finally, note that a pseudoconvex function may not have any critical point. Take for example the pseudoconvex function: [math]\displaystyle{ f(x)=x^{3}+x }[/math], whose derivative is always positive: [math]\displaystyle{ f^{\prime}(x)=3x^{2}+1\gt 0, \, \forall \, x \in \mathbb{R} }[/math].

Examples

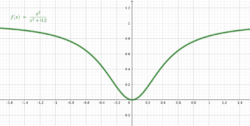
An example of a function that is pseudoconvex, but not convex, is: [math]\displaystyle{ f(x)=\frac{x^{2}}{x^{2}+k}, \, k \gt 0. }[/math] The figure shows this function for the case where [math]\displaystyle{ k=0.2 }[/math]. This example may be generalized to two variables as:

[math]\displaystyle{ f(x)=\frac{x^{2}+y^{2}}{x^{2}+y^{2}+k}, \, k \gt 0. }[/math]

Pseudoconvex function that is not convex.

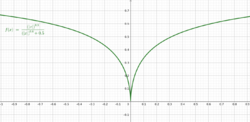
The previous example may be modified to obtain a function that is not convex, nor pseudoconvex, but is quasiconvex:

[math]\displaystyle{ f(x)=\frac{|x|^{p}}{|x|^{p}+k}, \, k \gt 0, \, p \in (0,1). }[/math]

The figure shows this function for the case where [math]\displaystyle{ k=0.5, p=0.6 }[/math]. As can be seen, this function is not convex because of the concavity, and it is not pseudoconvex because it is not differentiable at [math]\displaystyle{ x=0 }[/math].

Quasiconvex function that is not convex, nor pseudoconvex.

Generalization to nondifferentiable functions

The notion of pseudoconvexity can be generalized to nondifferentiable functions as follows. Given any function [math]\displaystyle{ f:X \rightarrow \mathbb{R} }[/math], we can define the upper Dini derivative of [math]\displaystyle{ f }[/math] by:

[math]\displaystyle{ f^{+}(x,u) = \limsup_{ h \to 0^{+} } \frac{f(x+hu) - f(x)}{h}; }[/math]

where u is any unit vector. The function is said to be pseudoconvex if it is increasing in any direction where the upper Dini derivative is positive. More precisely, this is characterized in terms of the subdifferential [math]\displaystyle{ \partial f }[/math] as follows:

For all [math]\displaystyle{ x, y \in X }[/math]: if [math]\displaystyle{ x^* \in \partial f(x) }[/math] is such that [math]\displaystyle{ \langle x^* , y - x \rangle \geq 0 }[/math], then [math]\displaystyle{ f(x) \leq f(z) }[/math], for all [math]\displaystyle{ z \in [x,y] }[/math];

where [math]\displaystyle{ [x,y] }[/math] denotes the line segment adjoining x and y.

Related notions

A pseudoconcave function is a function whose negative is pseudoconvex. A pseudolinear function is a function that is both pseudoconvex and pseudoconcave. For example, linear–fractional programs have pseudolinear objective functions and linear–inequality constraints. These properties allow fractional-linear problems to be solved by a variant of the simplex algorithm (of George B. Dantzig).

Given a vector-valued function [math]\displaystyle{ \eta }[/math], there is a more general notion of [math]\displaystyle{ \eta }[/math]-pseudoconvexity and [math]\displaystyle{ \eta }[/math]-pseudolinearity; wherein classical pseudoconvexity and pseudolinearity pertain to the case when [math]\displaystyle{ \eta (x, y) = y - x }[/math].

See also

• Pseudoconvexity
• Convex function
• Quasiconvex function
• Invex function

References

• Floudas, Christodoulos A.; Pardalos, Panos M. (2001), "Generalized monotone multivalued maps", Encyclopedia of Optimization, Springer, p. 227, ISBN 978-0-7923-6932-5 .
• Mangasarian, O. L. (January 1965). "Pseudo-Convex Functions". Journal of the Society for Industrial and Applied Mathematics, Series A 3 (2): 281–290. doi:10.1137/0303020. ISSN 0363-0129. .
• Rapcsak, T. (1991-02-15). "On pseudolinear functions". European Journal of Operational Research 50 (3): 353–360. doi:10.1016/0377-2217(91)90267-Y. ISSN 0377-2217.