Stationary point

Short description: Zero of the derivative of a function

The stationary points are the red circles. In this graph, they are all relative maxima or relative minima. The blue squares are inflection points.

In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of the function where the function's derivative is zero. Informally, it is a point where the function "stops" increasing or decreasing (hence the name).

For a differentiable function of several real variables, a stationary point is a point on the surface of the graph where all its partial derivatives are zero (equivalently, the gradient is zero).

Stationary points are easy to visualize on the graph of a function of one variable: they correspond to the points on the graph where the tangent is horizontal (i.e., parallel to the x-axis). For a function of two variables, they correspond to the points on the graph where the tangent plane is parallel to the xy plane.

Turning points

A turning point is a point at which the derivative changes sign. A turning point may be either a relative maximum or a relative minimum (also known as local minimum and maximum). If the function is differentiable, then a turning point is a stationary point; however not all stationary points are turning points. If the function is twice differentiable, the stationary points that are not turning points are horizontal inflection points. For example, the function [math]\displaystyle{ x \mapsto x^3 }[/math] has a stationary point at x = 0, which is also an inflection point, but is not a turning point.

Classification

A graph in which local extrema and global extrema have been labeled.

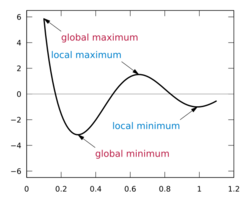
Isolated stationary points of a [math]\displaystyle{ C^1 }[/math] real valued function [math]\displaystyle{ f\colon \mathbb{R} \to \mathbb{R} }[/math] are classified into four kinds, by the first derivative test:

• a local minimum (minimal turning point or relative minimum) is one where the derivative of the function changes from negative to positive;
• a local maximum (maximal turning point or relative maximum) is one where the derivative of the function changes from positive to negative;

Saddle points (stationary points that are neither local maxima nor minima: they are inflection points. The left is a "rising point of inflection" (derivative is positive on both sides of the red point); the right is a "falling point of inflection" (derivative is negative on both sides of the red point).

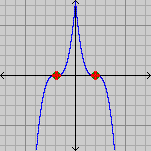
• a rising point of inflection (or inflexion) is one where the derivative of the function is positive on both sides of the stationary point; such a point marks a change in concavity;
• a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary point; such a point marks a change in concavity.

The first two options are collectively known as "local extrema". Similarly a point that is either a global (or absolute) maximum or a global (or absolute) minimum is called a global (or absolute) extremum. The last two options—stationary points that are not local extremum—are known as saddle points.

By Fermat's theorem, global extrema must occur (for a [math]\displaystyle{ C^1 }[/math] function) on the boundary or at stationary points.

Curve sketching

Determining the position and nature of stationary points aids in curve sketching of differentiable functions. Solving the equation f'(x) = 0 returns the x-coordinates of all stationary points; the y-coordinates are trivially the function values at those x-coordinates. The specific nature of a stationary point at x can in some cases be determined by examining the second derivative f''(x):

• If f''(x) < 0, the stationary point at x is concave down; a maximal extremum.
• If f''(x) > 0, the stationary point at x is concave up; a minimal extremum.
• If f''(x) = 0, the nature of the stationary point must be determined by way of other means, often by noting a sign change around that point.

A more straightforward way of determining the nature of a stationary point is by examining the function values between the stationary points (if the function is defined and continuous between them).

A simple example of a point of inflection is the function f(x) = x³. There is a clear change of concavity about the point x = 0, and we can prove this by means of calculus. The second derivative of f is the everywhere-continuous 6x, and at x = 0, f′′ = 0, and the sign changes about this point. So x = 0 is a point of inflection.

More generally, the stationary points of a real valued function [math]\displaystyle{ f\colon \mathbb{R}^{n} \to \mathbb{R} }[/math] are those points x₀ where the derivative in every direction equals zero, or equivalently, the gradient is zero.

Example

For the function f(x) = x⁴ we have f'(0) = 0 and f''(0) = 0. Even though f''(0) = 0, this point is not a point of inflection. The reason is that the sign of f'(x) changes from negative to positive.

For the function f(x) = sin(x) we have f'(0) ≠ 0 and f''(0) = 0. But this is not a stationary point, rather it is a point of inflection. This is because the concavity changes from concave downwards to concave upwards and the sign of f'(x) does not change; it stays positive.

For the function f(x) = x³ we have f'(0) = 0 and f''(0) = 0. This is both a stationary point and a point of inflection. This is because the concavity changes from concave downwards to concave upwards and the sign of f'(x) does not change; it stays positive.

See also

• Optimization (mathematics)
• Fermat's theorem
• Derivative test
• Fixed point (mathematics)
• Saddle point

External links

• Inflection Points of Fourth Degree Polynomials — a surprising appearance of the golden ratio at cut-the-knot