Q-function
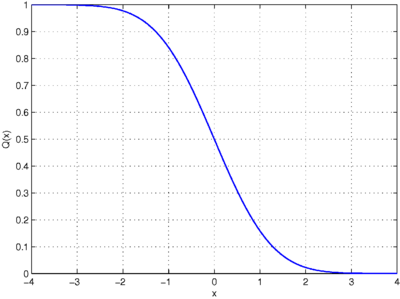
In statistics, the Q-function is the tail distribution function of the standard normal distribution.[1][2] In other words, [math]\displaystyle{ Q(x) }[/math] is the probability that a normal (Gaussian) random variable will obtain a value larger than [math]\displaystyle{ x }[/math] standard deviations. Equivalently, [math]\displaystyle{ Q(x) }[/math] is the probability that a standard normal random variable takes a value larger than [math]\displaystyle{ x }[/math].
If [math]\displaystyle{ Y }[/math] is a Gaussian random variable with mean [math]\displaystyle{ \mu }[/math] and variance [math]\displaystyle{ \sigma^2 }[/math], then [math]\displaystyle{ X = \frac{Y-\mu}{\sigma} }[/math] is standard normal and
- [math]\displaystyle{ P(Y \gt y) = P(X \gt x) = Q(x) }[/math]
where [math]\displaystyle{ x = \frac{y-\mu}{\sigma} }[/math].
Other definitions of the Q-function, all of which are simple transformations of the normal cumulative distribution function, are also used occasionally.[3]
Because of its relation to the cumulative distribution function of the normal distribution, the Q-function can also be expressed in terms of the error function, which is an important function in applied mathematics and physics.
Definition and basic properties
Formally, the Q-function is defined as
- [math]\displaystyle{ Q(x) = \frac{1}{\sqrt{2\pi}} \int_x^\infty \exp\left(-\frac{u^2}{2}\right) \, du. }[/math]
Thus,
- [math]\displaystyle{ Q(x) = 1 - Q(-x) = 1 - \Phi(x)\,\!, }[/math]
where [math]\displaystyle{ \Phi(x) }[/math] is the cumulative distribution function of the standard normal Gaussian distribution.
The Q-function can be expressed in terms of the error function, or the complementary error function, as[2]
- [math]\displaystyle{ \begin{align} Q(x) &=\frac{1}{2}\left( \frac{2}{\sqrt{\pi}} \int_{x/\sqrt{2}}^\infty \exp\left(-t^2\right) \, dt \right)\\ &= \frac{1}{2} - \frac{1}{2} \operatorname{erf} \left( \frac{x}{\sqrt{2}} \right) ~~\text{ -or-}\\ &= \frac{1}{2}\operatorname{erfc} \left(\frac{x}{\sqrt{2}} \right). \end{align} }[/math]
An alternative form of the Q-function known as Craig's formula, after its discoverer, is expressed as:[4]
- [math]\displaystyle{ Q(x) = \frac{1}{\pi} \int_0^{\frac{\pi}{2}} \exp \left( - \frac{x^2}{2 \sin^2 \theta} \right) d\theta. }[/math]
This expression is valid only for positive values of x, but it can be used in conjunction with Q(x) = 1 − Q(−x) to obtain Q(x) for negative values. This form is advantageous in that the range of integration is fixed and finite.
Craig's formula was later extended by Behnad (2020)[5] for the Q-function of the sum of two non-negative variables, as follows:
- [math]\displaystyle{ Q(x+y) = \frac{1}{\pi} \int_0^{\frac{\pi}{2}} \exp \left( - \frac{x^2}{2 \sin^2 \theta} - \frac{y^2}{2 \cos^2 \theta} \right) d\theta, \quad x,y \geqslant 0 . }[/math]
Bounds and approximations
- The Q-function is not an elementary function. However, it can be upper and lower bounded as,[6][7]
- [math]\displaystyle{ \left (\frac{x}{1+x^2} \right ) \phi(x) \lt Q(x) \lt \frac{\phi(x)}{x}, \qquad x\gt 0, }[/math]
- where [math]\displaystyle{ \phi(x) }[/math] is the density function of the standard normal distribution, and the bounds become increasingly tight for large x.
- Using the substitution v =u2/2, the upper bound is derived as follows:
- [math]\displaystyle{ Q(x) =\int_x^\infty\phi(u)\,du \lt \int_x^\infty\frac ux\phi(u)\,du =\int_{\frac{x^2}{2}}^\infty\frac{e^{-v}}{x\sqrt{2\pi}}\,dv=-\biggl.\frac{e^{-v}}{x\sqrt{2\pi}}\biggr|_{\frac{x^2}{2}}^\infty=\frac{\phi(x)}{x}. }[/math]
- Similarly, using [math]\displaystyle{ \phi'(u) = - u \phi(u) }[/math] and the quotient rule,
- [math]\displaystyle{ \left(1+\frac1{x^2}\right)Q(x) =\int_x^\infty \left(1+\frac1{x^2}\right)\phi(u)\,du \gt \int_x^\infty \left(1+\frac1{u^2}\right)\phi(u)\,du =-\biggl.\frac{\phi(u)}u\biggr|_x^\infty =\frac{\phi(x)}x. }[/math]
- Solving for Q(x) provides the lower bound.
- The geometric mean of the upper and lower bound gives a suitable approximation for [math]\displaystyle{ Q(x) }[/math]:
- [math]\displaystyle{ Q(x) \approx \frac{\phi(x)}{\sqrt{1 + x^2}}, \qquad x \geq 0. }[/math]
- Tighter bounds and approximations of [math]\displaystyle{ Q(x) }[/math] can also be obtained by optimizing the following expression [7]
- [math]\displaystyle{ \tilde{Q}(x) = \frac{\phi(x)}{(1-a)x + a\sqrt{x^2 + b}}. }[/math]
- For [math]\displaystyle{ x \geq 0 }[/math], the best upper bound is given by [math]\displaystyle{ a = 0.344 }[/math] and [math]\displaystyle{ b = 5.334 }[/math] with maximum absolute relative error of 0.44%. Likewise, the best approximation is given by [math]\displaystyle{ a = 0.339 }[/math] and [math]\displaystyle{ b = 5.510 }[/math] with maximum absolute relative error of 0.27%. Finally, the best lower bound is given by [math]\displaystyle{ a = 1/\pi }[/math] and [math]\displaystyle{ b = 2 \pi }[/math] with maximum absolute relative error of 1.17%.
- The Chernoff bound of the Q-function is
- [math]\displaystyle{ Q(x)\leq e^{-\frac{x^2}{2}}, \qquad x\gt 0 }[/math]
- Improved exponential bounds and a pure exponential approximation are [8]
- [math]\displaystyle{ Q(x)\leq \tfrac{1}{4}e^{-x^2}+\tfrac{1}{4}e^{-\frac{x^2}{2}} \leq \tfrac{1}{2}e^{-\frac{x^2}{2}}, \qquad x\gt 0 }[/math]
- [math]\displaystyle{ Q(x)\approx \frac{1}{12}e^{-\frac{x^2}{2}}+\frac{1}{4}e^{-\frac{2}{3} x^2}, \qquad x\gt 0 }[/math]
- The above were generalized by Tanash & Riihonen (2020),[9] who showed that [math]\displaystyle{ Q(x) }[/math] can be accurately approximated or bounded by
- [math]\displaystyle{ \tilde{Q}(x) = \sum_{n=1}^N a_n e^{-b_n x^2}. }[/math]
- In particular, they presented a systematic methodology to solve the numerical coefficients [math]\displaystyle{ \{(a_n,b_n)\}_{n=1}^N }[/math] that yield a minimax approximation or bound: [math]\displaystyle{ Q(x) \approx \tilde{Q}(x) }[/math], [math]\displaystyle{ Q(x) \leq \tilde{Q}(x) }[/math], or [math]\displaystyle{ Q(x) \geq \tilde{Q}(x) }[/math] for [math]\displaystyle{ x\geq0 }[/math]. With the example coefficients tabulated in the paper for [math]\displaystyle{ N = 20 }[/math], the relative and absolute approximation errors are less than [math]\displaystyle{ 2.831 \cdot 10^{-6} }[/math] and [math]\displaystyle{ 1.416 \cdot 10^{-6} }[/math], respectively. The coefficients [math]\displaystyle{ \{(a_n,b_n)\}_{n=1}^N }[/math] for many variations of the exponential approximations and bounds up to [math]\displaystyle{ N = 25 }[/math] have been released to open access as a comprehensive dataset.[10]
- Another approximation of [math]\displaystyle{ Q(x) }[/math] for [math]\displaystyle{ x \in [0,\infty) }[/math] is given by Karagiannidis & Lioumpas (2007)[11] who showed for the appropriate choice of parameters [math]\displaystyle{ \{A, B\} }[/math] that
- [math]\displaystyle{ f(x; A, B) = \frac{\left(1 - e^{-Ax}\right)e^{-x^2}}{B\sqrt{\pi} x} \approx \operatorname{erfc} \left(x\right). }[/math]
- The absolute error between [math]\displaystyle{ f(x; A, B) }[/math] and [math]\displaystyle{ \operatorname{erfc}(x) }[/math] over the range [math]\displaystyle{ [0, R] }[/math] is minimized by evaluating
- [math]\displaystyle{ \{A, B\} = \underset{\{A,B\}}{\arg \min} \frac{1}{R} \int_0^R | f(x; A, B) - \operatorname{erfc}(x) |dx. }[/math]
- Using [math]\displaystyle{ R = 20 }[/math] and numerically integrating, they found the minimum error occurred when [math]\displaystyle{ \{A, B\} = \{1.98, 1.135\}, }[/math] which gave a good approximation for [math]\displaystyle{ \forall x \ge 0. }[/math]
- Substituting these values and using the relationship between [math]\displaystyle{ Q(x) }[/math] and [math]\displaystyle{ \operatorname{erfc}(x) }[/math] from above gives
- [math]\displaystyle{ Q(x)\approx\frac{\left( 1-e^{\frac{-1.98x} {\sqrt{2}}}\right) e^{-\frac{x^{2}}{2}}}{1.135\sqrt{2\pi}x}, x \ge 0. }[/math]
- Alternative coefficients are also available for the above 'Karagiannidis–Lioumpas approximation' for tailoring accuracy for a specific application or transforming it into a tight bound.[12]
- A tighter and more tractable approximation of [math]\displaystyle{ Q(x) }[/math] for positive arguments [math]\displaystyle{ x \in [0,\infty) }[/math] is given by López-Benítez & Casadevall (2011)[13] based on a second-order exponential function:
- [math]\displaystyle{ Q(x) \approx e^{-ax^2-bx-c}, \qquad x \ge 0. }[/math]
- The fitting coefficients [math]\displaystyle{ (a,b,c) }[/math] can be optimized over any desired range of arguments in order to minimize the sum of square errors ([math]\displaystyle{ a = 0.3842 }[/math], [math]\displaystyle{ b = 0.7640 }[/math], [math]\displaystyle{ c = 0.6964 }[/math] for [math]\displaystyle{ x \in [0,20] }[/math]) or minimize the maximum absolute error ([math]\displaystyle{ a = 0.4920 }[/math], [math]\displaystyle{ b = 0.2887 }[/math], [math]\displaystyle{ c = 1.1893 }[/math] for [math]\displaystyle{ x \in [0,20] }[/math]). This approximation offers some benefits such as a good trade-off between accuracy and analytical tractability (for example, the extension to any arbitrary power of [math]\displaystyle{ Q(x) }[/math] is trivial and does not alter the algebraic form of the approximation).
Inverse Q
The inverse Q-function can be related to the inverse error functions:
- [math]\displaystyle{ Q^{-1}(y) = \sqrt{2}\ \mathrm{erf}^{-1}(1-2y) = \sqrt{2}\ \mathrm{erfc}^{-1}(2y) }[/math]
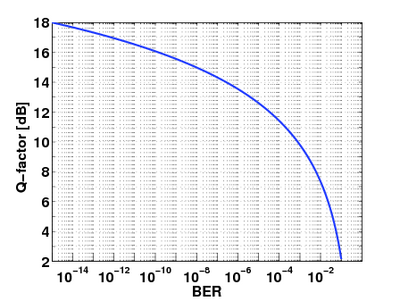
The function [math]\displaystyle{ Q^{-1}(y) }[/math] finds application in digital communications. It is usually expressed in dB and generally called Q-factor:
- [math]\displaystyle{ \mathrm{Q\text{-}factor} = 20 \log_{10}\!\left(Q^{-1}(y)\right)\!~\mathrm{dB} }[/math]
where y is the bit-error rate (BER) of the digitally modulated signal under analysis. For instance, for QPSK in additive white Gaussian noise, the Q-factor defined above coincides with the value in dB of the signal to noise ratio that yields a bit error rate equal to y.
Values
The Q-function is well tabulated and can be computed directly in most of the mathematical software packages such as R and those available in Python, MATLAB and Mathematica. Some values of the Q-function are given below for reference.
|
|
|
|
Generalization to high dimensions
The Q-function can be generalized to higher dimensions:[14]
- [math]\displaystyle{ Q(\mathbf{x})= \mathbb{P}(\mathbf{X}\geq \mathbf{x}), }[/math]
where [math]\displaystyle{ \mathbf{X}\sim \mathcal{N}(\mathbf{0},\, \Sigma) }[/math] follows the multivariate normal distribution with covariance [math]\displaystyle{ \Sigma }[/math] and the threshold is of the form [math]\displaystyle{ \mathbf{x}=\gamma\Sigma\mathbf{l}^* }[/math] for some positive vector [math]\displaystyle{ \mathbf{l}^*\gt \mathbf{0} }[/math] and positive constant [math]\displaystyle{ \gamma\gt 0 }[/math]. As in the one dimensional case, there is no simple analytical formula for the Q-function. Nevertheless, the Q-function can be approximated arbitrarily well as [math]\displaystyle{ \gamma }[/math] becomes larger and larger.[15][16]
References
- ↑ The Q-function, from cnx.org
- ↑ 2.0 2.1 Basic properties of the Q-function
- ↑ Normal Distribution Function – from Wolfram MathWorld
- ↑ Craig, J.W. (1991). "A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations". MILCOM 91 - Conference record. pp. 571–575. doi:10.1109/MILCOM.1991.258319. ISBN 0-87942-691-8. http://wsl.stanford.edu/~ee359/craig.pdf.
- ↑ Behnad, Aydin (2020). "A Novel Extension to Craig's Q-Function Formula and Its Application in Dual-Branch EGC Performance Analysis". IEEE Transactions on Communications 68 (7): 4117–4125. doi:10.1109/TCOMM.2020.2986209.
- ↑ Gordon, R.D. (1941). "Values of Mills’ ratio of area to bounding ordinate and of the normal probability integral for large values of the argument". Ann. Math. Stat. 12: 364-366.
- ↑ 7.0 7.1 Borjesson, P.; Sundberg, C.-E. (1979). "Simple Approximations of the Error Function Q(x) for Communications Applications". IEEE Transactions on Communications 27 (3): 639–643. doi:10.1109/TCOM.1979.1094433.
- ↑ Chiani, M.; Dardari, D.; Simon, M.K. (2003). "New exponential bounds and approximations for the computation of error probability in fading channels". IEEE Transactions on Wireless Communications 24 (5): 840–845. doi:10.1109/TWC.2003.814350. http://campus.unibo.it/85943/1/mcddmsTranWIR2003.pdf.
- ↑ Tanash, I.M.; Riihonen, T. (2020). "Global minimax approximations and bounds for the Gaussian Q-function by sums of exponentials". IEEE Transactions on Communications 68 (10): 6514–6524. doi:10.1109/TCOMM.2020.3006902.
- ↑ Tanash, I.M.; Riihonen, T. (2020). Coefficients for Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials [Data set]. doi:10.5281/zenodo.4112978. https://zenodo.org/record/4112978.
- ↑ Karagiannidis, George; Lioumpas, Athanasios (2007). "An Improved Approximation for the Gaussian Q-Function". IEEE Communications Letters 11 (8): 644–646. doi:10.1109/LCOMM.2007.070470. http://users.auth.gr/users/9/3/028239/public_html/pdf/Q_Approxim.pdf.
- ↑ Tanash, I.M.; Riihonen, T. (2021). "Improved coefficients for the Karagiannidis–Lioumpas approximations and bounds to the Gaussian Q-function". IEEE Communications Letters 25 (5): 1468–1471. doi:10.1109/LCOMM.2021.3052257.
- ↑ Lopez-Benitez, Miguel; Casadevall, Fernando (2011). "Versatile, Accurate, and Analytically Tractable Approximation for the Gaussian Q-Function". IEEE Transactions on Communications 59 (4): 917–922. doi:10.1109/TCOMM.2011.012711.100105. http://www.lopezbenitez.es/journals/IEEE_TCOM_2011.pdf.
- ↑ Savage, I. R. (1962). "Mills ratio for multivariate normal distributions". Journal of Research of the National Bureau of Standards Section B 66 (3): 93–96. doi:10.6028/jres.066B.011.
- ↑ Botev, Z. I. (2016). "The normal law under linear restrictions: simulation and estimation via minimax tilting". Journal of the Royal Statistical Society, Series B 79: 125–148. doi:10.1111/rssb.12162. Bibcode: 2016arXiv160304166B.
- ↑ Botev, Z. I.; Mackinlay, D.; Chen, Y.-L. (2017). "Logarithmically efficient estimation of the tail of the multivariate normal distribution". 2017 Winter Simulation Conference (WSC). IEEE. pp. 1903–191. doi:10.1109/WSC.2017.8247926. ISBN 978-1-5386-3428-8.
 |  |
