Radial basis function interpolation

Radial basis function (RBF) interpolation is an advanced method in approximation theory for constructing high-order accurate interpolants of unstructured data, possibly in high-dimensional spaces. The interpolant takes the form of a weighted sum of radial basis functions. RBF interpolation is a mesh-free method, meaning the nodes (points in the domain) need not lie on a structured grid, and does not require the formation of a mesh. It is often spectrally accurate and stable for large numbers of nodes even in high dimensions. Many interpolation methods can be used as the theoretical foundation of algorithms for approximating linear operators, and RBF interpolation is no exception. RBF interpolation has been used to approximate differential operators, integral operators, and surface differential operators.

Examples

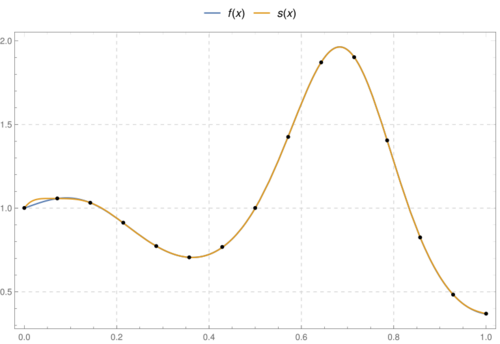
Let [math]\displaystyle{ f(x) = \exp(x \cos(3 \pi x)) }[/math] and let [math]\displaystyle{ x_k = \frac{k}{14}, k=0, 1, \dots, 14 }[/math] be 15 equally spaced points on the interval [math]\displaystyle{ [0, 1] }[/math]. We will form [math]\displaystyle{ s(x) = \sum\limits_{k=0}^{14} w_k \varphi(\|x-x_k\|) }[/math] where [math]\displaystyle{ \varphi }[/math] is a radial basis function, and choose [math]\displaystyle{ w_k, k=0, 1, \dots, 14 }[/math] such that [math]\displaystyle{ s(x_k)=f(x_k), k=0, 1, \dots, 14 }[/math] ([math]\displaystyle{ s }[/math] interpolates [math]\displaystyle{ f }[/math] at the chosen points). In matrix notation this can be written as

[math]\displaystyle{ \begin{bmatrix} \varphi(\|x_0 - x_0\|) & \varphi(\|x_1 - x_0\|) & \dots & \varphi(\|x_{14} - x_0\|) \\ \varphi(\|x_0 - x_1\|) & \varphi(\|x_1 - x_1\|) & \dots & \varphi(\|x_{14} - x_{1}\|) \\ \vdots & \vdots & \ddots & \vdots \\ \varphi(\|x_0 - x_{14}\|) & \varphi(\|x_1 - x_{14}\|) & \dots & \varphi(\|x_{14} - x_{14}\|) \\ \end{bmatrix} \begin{bmatrix}w_0 \\ w_1 \\ \vdots \\ w_{14}\end{bmatrix} = \begin{bmatrix}f(x_0) \\ f(x_1) \\ \vdots \\ f(x_{14})\end{bmatrix}. }[/math]

Choosing [math]\displaystyle{ \varphi(r) = \exp(-(\varepsilon r)^2) }[/math], the Gaussian, with a shape parameter of [math]\displaystyle{ \varepsilon = 3 }[/math], we can then solve the matrix equation for the weights and plot the interpolant. Plotting the interpolating function below, we see that it is visually the same everywhere except near the left boundary (an example of Runge's phenomenon), where it is still a very close approximation. More precisely the maximum error is roughly [math]\displaystyle{ \|f - s\|_\infty \approx 0.0267414 }[/math] at [math]\displaystyle{ x = 0.0220012 }[/math].

The function [math]\displaystyle{ f(x) = \exp(x \cos(3 \pi x)) }[/math] sampled at 15 uniform nodes between 0 and 1, interpolated using the Gaussian RBF with a shape parameter of [math]\displaystyle{ \varepsilon = 3 }[/math].

The interpolation error, [math]\displaystyle{ s(x) - f(x) }[/math], for the plot to the left.

Motivation

The Mairhuber–Curtis theorem says that for any open set [math]\displaystyle{ V }[/math] in [math]\displaystyle{ \mathbb{R}^n }[/math] with [math]\displaystyle{ n \geq 2 }[/math], and [math]\displaystyle{ f_1, f_2, \dots, f_n }[/math] linearly independent functions on [math]\displaystyle{ V }[/math], there exists a set of [math]\displaystyle{ n }[/math] points in the domain such that the interpolation matrix

[math]\displaystyle{ \begin{bmatrix} f_1(x_1) & f_2(x_1) & \dots & f_n(x_1) \\ f_1(x_2) & f_2(x_2) & \dots & f_n(x_2) \\ \vdots & \vdots & \ddots & \vdots \\ f_1(x_n) & f_2(x_n) & \dots & f_n(x_n) \end{bmatrix} }[/math]

is singular.

This means that if one wishes to have a general interpolation algorithm, one must choose the basis functions to depend on the interpolation points. In 1971, Rolland Hardy developed a method of interpolating scattered data using interpolants of the form [math]\displaystyle{ s(\mathbf{x}) = \sum\limits_{k=1}^N \sqrt{\|\mathbf{x} - \mathbf{x}_k\|^2 + C} }[/math]. This is interpolation using a basis of shifted multiquadric functions, now more commonly written as [math]\displaystyle{ \varphi(r) = \sqrt{1+(\varepsilon r)^2} }[/math], and is the first instance of radial basis function interpolation. It has been shown that the resulting interpolation matrix will always be non-singular. This does not violate the Mairhuber–Curtis theorem since the basis functions depend on the points of interpolation. Choosing a radial kernel such that the interpolation matrix is non-singular is exactly the definition of a strictly positive definite function. Such functions, including the Gaussian, inverse quadratic, and inverse multiquadric are often used as radial basis functions for this reason.

Shape-parameter tuning

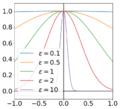
Many radial basis functions have a parameter that controls their relative flatness or peakedness. This parameter is usually represented by the symbol [math]\displaystyle{ \varepsilon }[/math] with the function becoming increasingly flat as [math]\displaystyle{ \varepsilon \to 0 }[/math]. For example, Rolland Hardy used the formula [math]\displaystyle{ \varphi(r) = \sqrt{r^2 + C} }[/math] for the multiquadric, however nowadays the formula [math]\displaystyle{ \varphi(r) = \sqrt{1 + (\varepsilon r)^2} }[/math] is used instead. These formulas are equivalent up to a scale factor. This factor is inconsequential since the basis vectors have the same span and the interpolation weights will compensate. By convention, the basis function is scaled such that [math]\displaystyle{ \varphi(0) = 1 }[/math] as seen in the plots of the Gaussian functions and the bump functions.

• 

  A Gaussian function for several choices of [math]\displaystyle{ \varepsilon }[/math]

• 

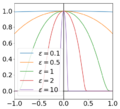
  A plot of the scaled bump function with several choices of shape parameter

An RBF interpolant of the function f(x)=e^(x*cos(3*pi*x))-1 sampled at 15 points, using Gaussians, with a very large shape parameter e=100. The "bed-of-nails interpolant."

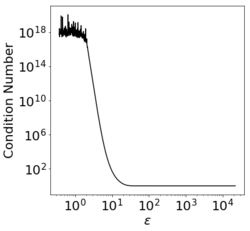
A consequence of this choice, is that the interpolation matrix approaches the identity matrix as [math]\displaystyle{ \varepsilon \to \infty }[/math] leading to stability when solving the matrix system. The resulting interpolant will in general be a poor approximation to the function since it will be near zero everywhere, except near the interpolation points where it will sharply peak – the so-called "bed-of-nails interpolant" (as seen in the plot to the right).

A plot of the condition number by the shape parameter for a 15x15 radial basis function interpolation matrix using the Gaussian

On the opposite side of the spectrum, the condition number of the interpolation matrix will diverge to infinity as [math]\displaystyle{ \varepsilon \to 0 }[/math] leading to ill-conditioning of the system. In practice, one chooses a shape parameter so that the interpolation matrix is "on the edge of ill-conditioning" (eg. with a condition number of roughly [math]\displaystyle{ 10^{12} }[/math] for double-precision floating point).

There are sometimes other factors to consider when choosing a shape-parameter. For example the bump function [math]\displaystyle{ \varphi(r) = \begin{cases} \exp\left( -\frac{1}{1 - (\varepsilon r)^2}\right) & \mbox{ for } r\lt \frac{1}{\varepsilon} \\ 0 & \mbox{ otherwise} \end{cases} }[/math] has a compact support (it is zero everywhere except when [math]\displaystyle{ r\lt \tfrac{1}{\varepsilon} }[/math]) leading to a sparse interpolation matrix.

Some radial basis functions such as the polyharmonic splines have no shape-parameter.

See also

• Kriging