Rectangular mask short-time Fourier transform

In mathematics and Fourier analysis, a rectangular mask short-time Fourier transform (rec-STFT) is a simplified form of the short-time Fourier transform which is used to analyze how a signal's frequency content changes over time. In rec-STFT, a rectangular window (a simple on/off time-limiting function) is used to isolate short time segments of the signal. Other types of the STFT may require more computation time ( refers to the amount of time it takes a computer or algorithm to perform a calculation or complete a task) than the rec-STFT.

The rectangular mask function can be defined for some bound (B) over time (t) as

$w(t)=\{\begin{array}{ll}1;& |t|\le B\\ 0;& |t|>B\end{array}$

B = 50, x-axis (sec)

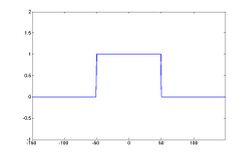
We can change B for different tradeoffs between desired time resolution and frequency resolution.

Rec-STFT

$X(t,f)=\underset{t-B}{\overset{t+B}{\int }}x(\tau )e^{-j2\pi f\tau }d\tau$

Inverse form

$x(t)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}X(t_1,f)e^{j2\pi ft}df\text{ where }t-B<t_1<t+B$

Property

Rec-STFT has similar properties with Fourier transform

• Integration

(a)

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}X(t,f)df=\underset{t-B}{\overset{t+B}{\int }}x(\tau )\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{e}^{-j2\pi f\tau }dfd\tau =\underset{t-B}{\overset{t+B}{\int }}x(\tau )\delta (\tau )d\tau =\{\begin{array}{ll}x(0);& |t|<B\\ 0;& \text{otherwise}\end{array}$

(b)

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}X(t,f)e^{-j2\pi fv}df=\{\begin{array}{ll}x(v);& v-B<t<v+B\\ 0;& \text{otherwise}\end{array}$

• Shifting property (shift along x-axis)

$\underset{t-B}{\overset{t+B}{\int }}x(\tau +{\tau }_0)e^{-j2\pi f\tau }d\tau =X(t+{\tau }_0,f)e^{j2\pi f{\tau }_0}$

• Modulation property (shift along y-axis)

$\underset{t-B}{\overset{t+B}{\int }}[x(\tau )e^{j2\pi f_0\tau }]d\tau =X(t,f-f_0)$

• special input

1. When $x(t)=\delta (t),X(t,f)=\{\begin{array}{ll}1;& |t|<B\\ 0;& \text{otherwise}\end{array}$
2. When $x(t)=1,X(t,f)=2B\mathrm{sinc}(2Bf)e^{j2\pi ft}$

• Linearity property

If $h(t)=\alpha x(t)+\beta y(t)$,$H(t,f),X(t,f),$and $Y(t,f)$are their rec-STFTs, then

$H(t,f)=\alpha X(t,f)+\beta Y(t,f).$

• Power integration property

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}|X(t,f){|}^{2}df=\underset{t-B}{\overset{t+B}{\int }}|x(\tau ){|}^{2}d\tau$

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}|X(t,f){|}^{2}dfdt=2B\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}|x(\tau ){|}^{2}d\tau$

• Energy sum property (Parseval's theorem)

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}X(t,f)Y^{*}(t,f)df=\underset{t-B}{\overset{t+B}{\int }}x(\tau )y^{*}(\tau )d\tau$

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}X(t,f)Y^{*}(t,f)dfdt=2B\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x(\tau )y^{*}(\tau )d\tau$

Example of tradeoff with different B

Spectrograms produced from applying a rec-STFT on a function consisting of 3 consecutive cosine waves. (top spectrogram uses smaller B of 0.5, middle uses B of 1, and bottom uses larger B of 2.)

From the image, when B is smaller, the time resolution is better. Otherwise, when B is larger, the frequency resolution is better.

Advantage and disadvantage

Compared with the Fourier transform:

• Advantage: The instantaneous frequency can be observed.
• Disadvantage: Higher complexity of computation.

Compared with other types of time-frequency analysis:

• Advantage: Least computation time for digital implementation.
• Disadvantage: Quality is worse than other types of time-frequency analysis. The jump discontinuity of the edges of the rectangular mask results in Gibbs ringing artifacts in the frequency domain, which can be alleviated with smoother windows.

See also

• Uncertainty principle

References

1. Jian-Jiun Ding (2014) Time-frequency analysis and wavelet transform