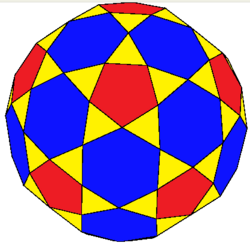
Rectified truncated icosahedron
| Rectified truncated icosahedron | |
|---|---|
 | |
| Type | Near-miss Johnson solid |
| Faces | 92: 60 isosceles triangles 12 pentagons 20 hexagons |
| Edges | 180 |
| Vertices | 90 |
| Vertex configuration | 3.6.3.6  3.5.3.6  |
| Schläfli symbol | rt{3,5} |
| Symmetry group | Ih, [5,3], (*532) order 120 |
| Rotation group | I, [5,3]+, (532), order 60 |
| Dual polyhedron | Rhombic enneacontahedron |
| Properties | convex |
| Net | |
 | |
In geometry, the rectified truncated icosahedron is a convex polyhedron. It has 92 faces: 60 isosceles triangles, 12 regular pentagons, and 20 regular hexagons. It is constructed as a rectified, truncated icosahedron, rectification truncating vertices down to mid-edges.
As a near-miss Johnson solid, under icosahedral symmetry, the pentagons are always regular, although the hexagons, while having equal edge lengths, do not have the same edge lengths with the pentagons, having slightly different but alternating angles, causing the triangles to be isosceles instead. The shape is a symmetrohedron with notation I(1,2,*,[2])
Images
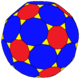
Dual
By Conway polyhedron notation, the dual polyhedron can be called a joined truncated icosahedron, jtI, but it is topologically equivalent to the rhombic enneacontahedron with all rhombic faces.
Related polyhedra
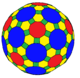
The rectified truncated icosahedron can be seen in sequence of rectification and truncation operations from the truncated icosahedron. Further truncation, and alternation operations creates two more polyhedra:
| Name | Truncated icosahedron |
Truncated truncated icosahedron |
Rectified truncated icosahedron |
Expanded truncated icosahedron |
Truncated rectified truncated icosahedron |
Snub rectified truncated icosahedron |
|---|---|---|---|---|---|---|
| Coxeter | tI | ttI | rtI | rrtI | trtI | srtI |
| Conway | atI | etI | btI | stI | ||
| Image | 
|
|

|

|
|

|
| Net | 
|

|
|
|

| |
| Conway | dtI = kD kD | kdtI | jtI jtI | otI | mtI | gtI |
| Dual | 
|

|

|

|

|
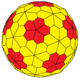
|
| Net | 
|

|

|
|

|
See also
- Near-miss Johnson solid
- Rectified truncated tetrahedron
- Rectified truncated octahedron
- Rectified truncated cube
- Rectified truncated dodecahedron
References
- Coxeter Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (pp. 145–154 Chapter 8: Truncation)
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
External links
- George Hart's Conway interpreter: generates polyhedra in VRML, taking Conway notation as input
 |


