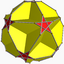
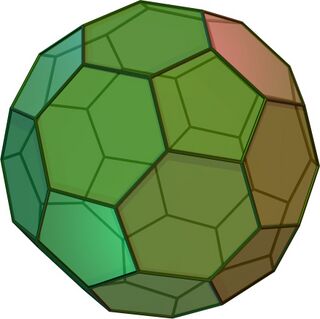
Truncated icosahedron

Short description: Archimedean solid

Truncated icosahedron
(Click here for rotating model)
Type	Archimedean solid Uniform polyhedron
Elements	F = 32, E = 90, V = 60 (χ = 2)
Faces by sides	12{5}+20{6}
Conway notation	tI
Schläfli symbols	t{3,5}
	t0,1{3,5}
Wythoff symbol	2 5 | 3
Coxeter diagram
Symmetry group	Ih, H3, [5,3], (*532), order 120
Rotation group	I, [5,3]+, (532), order 60
Dihedral angle	6-6: 138.189685° 6-5: 142.62°
References	U25, C27, W9
Properties	Semiregular convex
Colored faces	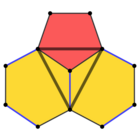5.6.6 (Vertex figure)
Pentakis dodecahedron (dual polyhedron)	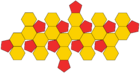Net

In geometry, the truncated icosahedron is an Archimedean solid, one of 13 convex isogonal nonprismatic solids whose 32 faces are two or more types of regular polygons. It is the only one of these shapes that does not contain triangles or squares. In general usage, the degree of truncation is assumed to be uniform unless specified.

It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.

It is the Goldberg polyhedron GP_V(1,1) or {5+,3}_1,1, containing pentagonal and hexagonal faces.

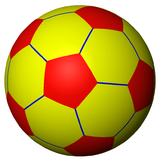
This geometry is associated with footballs (soccer balls) typically patterned with white hexagons and black pentagons. Geodesic domes such as those whose architecture Buckminster Fuller pioneered are often based on this structure. It also corresponds to the geometry of the fullerene C₆₀ ("buckyball") molecule.

It is used in the cell-transitive hyperbolic space-filling tessellation, the bitruncated order-5 dodecahedral honeycomb.

Construction

Icosahedron

This polyhedron can be constructed from an icosahedron by truncating, or cutting off, each of the 12 vertices at the one-third mark of each edge, creating 12 pentagonal faces and transforming the original 20 triangle faces into regular hexagons.

Characteristics

In geometry and graph theory, there are some standard polyhedron characteristics.

Cartesian coordinates

Cartesian coordinates for the vertices of a truncated icosahedron centered at the origin are all even permutations of: [math]\displaystyle{ \begin{alignat}{5} \Bigl( && 0,&& \pm\,1,&& \pm\,3\varphi \Bigr), \\[2pt] \Bigl( && \pm\,1,&& \quad \pm\,(2 + \varphi),&& \pm\,2\varphi \Bigr), \\[2pt] \Bigl( && \pm\,\varphi,&& \pm\,2,&& \quad \pm\,(2\varphi + 1) \Bigr), \end{alignat} }[/math]

where [math]\displaystyle{ \varphi = \tfrac{1 + \sqrt 5}{2} }[/math] is the golden mean. The circumradius is [math]\displaystyle{ \sqrt{9\varphi + 10} \approx 4.956 }[/math] and the edges have length 2.

Orthogonal projections

The truncated icosahedron has five special orthogonal projections, centered, on a vertex, on two types of edges, and two types of faces: hexagonal and pentagonal. The last two correspond to the A₂ and H₂ Coxeter planes.

Orthogonal projections

Centered by	Vertex	Edge 5-6	Edge 6-6	Face Hexagon	Face Pentagon
Solid
Wireframe
Projective symmetry	[2]	[2]	[2]	[6]	[10]
Dual

Spherical tiling

The truncated icosahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

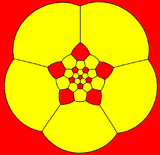	pentagon-centered	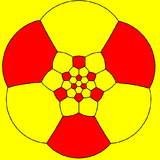hexagon-centered
Orthographic projection	Stereographic projections

Dimensions

Mutually orthogonal golden rectangles drawn into the original icosahedron (before cut off)

If the edge length of a truncated icosahedron is a, the radius of a circumscribed sphere (one that touches the truncated icosahedron at all vertices) is: [math]\displaystyle{ r_\mathrm{u} = \frac{a}{2} \sqrt{1 + 9\varphi^2} = \frac{a}{4} \sqrt{58 +18\sqrt{5}} \approx 2.478\,018\,66 a }[/math]

where φ is the golden ratio.

This result is easy to get by using one of the three orthogonal golden rectangles drawn into the original icosahedron (before cut off) as the starting point for our considerations. The angle between the segments joining the center and the vertices connected by shared edge (calculated on the basis of this construction) is approximately 23.281446°.

Area and volume

The area A and the volume V of the truncated icosahedron of edge length a are: [math]\displaystyle{ \begin{align} A & = \left ( 20 \cdot \frac32\sqrt{3} + 12 \cdot \frac54\sqrt{ 1 + \frac{2}{\sqrt{5}}} \right ) a^2 &&\approx 72.607\,253a^2 \\ V & = \frac{125+43\sqrt{5}}{4} a^3 &&\approx 55.287\,7308a^3. \end{align} }[/math] With unit edges, the surface area is (rounded) 21 for the pentagons and 52 for the hexagons, together 73 (see areas of regular polygons). The truncated icosahedron easily demonstrates the Euler characteristic: [math]\displaystyle{ \chi = \underset{(32)}{F} + \underset{(60)}{V} - \underset{(90)}{E} = 2. }[/math]

Applications

The balls used in association football and team handball are perhaps the best-known example of a spherical polyhedron analog to the truncated icosahedron, found in everyday life. The ball comprises the same pattern of regular pentagons and regular hexagons, but it is more spherical due to the pressure of the air inside and the elasticity of the ball. This ball type was introduced to the World Cup in 1970 (starting in 2006, this iconic design has been superseded by alternative patterns).

British traffic signs indicating football grounds use a uniformly-colored hexagonal tiling section to represent a football, rather than a truncated icosahedron. Mathematician and comedian Matt Parker started a petition to the UK government to have these signs changed to be geometrically accurate. The petition was ultimately declined.

Geodesic domes are typically based on triangular facetings of this geometry with example structures found across the world, popularized by Buckminster Fuller.

A variation of the icosahedron was used as the basis of the honeycomb wheels (made from a polycast material) used by the Pontiac Motor Division between 1971 and 1976 on its Trans Am and Grand Prix.

This shape was also the configuration of the lenses used for focusing the explosive shock waves of the detonators in both the gadget and Fat Man atomic bombs.

The truncated icosahedron can also be described as a model of the Buckminsterfullerene (fullerene) (C₆₀), or "buckyball", molecule – an allotrope of elemental carbon, discovered in 1985. The diameter of the football and the fullerene molecule are 22 cm and about 0.71 nm, respectively, hence the size ratio is ≈31,000,000:1.

In popular craft culture, large sparkleballs can be made using a icosahedron pattern and plastic, styrofoam or paper cups.

In the arts

• Gallery
• 

  The truncated icosahedron (left) compared with an association football.

• 

  Fullerene C₆₀ molecule

• 

  Truncated icosahedral radome on a weather station

• 

  Truncated icosahedron machined out of 6061-T6 aluminum

• 

  A wooden truncated icosahedron artwork by George W. Hart.

Related polyhedra

These uniform star-polyhedra, and one icosahedral stellation have nonuniform truncated icosahedra convex hulls:

Uniform star polyhedra with truncated icosahedra convex hulls
Nonuniform truncated icosahedron 2 5 | 3 U37 2 5/2 | 5 U61 5/2 3 | 5/3 U67 5/3 3 | 2 U73 2 5/3 (3/2 5/4) Complete stellation Nonuniform truncated icosahedron 2 5 | 3 U38 5/2 5 | 2 U44 5/3 5 | 3 U56 2 3 (5/4 5/2) | Nonuniform truncated icosahedron 2 5 | 3 U32 | 5/2 3 3

This polyhedron looks similar to the uniform chamfered dodecahedron which has 12 pentagons, but 30 hexagons.

Truncated icosahedral graph

Truncated icosahedral graph
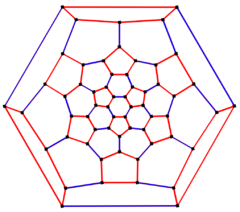6-fold symmetry schlegel diagram
Vertices	60
Edges	90
Automorphisms	120
Chromatic number	3
Properties	Cubic, Hamiltonian, regular, zero-symmetric
Table of graphs and parameters

In the mathematical field of graph theory, a truncated icosahedral graph is the graph of vertices and edges of the truncated icosahedron, one of the Archimedean solids. It has 60 vertices and 90 edges, and is a cubic Archimedean graph.

Orthographic projection

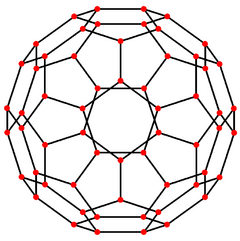5-fold symmetry

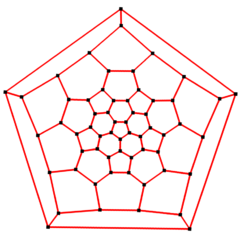5-fold Schlegel diagram

History

Piero della Francesca's image of a truncated icosahedron from his book De quinque corporibus regularibus

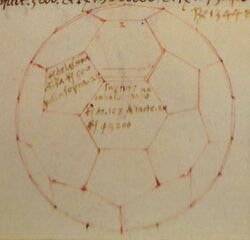
The truncated icosahedron was known to Archimedes, who classified the 13 Archimedean solids in a lost work. All we know of his work on these shapes comes from Pappus of Alexandria, who merely lists the numbers of faces for each: 12 pentagons and 20 hexagons, in the case of the truncated icosahedron. The first known image and complete description of a truncated icosahedron is from a rediscovery by Piero della Francesca, in his 15th-century book De quinque corporibus regularibus, which included five of the Archimedean solids (the five truncations of the regular polyhedra). The same shape was depicted by Leonardo da Vinci, in his illustrations for Luca Pacioli's plagiarism of della Francesca's book in 1509. Although Albrecht Dürer omitted this shape from the other Archimedean solids listed in his 1525 book on polyhedra, Underweysung der Messung, a description of it was found in his posthumous papers, published in 1538. Johannes Kepler later rediscovered the complete list of the 13 Archimedean solids, including the truncated icosahedron, and included them in his 1609 book, Harmonices Mundi.

See also

• Fullerene
  • Buckminsterfullerene (C₆₀)
• Hyperbolic soccerball
• Snyder equal-area projection
• Soccer ball
  • Adidas Telstar

References

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.  (Section 3-9)
• Cromwell, P. (1997). "Archimedean solids". Polyhedra: "One of the Most Charming Chapters of Geometry". Cambridge: Cambridge University Press. pp. 79–86. ISBN 0-521-55432-2. OCLC 180091468. 

External links

• Eric W. Weisstein, Truncated icosahedron (Archimedean solid) at MathWorld.
  • Weisstein, Eric W.. "Truncated icosahedral graph". http://mathworld.wolfram.com/TruncatedIcosahedralGraph.html. 
• Klitzing, Richard. "3D convex uniform polyhedra x3x5o - ti". https://bendwavy.org/klitzing/dimensions/polyhedra.htm. 
• Editable printable net of a truncated icosahedron with interactive 3D view
• The Uniform Polyhedra
• "Virtual Reality Polyhedra"—The Encyclopedia of Polyhedra
• 3D paper data visualization World Cup ball