Zero-symmetric graph

The smallest zero-symmetric graph, with 18 vertices and 27 edges

The truncated cuboctahedron, a zero-symmetric polyhedron

Graph families defined by their automorphisms
distance-transitive	→	distance-regular	←	strongly regular
↓
symmetric (arc-transitive)	←	t-transitive, t ≥ 2		skew-symmetric
↓
(if connected) vertex- and edge-transitive	→	edge-transitive and regular	→	edge-transitive
↓		↓		↓
vertex-transitive	→	regular	→	(if bipartite) biregular
↑
Cayley graph	←	zero-symmetric		asymmetric

In the mathematical field of graph theory, a zero-symmetric graph is a connected graph in which each vertex has exactly three incident edges and, for each two vertices, there is a unique symmetry taking one vertex to the other. Such a graph is a vertex-transitive graph but cannot be an edge-transitive graph: the number of symmetries equals the number of vertices, too few to take every edge to every other edge.

The smallest zero-symmetric graph with two edge orbits

The name for this class of graphs was coined by R. M. Foster in a 1966 letter to H. S. M. Coxeter. In the context of group theory, zero-symmetric graphs are also called graphical regular representations of their symmetry groups.

Examples

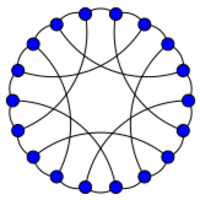
The smallest zero-symmetric graph is a nonplanar graph with 18 vertices. Its LCF notation is [5,−5]⁹.

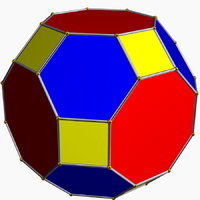
Among planar graphs, the truncated cuboctahedral and truncated icosidodecahedral graphs are also zero-symmetric.

These examples are all bipartite graphs. However, there exist larger examples of zero-symmetric graphs that are not bipartite.

These examples also have three different symmetry classes (orbits) of edges. However, there exist zero-symmetric graphs with only two orbits of edges. The smallest such graph has 20 vertices, with LCF notation [6,6,-6,-6]⁵.

Properties

Every finite zero-symmetric graph is a Cayley graph, a property that does not always hold for cubic vertex-transitive graphs more generally and that helps in the solution of combinatorial enumeration tasks concerning zero-symmetric graphs. There are 97687 zero-symmetric graphs on up to 1280 vertices. These graphs form 89% of the cubic Cayley graphs and 88% of all connected vertex-transitive cubic graphs on the same number of vertices.

Unsolved problem in mathematics: Does every finite zero-symmetric graph contain a Hamiltonian cycle? (more unsolved problems in mathematics)

All known finite connected zero-symmetric graphs contain a Hamiltonian cycle, but it is unknown whether every finite connected zero-symmetric graph is necessarily Hamiltonian. This is a special case of the Lovász conjecture that (with five known exceptions, none of which is zero-symmetric) every finite connected vertex-transitive graph and every finite Cayley graph is Hamiltonian.

See also

• Semi-symmetric graph, graphs that have symmetries between every two edges but not between every two vertices (reversing the roles of edges and vertices in the definition of zero-symmetric graphs)