Semiregular polytope

Short description: Isogonal polytope with regular facets

Gosset's figures

3D honeycombs
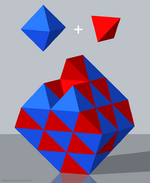Simple tetroctahedric check	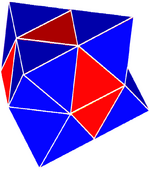Complex tetroctahedric check
4D polytopes
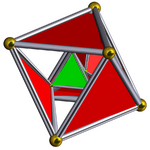Tetroctahedric	Octicosahedric	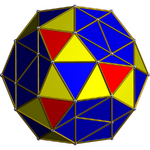Tetricosahedric

In geometry, by Thorold Gosset's definition a semiregular polytope is usually taken to be a polytope that is vertex-transitive and has all its facets being regular polytopes. E.L. Elte compiled a longer list in 1912 as The Semiregular Polytopes of the Hyperspaces which included a wider definition.

Gosset's list

In three-dimensional space and below, the terms semiregular polytope and uniform polytope have identical meanings, because all uniform polygons must be regular. However, since not all uniform polyhedra are regular, the number of semiregular polytopes in dimensions higher than three is much smaller than the number of uniform polytopes in the same number of dimensions.

The three convex semiregular 4-polytopes are the rectified 5-cell, snub 24-cell and rectified 600-cell. The only semiregular polytopes in higher dimensions are the k₂₁ polytopes, where the rectified 5-cell is the special case of k = 0. These were all listed by Gosset, but a proof of the completeness of this list was not published until the work of (Makarov 1988) for four dimensions, and (Blind Blind) for higher dimensions.

Gosset's 4-polytopes (with his names in parentheses)

Rectified 5-cell (Tetroctahedric),

Rectified 600-cell (Octicosahedric),

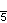
Snub 24-cell (Tetricosahedric), , or

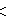
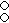
Semiregular E-polytopes in higher dimensions

5-demicube (5-ic semi-regular), a 5-polytope, ↔

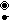
2₂₁ polytope (6-ic semi-regular), a 6-polytope, or

3₂₁ polytope (7-ic semi-regular), a 7-polytope,

4₂₁ polytope (8-ic semi-regular), an 8-polytope,

Euclidean honeycombs

The tetrahedral-octahedral honeycomb in Euclidean 3-space has alternating tetrahedral and octahedral cells.

Semiregular polytopes can be extended to semiregular honeycombs. The semiregular Euclidean honeycombs are the tetrahedral-octahedral honeycomb (3D), gyrated alternated cubic honeycomb (3D) and the 5₂₁ honeycomb (8D).

Gosset honeycombs:

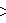
1. Tetrahedral-octahedral honeycomb or alternated cubic honeycomb (Simple tetroctahedric check), ↔ (Also quasiregular polytope)
2. Gyrated alternated cubic honeycomb (Complex tetroctahedric check),

Semiregular E-honeycomb:

• 5₂₁ honeycomb (9-ic check) (8D Euclidean honeycomb),

(Gosset 1900) additionally allowed Euclidean honeycombs as facets of higher-dimensional Euclidean honeycombs, giving the following additional figures:

1. Hypercubic honeycomb prism, named by Gosset as the (n – 1)-ic semi-check (analogous to a single rank or file of a chessboard)
2. Alternated hexagonal slab honeycomb (tetroctahedric semi-check),

Hyperbolic honeycombs

The hyperbolic tetrahedral-octahedral honeycomb has tetrahedral and two types of octahedral cells.

There are also hyperbolic uniform honeycombs composed of only regular cells (Coxeter Whitrow), including:

• Hyperbolic uniform honeycombs, 3D honeycombs:
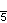
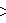
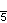
  1. Alternated order-5 cubic honeycomb, ↔ (Also quasiregular polytope)
  2. Tetrahedral-octahedral honeycomb,
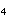
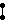
  3. Tetrahedron-icosahedron honeycomb,
• Paracompact uniform honeycombs, 3D honeycombs, which include uniform tilings as cells:
  1. Rectified order-6 tetrahedral honeycomb,
  2. Rectified square tiling honeycomb,
  3. Rectified order-4 square tiling honeycomb, ↔
  4. Alternated order-6 cubic honeycomb, ↔ (Also quasiregular)
  5. Alternated hexagonal tiling honeycomb, ↔
  6. Alternated order-4 hexagonal tiling honeycomb, ↔
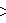
  7. Alternated order-5 hexagonal tiling honeycomb, ↔
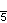
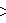
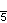
  8. Alternated order-6 hexagonal tiling honeycomb, ↔
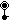
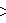
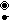
  9. Alternated square tiling honeycomb, ↔ (Also quasiregular)
  10. Cubic-square tiling honeycomb,
  11. Order-4 square tiling honeycomb, =
  12. Tetrahedral-triangular tiling honeycomb,
• 9D hyperbolic paracompact honeycomb:
  1. 6₂₁ honeycomb (10-ic check),

See also

• Semiregular polyhedron

References

• Blind, G. (1991). "The semiregular polytopes". Commentarii Mathematici Helvetici 66 (1): 150–154. doi:10.1007/BF02566640. 
• Coxeter, H. S. M. (1973). Regular Polytopes (3rd ed.). New York: Dover Publications. ISBN 0-486-61480-8. 
• "World-structure and non-Euclidean honeycombs". Proceedings of the Royal Society 201 (1066): 417–437. 1950. doi:10.1098/rspa.1950.0070. Bibcode: 1950RSPSA.201..417C. 
• Elte, E. L. (1912). The Semiregular Polytopes of the Hyperspaces. Groningen: University of Groningen. ISBN 1-4181-7968-X. 
• Gosset, Thorold (1900). "On the regular and semi-regular figures in space of n dimensions". Messenger of Mathematics 29: 43–48. 
• Makarov, P. V. (1988). "On the derivation of four-dimensional semi-regular polytopes". Mat. Issled. Akad. Nauk. Mold. 103: 139–150, 177.