5-demicube
| Demipenteract (5-demicube) | ||
|---|---|---|
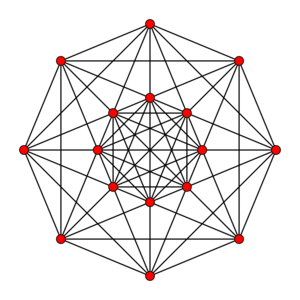 Petrie polygon projection | ||
| Type | Uniform 5-polytope | |
| Family (Dn) | 5-demicube | |
| Families (En) | k21 polytope 1k2 polytope | |
| Coxeter symbol |
121 | |
| Schläfli symbols |
{3,32,1} = h{4,33} s{2,4,3,3} or h{2}h{4,3,3} sr{2,2,4,3} or h{2}h{2}h{4,3} h{2}h{2}h{2}h{4} s{21,1,1,1} or h{2}h{2}h{2}s{2} | |
| Coxeter diagrams |
||
| 4-faces | 26 | 10 {31,1,1} 16 {3,3,3} |
| Cells | 120 | 40 {31,0,1} 80 {3,3} |
| Faces | 160 | {3} |
| Edges | 80 | |
| Vertices | 16 | |
| Vertex figure |
 rectified 5-cell | |
| Petrie polygon |
Octagon | |
| Symmetry | D5, [32,1,1] = [1+,4,33] [24]+ | |
| Properties | convex | |
In five-dimensional geometry, a demipenteract or 5-demicube is a semiregular 5-polytope, constructed from a 5-hypercube (penteract) with alternated vertices removed.
It was discovered by Thorold Gosset. Since it was the only semiregular 5-polytope (made of more than one type of regular facets), he called it a 5-ic semi-regular. E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as HM5 for a 5-dimensional half measure polytope.
Coxeter named this polytope as 121 from its Coxeter diagram, which has branches of length 2, 1 and 1 with a ringed node on one of the short branches, ![]()
![]()
![]()
![]()
![]()
![]()
![]() and Schläfli symbol [math]\displaystyle{ \left\{3 \begin{array}{l}3, 3\\3\end{array}\right\} }[/math] or {3,32,1}.
and Schläfli symbol [math]\displaystyle{ \left\{3 \begin{array}{l}3, 3\\3\end{array}\right\} }[/math] or {3,32,1}.
It exists in the k21 polytope family as 121 with the Gosset polytopes: 221, 321, and 421.
The graph formed by the vertices and edges of the demipenteract is sometimes called the Clebsch graph, though that name sometimes refers to the folded cube graph of order five instead.
Cartesian coordinates
Cartesian coordinates for the vertices of a demipenteract centered at the origin and edge length 2√2 are alternate halves of the penteract:
- (±1,±1,±1,±1,±1)
with an odd number of plus signs.
As a configuration
This configuration matrix represents the 5-demicube. The rows and columns correspond to vertices, edges, faces, cells and 4-faces. The diagonal numbers say how many of each element occur in the whole 5-demicube. The nondiagonal numbers say how many of the column's element occur in or at the row's element.[1][2]
The diagonal f-vector numbers are derived through the Wythoff construction, dividing the full group order of a subgroup order by removing one mirror at a time.[3]
| D5 | k-face | fk | f0 | f1 | f2 | f3 | f4 | k-figure | notes(*) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A4 | ( ) | f0 | 16 | 10 | 30 | 10 | 20 | 5 | 5 | rectified 5-cell | D5/A4 = 16*5!/5! = 16 | |
| A2A1A1 | { } | f1 | 2 | 80 | 6 | 3 | 6 | 3 | 2 | triangular prism | D5/A2A1A1 = 16*5!/3!/2/2 = 80 | |
| A2A1 | {3} | f2 | 3 | 3 | 160 | 1 | 2 | 2 | 1 | Isosceles triangle | D5/A2A1 = 16*5!/3!/2 = 160 | |
| A3A1 | h{4,3} | f3 | 4 | 6 | 4 | 40 | * | 2 | 0 | Segment { } | D5/A3A1 = 16*5!/4!/2 = 40 | |
| A3 | {3,3} | 4 | 6 | 4 | * | 80 | 1 | 1 | Segment { } | D5/A3 = 16*5!/4! = 80 | ||
| D4 | h{4,3,3} | f4 | 8 | 24 | 32 | 8 | 8 | 10 | * | Point ( ) | D5/D4 = 16*5!/8/4! = 10 | |
| A4 | {3,3,3} | 5 | 10 | 10 | 0 | 5 | * | 16 | Point ( ) | D5/A4 = 16*5!/5! = 16 | ||
* = The number of elements (diagonal values) can be computed by the symmetry order D5 divided by the symmetry order of the subgroup with selected mirrors removed.
Projected images
 Perspective projection. |
Images
| Coxeter plane | B5 | |
|---|---|---|
| Graph | 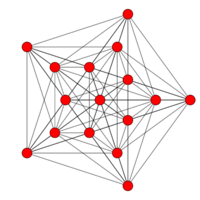
| |
| Dihedral symmetry | [10/2] | |
| Coxeter plane | D5 | D4 |
| Graph | 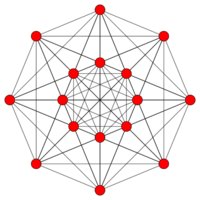
|
|
| Dihedral symmetry | [8] | [6] |
| Coxeter plane | D3 | A3 |
| Graph | 
|

|
| Dihedral symmetry | [4] | [4] |
Related polytopes
It is a part of a dimensional family of uniform polytopes called demihypercubes for being alternation of the hypercube family.
There are 23 Uniform 5-polytopes (uniform 5-polytopes) that can be constructed from the D5 symmetry of the demipenteract, 8 of which are unique to this family, and 15 are shared within the penteractic family.
The 5-demicube is third in a dimensional series of semiregular polytopes. Each progressive uniform polytope is constructed vertex figure of the previous polytope. Thorold Gosset identified this series in 1900 as containing all regular polytope facets, containing all simplexes and orthoplexes (5-simplices and 5-orthoplexes in the case of the 5-demicube). In Coxeter's notation the 5-demicube is given the symbol 121.
References
- ↑ Coxeter, Regular Polytopes, sec 1.8 Configurations
- ↑ Coxeter, Complex Regular Polytopes, p.117
- ↑ Klitzing, Richard. "x3o3o *b3o3o - hin". https://bendwavy.org/klitzing/dimensions/../incmats/hin.htm.
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- H.S.M. Coxeter:
- Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN:0-486-61480-8, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN:978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN:978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)
- Klitzing, Richard. "5D uniform polytopes (polytera) x3o3o *b3o3o - hin". https://bendwavy.org/klitzing/dimensions/polytera.htm.
External links
- Olshevsky, George. "Demipenteract". Glossary for Hyperspace. Archived from the original on 4 February 2007. https://web.archive.org/web/20070204075028/members.aol.com/Polycell/glossary.html#half.
- Multi-dimensional Glossary
Fundamental convex regular and uniform polytopes in dimensions 2–10
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
 |

