Similarity system of triangles

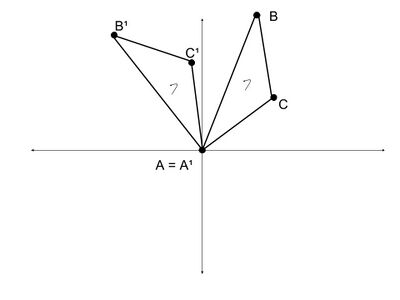
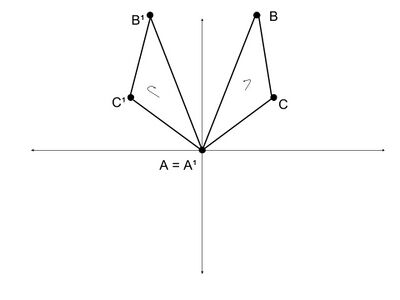
A similarity system of triangles is a specific configuration involving a set of triangles. A set of triangles is considered a configuration when all of the triangles share a minimum of one incidence relation with one of the other triangles present in the set. An incidence relation between triangles refers to when two triangles share a point. For example, the two triangles to the right, [math]\displaystyle{ AHC }[/math] and [math]\displaystyle{ BHC }[/math], are a configuration made up of two incident relations, since points [math]\displaystyle{ C }[/math]and [math]\displaystyle{ H }[/math]are shared. The triangles that make up configurations are known as component triangles. Triangles must not only be a part of a configuration set to be in a similarity system, but must also be directly similar. Direct similarity implies that all angles are equal between two given triangle and that they share the same rotational sense. As is seen in the adjacent images, in the directly similar triangles, the rotation of [math]\displaystyle{ B }[/math] onto [math]\displaystyle{ C }[/math] and [math]\displaystyle{ B^1 }[/math] onto [math]\displaystyle{ C^1 }[/math]occurs in the same direction. In the opposite similar triangles, the rotation of [math]\displaystyle{ B }[/math] onto [math]\displaystyle{ C }[/math] and [math]\displaystyle{ B^1 }[/math] onto [math]\displaystyle{ C^1 }[/math] occurs in the opposite direction. In sum, a configuration is a similarity system when all triangles in the set, lie in the same plane and the following holds true: if there are n triangles in the set and n − 1 triangles are directly similar, then n triangles are directly similar.

Background

J.G. Mauldon introduced the idea of similarity systems of triangles in his paper in Mathematics Magazine "Similar Triangles". Mauldon began his analyses by examining given triangles [math]\displaystyle{ ABC, XYZ }[/math] for direct similarity through complex numbers, specifically the equation [math]\displaystyle{ \begin{vmatrix} a & b & c \\ x & y & z \\ 1 & 1 & 1 \end{vmatrix} = 0 }[/math]. He then furthered his analyses to equilateral triangles, showing that if a triangle [math]\displaystyle{ ABC }[/math] satisfied the equation [math]\displaystyle{ a + wb + w^2c =0 }[/math] when [math]\displaystyle{ w = \frac{-1 + i\surd3}{2} }[/math], it was equilateral. As evidence of this work, he applied his conjectures on direct similarity and equilateral triangles in proving Napoleon's theorem. He then built off Napoleon by proving that if an equilateral triangle was constructed with equilateral triangles incident on each vertex, the midpoints of the connecting lines between the non-incident vertices of the outer three equilateral triangles create an equilateral triangle. Other similar work was done by the French Geometer Thébault in his proof that given a parallelogram and squares that lie on each side of the parallelogram, the centers of the squares create a square. Mauldon then analyzed coplanar sets of triangles, determining if they were similarity systems based on the criterion, if all but one of the triangles were directly similar, then all of the triangles are directly similar.

Examples

Triangles appended to a rectangle

Direct similarity

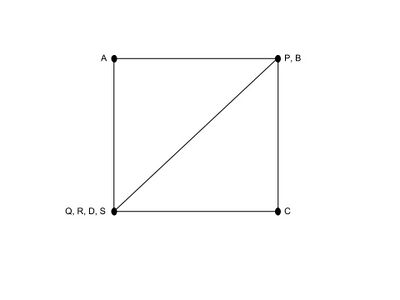
If we construct a rectangle [math]\displaystyle{ ABCD }[/math] with directly similar triangles [math]\displaystyle{ PAB, QBC, RCD, SDA }[/math] on each side of the rectangle that are similar to [math]\displaystyle{ PQS }[/math], then [math]\displaystyle{ RQS }[/math] is directly similar and the set of triangles [math]\displaystyle{ \{PAB, QBC, RCD, SDA, PQS, RQS\} }[/math] is a similarity system.

Indirect similarity

However, if we acknowledge that the triangles can be degenerate and take points [math]\displaystyle{ B }[/math] and [math]\displaystyle{ P }[/math] to lie on each other and [math]\displaystyle{ Q, R, D }[/math]and [math]\displaystyle{ S }[/math] to lie on each other, then the set of triangles is no longer a direct similarity system since the second triangle has area and the others do not.

Rectangular parallelepiped

Given a figure where three sets of lines are parallel, but not equivalent in length (formally known as a rectangular parallelepiped) with all points of order two being labelled as follows:

[math]\displaystyle{ \{A_1B_1C_1, A_2B_2C_2, A_3B_3C_3, A_4B_4C_4, A_1B_4C_3, A_2B_3C_4, A_3B_2C_1, A_4B_1C_2\} }[/math]

Then we can take the above points, analyze them as triangles and we can show that they form a similarity system.

Proof:

In order for any given triangle, [math]\displaystyle{ KLM }[/math], to be directly similar to [math]\displaystyle{ A_1, B_1, C_1 }[/math]the following equation should be satisfied:

[math]\displaystyle{ (\ell-m)a_1+ (m-k)b_1+(k-1)c_1=0. }[/math] where ℓ, m, k, a₁, b₁, and c₁ are sides of triangles.

If the same pattern is followed for the rest of the triangles, one will notice that the summation of the equations for the first four triangles and the summation of the equations for the last four triangles provides the same result. Therefore, by the definition of a similarity system of triangles, no matter the seven similar triangles selected, the eighth will satisfy the system, making them all directly similar.

Gallery

• 

  Direct Similarity Example

• 

  There are two incident relations between triangles AHC and BHC

• 

  Opposite similarity example

• 

  Thébault's theorem

• 

  Napoleon's theorem

• 

  Similarity System Example

• 

  Non-similarity system example

• 

  Rectangular parallelepiped