Simulation decomposition

Short description: A method for visually performing an uncertainty and sensitivity analysis of model output

A typical SimDec output

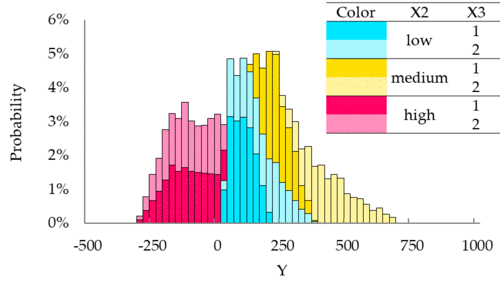
SimDec, or Simulation decomposition, is a hybrid uncertainty and sensitivity analysis method, for visually examining the relationships between the output and input variables of a computational model.

SimDec maps multivariable scenarios onto the distribution of the model output. This visual analytics approach exposes the underlying nature of the model behavior, including its nonlinear and multivariate interaction effects.

SimDec can be used in any range of science, engineering, and social domains. Existing applications include business and environmental issues.

Method

SimDec operates on Monte Carlo simulation (or measured) data where both output and input values are recorded. At least one thousand observations (or simulated iterations) are typically recommended to preserve the readability of the resulting histograms. An outline of the decomposition algorithm, which is readily available in multiple programming languages, proceeds as follows:

1. Select the input variables for decomposition. One can use sensitivity indices (see variance-based sensitivity analysis) to define the most influential variables for decomposition or choose them manually according to the decision-problem context (for example, only those input variables that the decision-maker can act upon). Two to three input variables, ordered by decreasing value of their sensitivity indices, usually provide the most meaningful decomposition results.
2. Divide the inputs into states. The numeric ranges of the inputs are split into several intervals with an equal number of observations in each. For categorical variables, the categories represent states.
3. Form scenarios. All combinations of states of the selected input variables produce unique scenarios or subsets of the data. For example, if the range of X2 is divided into low, medium and high, and X3 takes values of 1 or 2, six scenarios are formed:

   (i) X2 low & X3 = 1,

   (ii) X2 low & X3 = 2,

   (iii) X2 medium & X3 = 1,

   (iv) X2 medium & X3 = 2,

   (v) X2 high & X3 = 1, and

   (vi) X2 high & X3 = 2.

4. Assign scenarios to each output value. The simulation data is used to define the scenario index for each simulation run. For example, if an X2 value falls into the low state and X3 is equal to 2, the corresponding scenario, defined in Step 3, is (ii).
5. Color-code the output distribution. When all output values are assigned scenario indices, they are plotted as series in a stacked histogram, visually separated by color-coding. For ease of visual perception, the states of the most influential input variable are assigned distinct colors, and all the remaining partitions take shades of those colors (see Figure).

All of these steps can be run automatically on the given data using the open-source SimDec packages currently available in Python, R, Julia, and Matlab. A SimDec template in Excel runs a Monte Carlo simulation of a spreadsheet model but possesses only a manual option for input selection.

How to read SimDec

A histogram built for an array of Y = {11, 12, 25, 28, 28, 29, 31, 35, 39, 41}

Histogram

Histogram is an approximate representation of the distribution of numerical data. Its horizontal axis shows the range of the variable of interest, and its vertical axis denotes count, also called frequency, or, if divided by the total number of data points, probability.

The distribution alone can supply only limited information about the data – its minimum, maximum, and shape (where the most of data occurs).

Different degrees of influence of X on Y on a scatter plot and SimDec histogram

Judging the importance of inputs

If an input variable has no effect on the output, its states (e.g., low & high) would lie on top of each other on the SimDec histogram, occupying fully overlapping ranges of the output. If an input variable has a strong effect and explains most of the variance of the output, the border between its states on the SimDec histogram would be vertical. Such visualization has an important decision-making implication – e.g., if the high state of X can be achieved, it would guarantee a certain range of Y. All cases in-between with low-to-strong effects would show a diagonal border between the states. The less they overlap, the larger the effect of X on Y.

While the horizontal displacement of sub-distributions on the SimDec histogram is the key to interpreting the results, the vertical disposition of sub-distributions is just a technical matter of the order of plotting the series of the stacked histogram.

Interpreting the importance of input variables with SimDec histogram

Effect strength	Visual	Decision-making implication
No effect	Sub-distributions are lying on top of each other, occupying fully overlapping ranges of the output.	No matter how we push X, it would have no significant effect on Y.
Moderate effect	The border between sub-distributions is diagonal, there is a partial overall of Y range.	The high state of X improves our chances of getting into high Y, but does not guarantee the result. The same result (overlapping area) can be achieved by having a lower X.
Strong effect	The border between sub-distributions is vertical, no overlap of the Y range.	If the high state of X can be achieved, it would guarantee high Y.

Appearance of different interaction types on SimDec visualization

Exploring the interaction of inputs

When two or more input variables are used for decomposition, it becomes possible to examine their joint effects. A schematic visualization portrays how different types of joint effects of input variables on the output appear on SimDec visualization.

1. No interaction. Sub-distributions of an additive model with both input variables that are equally important would be shifted uniformly. The second-order effect of such inputs would be equal to zero.
2. Linear interaction is a characteristic of multiplicative models. On SimDec, the sub-distributions would be shifted more and more along the horizontal axis. The effect of one input on the output increases with the increasing value of another input. The sensitivity index computed for the second-order effect of such two input variables is non-zero.
3. One input variable switches the direction of influence on the output in different states of another input variable. Such an effect might occur with a sign change in a model. The second-order effect is non-zero.
4. Various types of nonlinear interactions can occur in models. For example, one input variable has no effect on the output in one state of another variable (lying on top of each other red-shaded sub-distributions) but has a strong effect otherwise (shifted blue sub-distributions). Such effect, too, will show up in the non-zero second-order sensitivity index.

Understanding the nature of interaction effects in a computational model and its behavior in general is crucial for effective decision-making.

Limitations

The SimDec method has several limitations:

• It is based on Monte Carlo simulation and thus requires running a computational model a thousand of times or more. To models that take hours to evaluate once, it would be impossible to use SimDec (unless a supercomputer and/or large of time are available).
• SimDec is based on a histogram, thus, for binary or categorical output variables, the visualization would be very limited (e.g., only a few bins).
• The more input variables one selects for the decomposition, the less readable the histogram becomes. Only cases with two and three input variables are presented in.

See also

• Sensitivity analysis
• Data and information visualization
• Histogram
• Interaction (statistics)
• Uncertainty
• Decision making