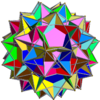
Small dodecicosidodecahedron
| Small dodecicosidodecahedron | |
|---|---|
| |
| Type | Uniform star polyhedron |
| Elements | F = 44, E = 120 V = 60 (χ = −16) |
| Faces by sides | 20{3}+12{5}+12{10} |
| Wythoff symbol | 3/2 5 | 5 3 5/4 | 5 |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U33, C42, W72 |
| Dual polyhedron | Small dodecacronic hexecontahedron |
| Vertex figure | 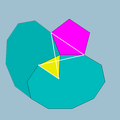 5.10.3/2.10 |
| Bowers acronym | Saddid |
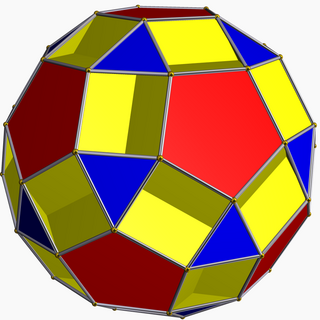
File:Small dodecicosidodecahedron.stl In geometry, the small dodecicosidodecahedron (or small dodekicosidodecahedron) is a nonconvex uniform polyhedron, indexed as U33. It has 44 faces (20 triangles, 12 pentagons, and 12 decagons), 120 edges, and 60 vertices.[1] Its vertex figure is a crossed quadrilateral.
Related polyhedra
It shares its vertex arrangement with the small stellated truncated dodecahedron and the uniform compounds of 6 or 12 pentagrammic prisms. It additionally shares its edge arrangement with the rhombicosidodecahedron (having the triangular and pentagonal faces in common), and with the small rhombidodecahedron (having the decagonal faces in common).
 Rhombicosidodecahedron |
 Small dodecicosidodecahedron |
 Small rhombidodecahedron |
 Small stellated truncated dodecahedron |
 Compound of six pentagrammic prisms |
 Compound of twelve pentagrammic prisms |
Dual
| Small dodecacronic hexecontahedron | |
|---|---|

| |
| Type | Star polyhedron |
| Face | 
|
| Elements | F = 60, E = 120 V = 44 (χ = −16) |
| Symmetry group | Ih, [5,3], *532 |
| Index references | DU33 |
| dual polyhedron | Small dodecicosidodecahedron |
File:Small dodecacronic hexecontahedron.stl The dual polyhedron to the small dodecicosidodecahedron is the small dodecacronic hexecontahedron (or small sagittal ditriacontahedron). It is visually identical to the small rhombidodecacron. Its faces are darts. A part of each dart lies inside the solid, hence is invisible in solid models.
Proportions
Faces have two angles of [math]\displaystyle{ \arccos(\frac{5}{8}+\frac{1}{8}\sqrt{5})\approx 25.242\,832\,961\,52^{\circ} }[/math], one of [math]\displaystyle{ \arccos(-\frac{1}{8}+\frac{9}{40}\sqrt{5})\approx 67.783\,011\,547\,44^{\circ} }[/math] and one of [math]\displaystyle{ 360^{\circ}-\arccos(-\frac{1}{4}-\frac{1}{10}\sqrt{5})\approx 241.731\,322\,529\,52^{\circ} }[/math]. Its dihedral angles equal [math]\displaystyle{ \arccos({\frac{-19-8\sqrt{5}}{41}})\approx 154.121\,363\,125\,78^{\circ} }[/math]. The ratio between the lengths of the long and short edges is [math]\displaystyle{ \frac{7+\sqrt{5}}{6}\approx 1.539\,344\,662\,92 }[/math].
References
- Coxeter, H. S. M. (May 13, 1954). "Uniform Polyhedra". Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 246 (916): 401–450. doi:10.1098/rsta.1954.0003.
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9. OCLC 1738087.
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5
External links
- Weisstein, Eric W.. "Uniform Polyhedron". http://mathworld.wolfram.com/UniformPolyhedron.html.
- Weisstein, Eric W.. "Small dodecicosidodecahedron". http://mathworld.wolfram.com/SmallDodecicosidodecahedron.html.
- Weisstein, Eric W.. "Small dodecacronic hexecontahedron". http://mathworld.wolfram.com/SmallDodecacronicHexecontahedron.html.
 |

