Spectral flatness
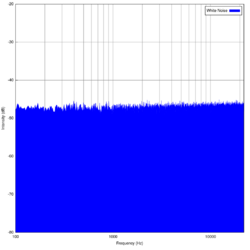
Spectral flatness or tonality coefficient,[1][2] also known as Wiener entropy,[3][4] is a measure used in digital signal processing to characterize an audio spectrum. Spectral flatness is typically measured in decibels, and provides a way to quantify how much a sound resembles a pure tone, as opposed to being noise-like.[2]
Interpretation
The meaning of tonal in this context is in the sense of the amount of peaks or resonant structure in a power spectrum, as opposed to flat spectrum of a white noise. A high spectral flatness (approaching 1.0 for white noise) indicates that the spectrum has a similar amount of power in all spectral bands — this would sound similar to white noise, and the graph of the spectrum would appear relatively flat and smooth. A low spectral flatness (approaching 0.0 for a pure tone) indicates that the spectral power is concentrated in a relatively small number of bands — this would typically sound like a mixture of sine waves, and the spectrum would appear "spiky".[5]
Dubnov [2] has shown that spectral flatness is equivalent to information theoretic concept of mutual information that is known as dual total correlation.
Formulation
The spectral flatness is calculated by dividing the geometric mean of the power spectrum by the arithmetic mean of the power spectrum, i.e.:
- [math]\displaystyle{ \mathrm{Flatness} = \frac{\sqrt[N]{\prod_{n=0}^{N-1}x(n)}}{\frac{\sum_{n=0}^{N-1}x(n)}{N}} = \frac{\exp\left(\frac{1}{N}\sum_{n=0}^{N-1} \ln x(n)\right)}{\frac{1}{N} \sum_{n=0}^{N-1}x(n)} }[/math]
where x(n) represents the magnitude of bin number n. Note that a single (or more) empty bin yields a flatness of 0, so this measure is most useful when bins are generally not empty.
The ratio produced by this calculation is often converted to a decibel scale for reporting, with a maximum of 0 dB and a minimum of −∞ dB.
The spectral flatness can also be measured within a specified sub-band, rather than across the whole band.
Applications
This measurement is one of the many audio descriptors used in the MPEG-7 standard, in which it is labelled "AudioSpectralFlatness".
In birdsong research, it has been used as one of the features measured on birdsong audio, when testing similarity between two excerpts.[6] Spectral flatness has also been used in the analysis of electroencephalography (EEG) diagnostics and research,[7] and psychoacoustics in humans.[8]
References
- ↑ J. D. Johnston (1988). "Transform coding of audio signals using perceptual noise criteria". IEEE Journal on Selected Areas in Communications 6 (2): 314–332. doi:10.1109/49.608.
- ↑ 2.0 2.1 2.2 Shlomo Dubnov (2004). "Generalization of Spectral Flatness Measure for Non-Gaussian Linear Processes". Signal Processing Letters 11 (8): 698–701. doi:10.1109/LSP.2004.831663. ISSN 1070-9908. Bibcode: 2004ISPL...11..698D.
- ↑ The Song Features › Wiener entropy "defined as the ratio of geometric mean to arithmetic mean of the spectrum"
- ↑ Luscinia parameters "Wiener entropy is an alternative measure of the noisiness of a signal. It is defined as the ratio of the geometric mean to the arithmetic mean of the power spectrum."
- ↑ A Large Set of Audio Features for Sound Description - technical report published by IRCAM in 2003. Section 9.1
- ↑ Tchernichovski, O., Nottebohm, F., Ho, C. E., Pesaran, B., Mitra, P. P., 2000. A procedure for an automated measurement of song similarity. Animal Behaviour 59 (6), 1167–1176, doi:10.1006/anbe.1999.1416.
- ↑ Burns, T.; Rajan, R. (2015). "Burns & Rajan (2015) Combining complexity measures of EEG data: multiplying measures reveal previously hidden information. F1000Research. 4:137.". F1000Research 4: 137. doi:10.12688/f1000research.6590.1. PMID 26594331.
- ↑ Burns, T.; Rajan, R. (2019). "A Mathematical Approach to Correlating Objective Spectro-Temporal Features of Non-linguistic Sounds With Their Subjective Perceptions in Humans". Frontiers in Neuroscience 13: 794. doi:10.3389/fnins.2019.00794. PMID 31417350.
 |  |
