Mutual information
| Information theory |
|---|
 |

In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual dependence between the two variables. More specifically, it quantifies the "amount of information" (in units such as shannons (bits), nats or hartleys) obtained about one random variable by observing the other random variable. The concept of mutual information is intimately linked to that of entropy of a random variable, a fundamental notion in information theory that quantifies the expected "amount of information" held in a random variable.
Not limited to real-valued random variables and linear dependence like the correlation coefficient, MI is more general and determines how different the joint distribution of the pair is from the product of the marginal distributions of and . MI is the expected value of the pointwise mutual information (PMI).
The quantity was defined and analyzed by Claude Shannon in his landmark paper "A Mathematical Theory of Communication", although he did not call it "mutual information". This term was coined later by Robert Fano.[2] Mutual Information is also known as information gain.
Definition
Let be a pair of random variables with values over the space . If their joint distribution is and the marginal distributions are and , the mutual information is defined as
where is the Kullback–Leibler divergence, and is the outer product distribution which assigns probability to each .
Expressed in terms of the entropy and the conditional entropy of the random variables and , one also has (See relation to conditional and joint entropy):
Notice, as per property of the Kullback–Leibler divergence, that is equal to zero precisely when the joint distribution coincides with the product of the marginals, i.e. when and are independent (and hence observing tells you nothing about ). is non-negative, it is a measure of the price for encoding as a pair of independent random variables when in reality they are not.
If the natural logarithm is used, the unit of mutual information is the nat. If the log base 2 is used, the unit of mutual information is the shannon, also known as the bit. If the log base 10 is used, the unit of mutual information is the hartley, also known as the ban or the dit.
In terms of PMFs for discrete distributions
The mutual information of two jointly discrete random variables and is calculated as a double sum:[3]: 20
- ,
where is the joint probability mass function of and , and and are the marginal probability mass functions of and respectively.
In terms of PDFs for continuous distributions
In the case of jointly continuous random variables, the double sum is replaced by a double integral:[3]: 251
- ,
where is now the joint probability density function of and , and and are the marginal probability density functions of and respectively.
Motivation
Intuitively, mutual information measures the information that and share: It measures how much knowing one of these variables reduces uncertainty about the other. For example, if and are independent, then knowing does not give any information about and vice versa, so their mutual information is zero. At the other extreme, if is a deterministic function of and is a deterministic function of then all information conveyed by is shared with : knowing determines the value of and vice versa. As a result, the mutual information is the same as the uncertainty contained in (or ) alone, namely the entropy of (or ). A very special case of this is when and are the same random variable.
Mutual information is a measure of the inherent dependence expressed in the joint distribution of and relative to the marginal distribution of and under the assumption of independence. Mutual information therefore measures dependence in the following sense: if and only if and are independent random variables. This is easy to see in one direction: if and are independent, then , and therefore:
- .
Moreover, mutual information is nonnegative (i.e. see below) and symmetric (i.e. see below).
Properties
Nonnegativity
Using Jensen's inequality on the definition of mutual information we can show that is non-negative, i.e.[3]: 28
Symmetry
The proof is given considering the relationship with entropy, as shown below.
Supermodularity under independence
If is independent of , then
- .[4]
Relation to conditional and joint entropy
Mutual information can be equivalently expressed as:
where and are the marginal entropies, and are the conditional entropies, and is the joint entropy of and .
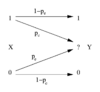
Notice the analogy to the union, difference, and intersection of two sets: in this respect, all the formulas given above are apparent from the Venn diagram reported at the beginning of the article.
In terms of a communication channel in which the output is a noisy version of the input , these relations are summarised in the figure:

Because is non-negative, consequently, . Here we give the detailed deduction of for the case of jointly discrete random variables:
The proofs of the other identities above are similar. The proof of the general case (not just discrete) is similar, with integrals replacing sums.
Intuitively, if entropy is regarded as a measure of uncertainty about a random variable, then is a measure of what does not say about . This is "the amount of uncertainty remaining about after is known", and thus the right side of the second of these equalities can be read as "the amount of uncertainty in , minus the amount of uncertainty in which remains after is known", which is equivalent to "the amount of uncertainty in which is removed by knowing ". This corroborates the intuitive meaning of mutual information as the amount of information (that is, reduction in uncertainty) that knowing either variable provides about the other.
Note that in the discrete case and therefore . Thus , and one can formulate the basic principle that a variable contains at least as much information about itself as any other variable can provide.
Relation to Kullback–Leibler divergence
For jointly discrete or jointly continuous pairs , mutual information is the Kullback–Leibler divergence from the product of the marginal distributions, , of the joint distribution , that is,
Furthermore, let be the conditional mass or density function. Then, we have the identity
The proof for jointly discrete random variables is as follows:
Similarly this identity can be established for jointly continuous random variables.
Note that here the Kullback–Leibler divergence involves integration over the values of the random variable only, and the expression still denotes a random variable because is random. Thus mutual information can also be understood as the expectation over of the Kullback–Leibler divergence of the conditional distribution of given from the univariate distribution of : the more different the distributions and are on average, the greater the information gain.
Bayesian estimation of mutual information
If samples from a joint distribution are available, a Bayesian approach can be used to estimate the mutual information of that distribution. The first work to do this, which also showed how to do Bayesian estimation of many other information-theoretic properties besides mutual information, was.[5] Subsequent researchers have rederived [6] and extended [7] this analysis. See [8] for a recent paper based on a prior specifically tailored to estimation of mutual information per se. Besides, recently an estimation method accounting for continuous and multivariate outputs, , was proposed in .[9]
Independence assumptions
The Kullback-Leibler divergence formulation of the mutual information is predicated on that one is interested in comparing to the fully factorized outer product . In many problems, such as non-negative matrix factorization, one is interested in less extreme factorizations; specifically, one wishes to compare to a low-rank matrix approximation in some unknown variable ; that is, to what degree one might have
Alternately, one might be interested in knowing how much more information carries over its factorization. In such a case, the excess information that the full distribution carries over the matrix factorization is given by the Kullback-Leibler divergence
The conventional definition of the mutual information is recovered in the extreme case that the process has only one value for .
Variations
Several variations on mutual information have been proposed to suit various needs. Among these are normalized variants and generalizations to more than two variables.
Metric
Many applications require a metric, that is, a distance measure between pairs of points. The quantity
satisfies the properties of a metric (triangle inequality, non-negativity, indiscernability and symmetry), where equality is understood to mean that can be completely determined from .[10]
This distance metric is also known as the variation of information.
If are discrete random variables then all the entropy terms are non-negative, so and one can define a normalized distance
Plugging in the definitions shows that
This is known as the Rajski Distance.[11] In a set-theoretic interpretation of information (see the figure for Conditional entropy), this is effectively the Jaccard distance between and .
Finally,
is also a metric.
Conditional mutual information
Sometimes it is useful to express the mutual information of two random variables conditioned on a third.
For jointly discrete random variables this takes the form
which can be simplified as
For jointly continuous random variables this takes the form
which can be simplified as
Conditioning on a third random variable may either increase or decrease the mutual information, but it is always true that
for discrete, jointly distributed random variables . This result has been used as a basic building block for proving other inequalities in information theory.
Interaction information
Several generalizations of mutual information to more than two random variables have been proposed, such as total correlation (or multi-information) and dual total correlation. The expression and study of multivariate higher-degree mutual information was achieved in two seemingly independent works: McGill (1954)[12] who called these functions "interaction information", and Hu Kuo Ting (1962).[13] Interaction information is defined for one variable as follows:
and for
Some authors reverse the order of the terms on the right-hand side of the preceding equation, which changes the sign when the number of random variables is odd. (And in this case, the single-variable expression becomes the negative of the entropy.) Note that
Multivariate statistical independence
The multivariate mutual information functions generalize the pairwise independence case that states that if and only if , to arbitrary numerous variable. n variables are mutually independent if and only if the mutual information functions vanish with (theorem 2[14]). In this sense, the can be used as a refined statistical independence criterion.
Applications
For 3 variables, Brenner et al. applied multivariate mutual information to neural coding and called its negativity "synergy"[15] and Watkinson et al. applied it to genetic expression.[16] For arbitrary k variables, Tapia et al. applied multivariate mutual information to gene expression.[17][14] It can be zero, positive, or negative.[13] The positivity corresponds to relations generalizing the pairwise correlations, nullity corresponds to a refined notion of independence, and negativity detects high dimensional "emergent" relations and clusterized datapoints [17]).
One high-dimensional generalization scheme which maximizes the mutual information between the joint distribution and other target variables is found to be useful in feature selection.[18]
Mutual information is also used in the area of signal processing as a measure of similarity between two signals. For example, FMI metric[19] is an image fusion performance measure that makes use of mutual information in order to measure the amount of information that the fused image contains about the source images. The Matlab code for this metric can be found at.[20] A python package for computing all multivariate mutual informations, conditional mutual information, joint entropies, total correlations, information distance in a dataset of n variables is available.[21]
Directed information
Directed information, , measures the amount of information that flows from the process to , where denotes the vector and denotes . The term directed information was coined by James Massey and is defined as
- .
Note that if , the directed information becomes the mutual information. Directed information has many applications in problems where causality plays an important role, such as capacity of channel with feedback.[22][23]
Normalized variants
Normalized variants of the mutual information are provided by the coefficients of constraint,[24] uncertainty coefficient[25] or proficiency:[26]
The two coefficients have a value ranging in [0, 1], but are not necessarily equal. This measure is not symmetric. If one desires a symmetric measure they can consider the following redundancy measure:
which attains a minimum of zero when the variables are independent and a maximum value of
when one variable becomes completely redundant with the knowledge of the other. See also Redundancy (information theory).
Another symmetrical measure is the symmetric uncertainty (Witten Frank), given by
which represents the harmonic mean of the two uncertainty coefficients .[25]
If we consider mutual information as a special case of the total correlation or dual total correlation, the normalized version are respectively,
- and
This normalized version also known as Information Quality Ratio (IQR) which quantifies the amount of information of a variable based on another variable against total uncertainty:[27]
There exists a normalization[28] which derives from first thinking of mutual information as an analogue to covariance (thus Shannon entropy is analogous to variance). Then the normalized mutual information is calculated akin to the Pearson correlation coefficient,
Weighted variants
In the traditional formulation of the mutual information,
each event or object specified by is weighted by the corresponding probability . This assumes that all objects or events are equivalent apart from their probability of occurrence. However, in some applications it may be the case that certain objects or events are more significant than others, or that certain patterns of association are more semantically important than others.
For example, the deterministic mapping may be viewed as stronger than the deterministic mapping , although these relationships would yield the same mutual information. This is because the mutual information is not sensitive at all to any inherent ordering in the variable values (Cronbach 1954, Coombs, Dawes & Tversky 1970, Lockhead 1970), and is therefore not sensitive at all to the form of the relational mapping between the associated variables. If it is desired that the former relation—showing agreement on all variable values—be judged stronger than the later relation, then it is possible to use the following weighted mutual information (Guiasu 1977).
which places a weight on the probability of each variable value co-occurrence, . This allows that certain probabilities may carry more or less significance than others, thereby allowing the quantification of relevant holistic or Prägnanz factors. In the above example, using larger relative weights for , , and would have the effect of assessing greater informativeness for the relation than for the relation , which may be desirable in some cases of pattern recognition, and the like. This weighted mutual information is a form of weighted KL-Divergence, which is known to take negative values for some inputs,[29] and there are examples where the weighted mutual information also takes negative values.[30]
Adjusted mutual information
A probability distribution can be viewed as a partition of a set. One may then ask: if a set were partitioned randomly, what would the distribution of probabilities be? What would the expectation value of the mutual information be? The adjusted mutual information or AMI subtracts the expectation value of the MI, so that the AMI is zero when two different distributions are random, and one when two distributions are identical. The AMI is defined in analogy to the adjusted Rand index of two different partitions of a set.
Absolute mutual information
Using the ideas of Kolmogorov complexity, one can consider the mutual information of two sequences independent of any probability distribution:
To establish that this quantity is symmetric up to a logarithmic factor () one requires the chain rule for Kolmogorov complexity (Li Vitányi). Approximations of this quantity via compression can be used to define a distance measure to perform a hierarchical clustering of sequences without having any domain knowledge of the sequences (Cilibrasi Vitányi).
Linear correlation
Unlike correlation coefficients, such as the product moment correlation coefficient, mutual information contains information about all dependence—linear and nonlinear—and not just linear dependence as the correlation coefficient measures. However, in the narrow case that the joint distribution for and is a bivariate normal distribution (implying in particular that both marginal distributions are normally distributed), there is an exact relationship between and the correlation coefficient (Gel'fand Yaglom).
The equation above can be derived as follows for a bivariate Gaussian:
Therefore,
For discrete data
When and are limited to be in a discrete number of states, observation data is summarized in a contingency table, with row variable (or ) and column variable (or ). Mutual information is one of the measures of association or correlation between the row and column variables.
Other measures of association include Pearson's chi-squared test statistics, G-test statistics, etc. In fact, with the same log base, mutual information will be equal to the G-test log-likelihood statistic divided by , where is the sample size.
Applications
In many applications, one wants to maximize mutual information (thus increasing dependencies), which is often equivalent to minimizing conditional entropy. Examples include:
- In search engine technology, mutual information between phrases and contexts is used as a feature for k-means clustering to discover semantic clusters (concepts).[31] For example, the mutual information of a bigram might be calculated as:
- where is the number of times the bigram xy appears in the corpus, is the number of times the unigram x appears in the corpus, B is the total number of bigrams, and U is the total number of unigrams.[31]
- In telecommunications, the channel capacity is equal to the mutual information, maximized over all input distributions.
- Discriminative training procedures for hidden Markov models have been proposed based on the maximum mutual information (MMI) criterion.
- RNA secondary structure prediction from a multiple sequence alignment.
- Phylogenetic profiling prediction from pairwise present and disappearance of functionally link genes.
- Mutual information has been used as a criterion for feature selection and feature transformations in machine learning. It can be used to characterize both the relevance and redundancy of variables, such as the minimum redundancy feature selection.
- Mutual information is used in determining the similarity of two different clusterings of a dataset. As such, it provides some advantages over the traditional Rand index.
- Mutual information of words is often used as a significance function for the computation of collocations in corpus linguistics. This has the added complexity that no word-instance is an instance to two different words; rather, one counts instances where 2 words occur adjacent or in close proximity; this slightly complicates the calculation, since the expected probability of one word occurring within words of another, goes up with
- Mutual information is used in medical imaging for image registration. Given a reference image (for example, a brain scan), and a second image which needs to be put into the same coordinate system as the reference image, this image is deformed until the mutual information between it and the reference image is maximized.
- Detection of phase synchronization in time series analysis.
- In the infomax method for neural-net and other machine learning, including the infomax-based Independent component analysis algorithm
- Average mutual information in delay embedding theorem is used for determining the embedding delay parameter.
- Mutual information between genes in expression microarray data is used by the ARACNE algorithm for reconstruction of gene networks.
- In statistical mechanics, Loschmidt's paradox may be expressed in terms of mutual information.[32][33] Loschmidt noted that it must be impossible to determine a physical law which lacks time reversal symmetry (e.g. the second law of thermodynamics) only from physical laws which have this symmetry. He pointed out that the H-theorem of Boltzmann made the assumption that the velocities of particles in a gas were permanently uncorrelated, which removed the time symmetry inherent in the H-theorem. It can be shown that if a system is described by a probability density in phase space, then Liouville's theorem implies that the joint information (negative of the joint entropy) of the distribution remains constant in time. The joint information is equal to the mutual information plus the sum of all the marginal information (negative of the marginal entropies) for each particle coordinate. Boltzmann's assumption amounts to ignoring the mutual information in the calculation of entropy, which yields the thermodynamic entropy (divided by the Boltzmann constant).
- In stochastic processes coupled to changing environments, mutual information can be used to disentangle internal and effective environmental dependencies.[34][35] This is particularly useful when a physical system undergoes changes in the parameters describing its dynamics, e.g., changes in temperature.
- The mutual information is used to learn the structure of Bayesian networks/dynamic Bayesian networks, which is thought to explain the causal relationship between random variables, as exemplified by the GlobalMIT toolkit:[36] learning the globally optimal dynamic Bayesian network with the Mutual Information Test criterion.
- The mutual information is used to quantify information transmitted during the updating procedure in the Gibbs sampling algorithm.[37]
- Popular cost function in decision tree learning.
- The mutual information is used in cosmology to test the influence of large-scale environments on galaxy properties in the Galaxy Zoo.
- The mutual information was used in Solar Physics to derive the solar differential rotation profile, a travel-time deviation map for sunspots, and a time–distance diagram from quiet-Sun measurements[38]
- Used in Invariant Information Clustering to automatically train neural network classifiers and image segmenters given no labelled data.[39]
- In stochastic dynamical systems with multiple timescales, mutual information has been shown to capture the functional couplings between different temporal scales.[40] Importantly, it was shown that physical interactions may or may not give rise to mutual information, depending on the typical timescale of their dynamics.
See also
Notes
- ↑ Cover, Thomas M.; Thomas, Joy A. (2005). Elements of information theory. John Wiley & Sons, Ltd. pp. 13–55. ISBN 978-0-471-74882-3. http://www.cs.columbia.edu/~vh/courses/LexicalSemantics/Association/Cover&Thomas-Ch2.pdf.
- ↑ Kreer, J. G. (1957). "A question of terminology". IRE Transactions on Information Theory 3 (3): 208. doi:10.1109/TIT.1957.1057418.
- ↑ 3.0 3.1 3.2 Cover, T.M.; Thomas, J.A. (1991). Elements of Information Theory (Wiley ed.). John Wiley & Sons. ISBN 978-0-471-24195-9. https://archive.org/details/elementsofinform0000cove.
- ↑ Janssen, Joseph; Guan, Vincent; Robeva, Elina (2023). "Ultra-marginal Feature Importance: Learning from Data with Causal Guarantees". International Conference on Artificial Intelligence and Statistics: 10782–10814. https://proceedings.mlr.press/v206/janssen23a.html.
- ↑ Wolpert, D.H.; Wolf, D.R. (1995). "Estimating functions of probability distributions from a finite set of samples". Physical Review E 52 (6): 6841–6854. doi:10.1103/PhysRevE.52.6841. PMID 9964199. Bibcode: 1995PhRvE..52.6841W.
- ↑ Hutter, M. (2001). "Distribution of Mutual Information". Advances in Neural Information Processing Systems.
- ↑ Archer, E.; Park, I.M.; Pillow, J. (2013). "Bayesian and Quasi-Bayesian Estimators for Mutual Information from Discrete Data". Entropy 15 (12): 1738–1755. doi:10.3390/e15051738. Bibcode: 2013Entrp..15.1738A.
- ↑ Wolpert, D.H; DeDeo, S. (2013). "Estimating Functions of Distributions Defined over Spaces of Unknown Size". Entropy 15 (12): 4668–4699. doi:10.3390/e15114668. Bibcode: 2013Entrp..15.4668W.
- ↑ Tomasz Jetka; Karol Nienaltowski; Tomasz Winarski; Slawomir Blonski; Michal Komorowski (2019), "Information-theoretic analysis of multivariate single-cell signaling responses", PLOS Computational Biology 15 (7), doi:10.1371/journal.pcbi.1007132, PMID 31299056, Bibcode: 2019PLSCB..15E7132J
- ↑ Rajski, C. (1961). "A metric space of discrete probability distributions". Information and Control 4 (4): 371–377. doi:10.1016/S0019-9958(61)80055-7.
- ↑ Rajski, C. (1961). "A metric space of discrete probability distributions". Information and Control 4 (4): 371–377. doi:10.1016/S0019-9958(61)80055-7.
- ↑ McGill, W. (1954). "Multivariate information transmission". Psychometrika 19 (1): 97–116. doi:10.1007/BF02289159.
- ↑ 13.0 13.1 Hu, K.T. (1962). "On the Amount of Information". Theory Probab. Appl. 7 (4): 439–447. doi:10.1137/1107041.
- ↑ 14.0 14.1 Baudot, P.; Tapia, M.; Bennequin, D.; Goaillard, J.M. (2019). "Topological Information Data Analysis". Entropy 21 (9): 869. doi:10.3390/e21090869. Bibcode: 2019Entrp..21..869B.
- ↑ Brenner, N.; Strong, S.; Koberle, R.; Bialek, W. (2000). "Synergy in a Neural Code". Neural Comput 12 (7): 1531–1552. doi:10.1162/089976600300015259. PMID 10935917.
- ↑ Watkinson, J.; Liang, K.; Wang, X.; Zheng, T.; Anastassiou, D. (2009). "Inference of Regulatory Gene Interactions from Expression Data Using Three-Way Mutual Information". Chall. Syst. Biol. Ann. N. Y. Acad. Sci. 1158 (1): 302–313. doi:10.1111/j.1749-6632.2008.03757.x. PMID 19348651. Bibcode: 2009NYASA1158..302W.
- ↑ 17.0 17.1 Tapia, M.; Baudot, P.; Formizano-Treziny, C.; Dufour, M.; Goaillard, J.M. (2018). "Neurotransmitter identity and electrophysiological phenotype are genetically coupled in midbrain dopaminergic neurons". Sci. Rep. 8 (1): 13637. doi:10.1038/s41598-018-31765-z. PMID 30206240. Bibcode: 2018NatSR...813637T.
- ↑ Christopher D. Manning; Prabhakar Raghavan; Hinrich Schütze (2008). An Introduction to Information Retrieval. Cambridge University Press. ISBN 978-0-521-86571-5.
- ↑ Haghighat, M. B. A.; Aghagolzadeh, A.; Seyedarabi, H. (2011). "A non-reference image fusion metric based on mutual information of image features". Computers & Electrical Engineering 37 (5): 744–756. doi:10.1016/j.compeleceng.2011.07.012.
- ↑ "Feature Mutual Information (FMI) metric for non-reference image fusion - File Exchange - MATLAB Central". http://www.mathworks.com/matlabcentral/fileexchange/45926-feature-mutual-information-fmi-image-fusion-metric.
- ↑ "InfoTopo: Topological Information Data Analysis. Deep statistical unsupervised and supervised learning - File Exchange - Github". https://infotopo.readthedocs.io/en/latest/index.html.
- ↑ Massey, James (1990). "Causality, Feedback And Directed Informatio".
- ↑ Permuter, Haim Henry; Weissman, Tsachy; Goldsmith, Andrea J. (February 2009). "Finite State Channels With Time-Invariant Deterministic Feedback". IEEE Transactions on Information Theory 55 (2): 644–662. doi:10.1109/TIT.2008.2009849.
- ↑ Coombs, Dawes & Tversky 1970.
- ↑ 25.0 25.1 Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Section 14.7.3. Conditional Entropy and Mutual Information". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8. http://apps.nrbook.com/empanel/index.html#pg=758. Retrieved 2011-08-13.
- ↑ White, Jim; Steingold, Sam; Fournelle, Connie. "Performance Metrics for Group-Detection Algorithms". Interface 2004. http://www.interfacesymposia.org/I04/I2004Proceedings/WhiteJim/WhiteJim.paper.pdf. Retrieved 2014-02-19.
- ↑ Wijaya, Dedy Rahman; Sarno, Riyanarto; Zulaika, Enny (2017). "Information Quality Ratio as a novel metric for mother wavelet selection". Chemometrics and Intelligent Laboratory Systems 160: 59–71. doi:10.1016/j.chemolab.2016.11.012.
- ↑ Strehl, Alexander; Ghosh, Joydeep (2003). "Cluster Ensembles – A Knowledge Reuse Framework for Combining Multiple Partitions". The Journal of Machine Learning Research 3: 583–617. doi:10.1162/153244303321897735. http://www.jmlr.org/papers/volume3/strehl02a/strehl02a.pdf.
- ↑ Kvålseth, T. O. (1991). "The relative useful information measure: some comments". Information Sciences 56 (1): 35–38. doi:10.1016/0020-0255(91)90022-m.
- ↑ Pocock, A. (2012). Feature Selection Via Joint Likelihood (PDF) (Thesis).
- ↑ 31.0 31.1 Parsing a Natural Language Using Mutual Information Statistics by David M. Magerman and Mitchell P. Marcus
- ↑ Hugh Everett Theory of the Universal Wavefunction, Thesis, Princeton University, (1956, 1973), pp 1–140 (page 30)
- ↑ Everett, Hugh (1957). "Relative State Formulation of Quantum Mechanics". Reviews of Modern Physics 29 (3): 454–462. doi:10.1103/revmodphys.29.454. Bibcode: 1957RvMP...29..454E. http://www.univer.omsk.su/omsk/Sci/Everett/paper1957.html. Retrieved 2012-07-16.
- ↑ Nicoletti, Giorgio; Busiello, Daniel Maria (2021-11-22). "Mutual Information Disentangles Interactions from Changing Environments". Physical Review Letters 127 (22). doi:10.1103/PhysRevLett.127.228301. PMID 34889638. Bibcode: 2021PhRvL.127v8301N. https://link.aps.org/doi/10.1103/PhysRevLett.127.228301.
- ↑ Nicoletti, Giorgio; Busiello, Daniel Maria (2022-07-29). "Mutual information in changing environments: Nonlinear interactions, out-of-equilibrium systems, and continuously varying diffusivities". Physical Review E 106 (1). doi:10.1103/PhysRevE.106.014153. PMID 35974654. Bibcode: 2022PhRvE.106a4153N. https://link.aps.org/doi/10.1103/PhysRevE.106.014153.
- ↑ GlobalMIT at Google Code
- ↑ Lee, Se Yoon (2021). "Gibbs sampler and coordinate ascent variational inference: A set-theoretical review". Communications in Statistics - Theory and Methods 51 (6): 1549–1568. doi:10.1080/03610926.2021.1921214.
- ↑ Keys, Dustin; Kholikov, Shukur; Pevtsov, Alexei A. (February 2015). "Application of Mutual Information Methods in Time Distance Helioseismology". Solar Physics 290 (3): 659–671. doi:10.1007/s11207-015-0650-y. Bibcode: 2015SoPh..290..659K.
- ↑ Invariant Information Clustering for Unsupervised Image Classification and Segmentation by Xu Ji, Joao Henriques and Andrea Vedaldi
- ↑ Nicoletti, Giorgio; Busiello, Daniel Maria (2024-04-08). "Information Propagation in Multilayer Systems with Higher-Order Interactions across Timescales". Physical Review X 14 (2). doi:10.1103/PhysRevX.14.021007. Bibcode: 2024PhRvX..14b1007N. https://link.aps.org/doi/10.1103/PhysRevX.14.021007.
References
- Baudot, P.; Tapia, M.; Bennequin, D.; Goaillard, J.M. (2019). "Topological Information Data Analysis". Entropy 21 (9): 869. doi:10.3390/e21090869. Bibcode: 2019Entrp..21..869B.
- Cilibrasi, R.; Vitányi, Paul (2005). "Clustering by compression". IEEE Transactions on Information Theory 51 (4): 1523–1545. doi:10.1109/TIT.2005.844059. http://www.cwi.nl/~paulv/papers/cluster.pdf.
- Cronbach, L. J. (1954). "On the non-rational application of information measures in psychology". in Quastler, Henry. Information Theory in Psychology: Problems and Methods. Glencoe, Illinois: Free Press. pp. 14–30.
- Coombs, C. H.; Dawes, R. M.; Tversky, A. (1970). Mathematical Psychology: An Elementary Introduction. Englewood Cliffs, New Jersey: Prentice-Hall.
- Church, Kenneth Ward; Hanks, Patrick (1989). "Word association norms, mutual information, and lexicography". Proceedings of the 27th Annual Meeting of the Association for Computational Linguistics 16 (1): 76–83. doi:10.3115/981623.981633.
- Gel'fand, I.M.; Yaglom, A.M. (1957). "Calculation of amount of information about a random function contained in another such function". American Mathematical Society Translations. Series 2 12: 199–246. doi:10.1090/trans2/012/09. ISBN 978-0-8218-1712-4. English translation of original in Uspekhi Matematicheskikh Nauk 12 (1): 3-52.
- Guiasu, Silviu (1977). Information Theory with Applications. McGraw-Hill, New York. ISBN 978-0-07-025109-0.
- Li, Ming; Vitányi, Paul (February 1997). An introduction to Kolmogorov complexity and its applications. New York: Springer-Verlag. ISBN 978-0-387-94868-3.
- Lockhead, G. R. (1970). "Identification and the form of multidimensional discrimination space". Journal of Experimental Psychology 85 (1): 1–10. doi:10.1037/h0029508. PMID 5458322.
- David J. C. MacKay. Information Theory, Inference, and Learning Algorithms Cambridge: Cambridge University Press, 2003. ISBN 0-521-64298-1 (available free online)
- Haghighat, M. B. A.; Aghagolzadeh, A.; Seyedarabi, H. (2011). "A non-reference image fusion metric based on mutual information of image features". Computers & Electrical Engineering 37 (5): 744–756. doi:10.1016/j.compeleceng.2011.07.012.
- Athanasios Papoulis. Probability, Random Variables, and Stochastic Processes, second edition. New York: McGraw-Hill, 1984. (See Chapter 15.)
- Witten, Ian H.; Frank, Eibe (2005). Data Mining: Practical Machine Learning Tools and Techniques. Morgan Kaufmann, Amsterdam. ISBN 978-0-12-374856-0. http://www.cs.waikato.ac.nz/~ml/weka/book.html.
- Peng, H.C.; Long, F.; Ding, C. (2005). "Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy". IEEE Transactions on Pattern Analysis and Machine Intelligence 27 (8): 1226–1238. doi:10.1109/tpami.2005.159. PMID 16119262. http://research.janelia.org/peng/proj/mRMR/index.htm.
- Andre S. Ribeiro; Stuart A. Kauffman; Jason Lloyd-Price; Bjorn Samuelsson; Joshua Socolar (2008). "Mutual Information in Random Boolean models of regulatory networks". Physical Review E 77 (1). doi:10.1103/physreve.77.011901. PMID 18351870. Bibcode: 2008PhRvE..77a1901R.
- Wells, W.M. III; Viola, P.; Atsumi, H.; Nakajima, S.; Kikinis, R. (1996). "Multi-modal volume registration by maximization of mutual information". Medical Image Analysis 1 (1): 35–51. doi:10.1016/S1361-8415(01)80004-9. PMID 9873920. http://www.ai.mit.edu/people/sw/papers/mia.pdf. Retrieved 2010-08-05.
- Pandey, Biswajit; Sarkar, Suman (2017). "How much a galaxy knows about its large-scale environment?: An information theoretic perspective". Monthly Notices of the Royal Astronomical Society Letters 467 (1): L6. doi:10.1093/mnrasl/slw250. Bibcode: 2017MNRAS.467L...6P.
- Janssen, Joseph; Guan, Vincent; Robeva, Elina (2023). "Ultra-marginal Feature Importance: Learning from Data with Causal Guarantees". International Conference on Artificial Intelligence and Statistics: 10782–10814. https://proceedings.mlr.press/v206/janssen23a.html.
 |
