Spherical cap

Short description: Section of a sphere

File:Spherical cap diagram.tiff

In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball cut off by a plane. It is also a spherical segment of one base, i.e., bounded by a single plane. If the plane passes through the center of the sphere (forming a great circle), so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a hemisphere.

Volume and surface area

The volume of the spherical cap and the area of the curved surface may be calculated using combinations of

• The radius [math]\displaystyle{ r }[/math] of the sphere
• The radius [math]\displaystyle{ a }[/math] of the base of the cap
• The height [math]\displaystyle{ h }[/math] of the cap
• The polar angle [math]\displaystyle{ \theta }[/math] between the rays from the center of the sphere to the apex of the cap (the pole) and the edge of the disk forming the base of the cap

	Using [math]\displaystyle{ r }[/math] and [math]\displaystyle{ h }[/math]	Using [math]\displaystyle{ a }[/math] and [math]\displaystyle{ h }[/math]	Using [math]\displaystyle{ r }[/math] and [math]\displaystyle{ \theta }[/math]
Volume	[math]\displaystyle{ V = \frac {\pi h^2}{3} (3r-h) }[/math]	[math]\displaystyle{ V = \frac{1}{6}\pi h (3a^2 + h^2) }[/math]	[math]\displaystyle{ V = \frac{\pi}{3} r^3 (2+\cos\theta) (1-\cos\theta)^2 }[/math]
Area	[math]\displaystyle{ A = 2 \pi r h }[/math]	[math]\displaystyle{ A =\pi (a^2 + h^2) }[/math]	[math]\displaystyle{ A=2 \pi r^2 (1-\cos \theta) }[/math]

If [math]\displaystyle{ \phi }[/math] denotes the latitude in geographic coordinates, then [math]\displaystyle{ \theta+\phi = \pi/2 = 90^\circ\, }[/math], and [math]\displaystyle{ \cos \theta = \sin \phi }[/math].

The relationship between [math]\displaystyle{ h }[/math] and [math]\displaystyle{ r }[/math] is relevant as long as [math]\displaystyle{ 0\le h\le2r }[/math]. For example, the red section of the illustration is also a spherical cap for which [math]\displaystyle{ h \gt r }[/math].

The formulas using [math]\displaystyle{ r }[/math] and [math]\displaystyle{ h }[/math] can be rewritten to use the radius [math]\displaystyle{ a }[/math] of the base of the cap instead of [math]\displaystyle{ r }[/math], using the Pythagorean theorem:

[math]\displaystyle{ r^2 = (r-h)^2 + a^2 = r^2 + h^2 - 2rh + a^2\,, }[/math]

so that

[math]\displaystyle{ r= \frac{a^2 + h^2}{2h}\,. }[/math]

Substituting this into the formulas gives:

[math]\displaystyle{ V = \frac {\pi h^2}{3} \left(\frac{3a^2 + 3h^2}{2h}-h \right) = \frac{1}{6}\pi h (3a^2 + h^2)\,, }[/math]

[math]\displaystyle{ A = 2 \pi \frac{(a^2 + h^2)}{2h} h = \pi (a^2 + h^2)\,. }[/math]

Deriving the surface area intuitively from the spherical sector volume

Note that aside from the calculus based argument below, the area of the spherical cap may be derived from the volume [math]\displaystyle{ V_{sec} }[/math] of the spherical sector, by an intuitive argument, as

[math]\displaystyle{ A = \frac{3}{r}V_{sec} = \frac{3}{r} \frac{2\pi r^2h}{3} = 2\pi rh\,. }[/math]

The intuitive argument is based upon summing the total sector volume from that of infinitesimal triangular pyramids. Utilizing the pyramid (or cone) volume formula of [math]\displaystyle{ V = \frac{1}{3} bh' }[/math], where [math]\displaystyle{ b }[/math] is the infinitesimal area of each pyramidal base (located on the surface of the sphere) and [math]\displaystyle{ h' }[/math] is the height of each pyramid from its base to its apex (at the center of the sphere). Since each [math]\displaystyle{ h' }[/math], in the limit, is constant and equivalent to the radius [math]\displaystyle{ r }[/math] of the sphere, the sum of the infinitesimal pyramidal bases would equal the area of the spherical sector, and:

[math]\displaystyle{ V_{sec} = \sum{V} = \sum\frac{1}{3} bh' = \sum\frac{1}{3} br = \frac{r}{3} \sum b = \frac{r}{3} A }[/math]

Deriving the volume and surface area using calculus

Rotating the green area creates a spherical cap with height [math]\displaystyle{ h }[/math] and sphere radius [math]\displaystyle{ r }[/math].

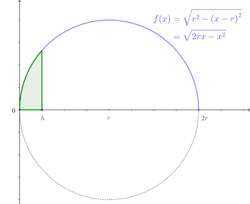
The volume and area formulas may be derived by examining the rotation of the function

[math]\displaystyle{ f(x)=\sqrt{r^2-(x-r)^2}=\sqrt{2rx-x^2} }[/math]

for [math]\displaystyle{ x \in [0,h] }[/math], using the formulas the surface of the rotation for the area and the solid of the revolution for the volume. The area is

[math]\displaystyle{ A = 2\pi\int_0^h f(x) \sqrt{1+f'(x)^2} \,dx }[/math]

The derivative of [math]\displaystyle{ f }[/math] is

[math]\displaystyle{ f'(x) = \frac{r-x}{\sqrt{2rx-x^2}} }[/math]

and hence

[math]\displaystyle{ 1+f'(x)^2 = \frac{r^2}{2rx-x^2} }[/math]

The formula for the area is therefore

[math]\displaystyle{ A = 2\pi\int_0^h \sqrt{2rx-x^2} \sqrt{\frac{r^2}{2rx-x^2}} \,dx = 2\pi \int_0^h r\,dx = 2\pi r \left[x\right]_0^h = 2 \pi r h }[/math]

The volume is

[math]\displaystyle{ V = \pi \int_0^h f(x)^2 \,dx = \pi \int_0^h (2rx-x^2) \,dx = \pi \left[rx^2-\frac13x^3\right]_0^h = \frac{\pi h^2}{3} (3r - h) }[/math]

Applications

Volumes of union and intersection of two intersecting spheres

The volume of the union of two intersecting spheres of radii [math]\displaystyle{ r_1 }[/math] and [math]\displaystyle{ r_2 }[/math] is

[math]\displaystyle{ V = V^{(1)}-V^{(2)}\,, }[/math]

where

[math]\displaystyle{ V^{(1)} = \frac{4\pi}{3}r_1^3 +\frac{4\pi}{3}r_2^3 }[/math]

is the sum of the volumes of the two isolated spheres, and

[math]\displaystyle{ V^{(2)} = \frac{\pi h_1^2}{3}(3r_1-h_1)+\frac{\pi h_2^2}{3}(3r_2-h_2) }[/math]

the sum of the volumes of the two spherical caps forming their intersection. If [math]\displaystyle{ d \le r_1+r_2 }[/math] is the distance between the two sphere centers, elimination of the variables [math]\displaystyle{ h_1 }[/math] and [math]\displaystyle{ h_2 }[/math] leads to

[math]\displaystyle{ V^{(2)} = \frac{\pi}{12d}(r_1+r_2-d)^2 \left( d^2+2d(r_1+r_2)-3(r_1-r_2)^2 \right)\,. }[/math]

Volume of a spherical cap with a curved base

The volume of a spherical cap with a curved base can be calculated by considering two spheres with radii [math]\displaystyle{ r_1 }[/math] and [math]\displaystyle{ r_2 }[/math], separated by some distance [math]\displaystyle{ d }[/math], and for which their surfaces intersect at [math]\displaystyle{ x=h }[/math]. That is, the curvature of the base comes from sphere 2. The volume is thus the difference between sphere 2's cap (with height [math]\displaystyle{ (r_2-r_1)-(d-h) }[/math]) and sphere 1's cap (with height [math]\displaystyle{ h }[/math]),

[math]\displaystyle{ \begin{align} V & = \frac{\pi h^2}{3}(3r_1-h) - \frac{\pi [(r_2-r_1)-(d-h)]^2}{3}[3r_2-((r_2-r_1)-(d-h))]\,, \\ V & = \frac{\pi h^2}{3}(3r_1-h) - \frac{\pi}{3}(d-h)^3\left(\frac{r_2-r_1}{d-h}-1\right)^2\left[\frac{2r_2+r_1}{d-h}+1\right]\,. \end{align} }[/math]

This formula is valid only for configurations that satisfy [math]\displaystyle{ 0\lt d\lt r_2 }[/math] and [math]\displaystyle{ d-(r_2-r_1)\lt h\leq r_1 }[/math]. If sphere 2 is very large such that [math]\displaystyle{ r_2\gg r_1 }[/math], hence [math]\displaystyle{ d \gg h }[/math] and [math]\displaystyle{ r_2\approx d }[/math], which is the case for a spherical cap with a base that has a negligible curvature, the above equation is equal to the volume of a spherical cap with a flat base, as expected.

Areas of intersecting spheres

Consider two intersecting spheres of radii [math]\displaystyle{ r_1 }[/math] and [math]\displaystyle{ r_2 }[/math], with their centers separated by distance [math]\displaystyle{ d }[/math]. They intersect if

[math]\displaystyle{ |r_1-r_2|\leq d \leq r_1+r_2 }[/math]

From the law of cosines, the polar angle of the spherical cap on the sphere of radius [math]\displaystyle{ r_1 }[/math] is

[math]\displaystyle{ \cos \theta = \frac{r_1^2-r_2^2+d^2}{2r_1d} }[/math]

Using this, the surface area of the spherical cap on the sphere of radius [math]\displaystyle{ r_1 }[/math] is

[math]\displaystyle{ A_1 = 2\pi r_1^2 \left( 1+\frac{r_2^2-r_1^2-d^2}{2 r_1 d} \right) }[/math]

Surface area bounded by parallel disks

The curved surface area of the spherical segment bounded by two parallel disks is the difference of surface areas of their respective spherical caps. For a sphere of radius [math]\displaystyle{ r }[/math], and caps with heights [math]\displaystyle{ h_1 }[/math] and [math]\displaystyle{ h_2 }[/math], the area is

[math]\displaystyle{ A=2 \pi r |h_1 - h_2|\,, }[/math]

or, using geographic coordinates with latitudes [math]\displaystyle{ \phi_1 }[/math] and [math]\displaystyle{ \phi_2 }[/math],

[math]\displaystyle{ A=2 \pi r^2 |\sin \phi_1 - \sin \phi_2|\,, }[/math]

For example, assuming the Earth is a sphere of radius 6371 km, the surface area of the arctic (north of the Arctic Circle, at latitude 66.56° as of August 2016) is 2π·6371²|sin 90° − sin 66.56°| = 21.04 million km², or 0.5·|sin 90° − sin 66.56°| = 4.125% of the total surface area of the Earth.

This formula can also be used to demonstrate that half the surface area of the Earth lies between latitudes 30° South and 30° North in a spherical zone which encompasses all of the Tropics.

Generalizations

Sections of other solids

The spheroidal dome is obtained by sectioning off a portion of a spheroid so that the resulting dome is circularly symmetric (having an axis of rotation), and likewise the ellipsoidal dome is derived from the ellipsoid.

Hyperspherical cap

Generally, the [math]\displaystyle{ n }[/math]-dimensional volume of a hyperspherical cap of height [math]\displaystyle{ h }[/math] and radius [math]\displaystyle{ r }[/math] in [math]\displaystyle{ n }[/math]-dimensional Euclidean space is given by: [math]\displaystyle{ V = \frac{\pi ^ {\frac{n-1}{2}}\, r^{n}}{\,\Gamma \left ( \frac{n+1}{2} \right )} \int_{0}^{\arccos\left(\frac{r-h}{r}\right)}\sin^n (\theta) \,\mathrm{d}\theta }[/math] where [math]\displaystyle{ \Gamma }[/math] (the gamma function) is given by [math]\displaystyle{ \Gamma(z) = \int_0^\infty t^{z-1} \mathrm{e}^{-t}\,\mathrm{d}t }[/math].

The formula for [math]\displaystyle{ V }[/math] can be expressed in terms of the volume of the unit n-ball [math]\displaystyle{ C_n = \pi^{n/2} / \Gamma[1+\frac{n}{2}] }[/math] and the hypergeometric function [math]\displaystyle{ {}_{2}F_{1} }[/math] or the regularized incomplete beta function [math]\displaystyle{ I_x(a,b) }[/math] as [math]\displaystyle{ V = C_{n} \, r^{n} \left( \frac{1}{2}\, - \,\frac{r-h}{r} \,\frac{\Gamma[1+\frac{n}{2}]}{\sqrt{\pi}\,\Gamma[\frac{n+1}{2}]} {\,\,}_{2}F_{1}\left(\tfrac{1}{2},\tfrac{1-n}{2};\tfrac{3}{2};\left(\tfrac{r-h}{r}\right)^{2}\right)\right) = \frac{1}{2}C_{n} \, r^n I_{(2rh-h^2)/r^2} \left(\frac{n+1}{2}, \frac{1}{2} \right), }[/math]

and the area formula [math]\displaystyle{ A }[/math] can be expressed in terms of the area of the unit n-ball [math]\displaystyle{ A_{n}={\scriptstyle 2\pi^{n/2}/\Gamma[\frac{n}{2}]} }[/math] as [math]\displaystyle{ A =\frac{1}{2}A_{n} \, r^{n-1} I_{(2rh-h^2)/r^2} \left(\frac{n-1}{2}, \frac{1}{2} \right), }[/math] where [math]\displaystyle{ 0\le h\le r }[/math].

Earlier in (1986, USSR Academ. Press) the following formulas were derived: [math]\displaystyle{ A = A_n p_ { n-2 } (q), V = C_n p_n (q) , }[/math] where [math]\displaystyle{ q = 1-h/r (0 \le q \le 1 ), p_n (q) =(1-G_n(q)/G_n(1))/2 , }[/math] [math]\displaystyle{ G _n(q)= \int _0^q (1-t^2) ^ { (n-1) /2 } dt . }[/math]

For odd [math]\displaystyle{ n=2k+1 }[/math]: [math]\displaystyle{ G_n(q) = \sum_{i=0}^k (-1) ^i \binom k i \frac {q^{2i+1}} {2i+1} . }[/math]

Asymptotics

It is shown in that, if [math]\displaystyle{ n \to \infty }[/math] and [math]\displaystyle{ q\sqrt n = \text{const.} }[/math], then [math]\displaystyle{ p_n (q) \to 1- F({q \sqrt n}) }[/math] where [math]\displaystyle{ F() }[/math] is the integral of the standard normal distribution.

A more quantitative bound is [math]\displaystyle{ A/A_n = n^{\Theta(1)} \cdot [(2-h/r)h/r]^{n/2} }[/math]. For large caps (that is when [math]\displaystyle{ (1-h/r)^4\cdot n = O(1) }[/math] as [math]\displaystyle{ n\to \infty }[/math]), the bound simplifies to [math]\displaystyle{ n^{\Theta(1)} \cdot e^{-(1-h/r)^2n/2} }[/math].

See also

• Circular segment — the analogous 2D object
• Solid angle — contains formula for n-sphere caps
• Spherical segment
• Spherical sector
• Spherical wedge

Further reading

• Richmond, Timothy J. (1984). "Solvent accessible surface area and excluded volume in proteins: Analytical equation for overlapping spheres and implications for the hydrophobic effect". Journal of Molecular Biology 178 (1): 63–89. doi:10.1016/0022-2836(84)90231-6. PMID 6548264. 
• Lustig, Rolf (1986). "Geometry of four hard fused spheres in an arbitrary spatial configuration". Molecular Physics 59 (2): 195–207. doi:10.1080/00268978600102011. Bibcode: 1986MolPh..59..195L. 
• Gibson, K. D.; Scheraga, Harold A. (1987). "Volume of the intersection of three spheres of unequal size: a simplified formula". The Journal of Physical Chemistry 91 (15): 4121–4122. doi:10.1021/j100299a035. 
• Gibson, K. D.; Scheraga, Harold A. (1987). "Exact calculation of the volume and surface area of fused hard-sphere molecules with unequal atomic radii". Molecular Physics 62 (5): 1247–1265. doi:10.1080/00268978700102951. Bibcode: 1987MolPh..62.1247G. 
• Petitjean, Michel (1994). "On the analytical calculation of van der Waals surfaces and volumes: some numerical aspects". Journal of Computational Chemistry 15 (5): 507–523. doi:10.1002/jcc.540150504. 
• Grant, J. A.; Pickup, B. T. (1995). "A Gaussian description of molecular shape". The Journal of Physical Chemistry 99 (11): 3503–3510. doi:10.1021/j100011a016. 
• Busa, Jan; Dzurina, Jozef; Hayryan, Edik; Hayryan, Shura (2005). "ARVO: A fortran package for computing the solvent accessible surface area and the excluded volume of overlapping spheres via analytic equations". Computer Physics Communications 165 (1): 59–96. doi:10.1016/j.cpc.2004.08.002. Bibcode: 2005CoPhC.165...59B. 

External links

• Weisstein, Eric W.. "Spherical cap". http://mathworld.wolfram.com/SphericalCap.html.  Derivation and some additional formulas.
• Online calculator for spherical cap volume and area.
• Summary of spherical formulas.