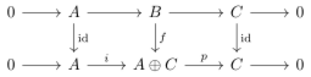Split exact sequence

In mathematics, a split exact sequence is a short exact sequence in which the middle term is built out of the two outer terms in the simplest possible way.

Equivalent characterizations

A short exact sequence of abelian groups or of modules over a fixed ring, or more generally of objects in an abelian category

[math]\displaystyle{ 0 \to A \mathrel{\stackrel{a}{\to}} B \mathrel{\stackrel{b}{\to}} C \to 0 }[/math]

is called split exact if it is isomorphic to the exact sequence where the middle term is the direct sum of the outer ones:

[math]\displaystyle{ 0 \to A \mathrel{\stackrel{i}{\to}} A \oplus C \mathrel{\stackrel{p}{\to}} C \to 0 }[/math]

The requirement that the sequence is isomorphic means that there is an isomorphism [math]\displaystyle{ f : B \to A \oplus C }[/math] such that the composite [math]\displaystyle{ f \circ a }[/math] is the natural inclusion [math]\displaystyle{ i: A \to A \oplus C }[/math] and such that the composite [math]\displaystyle{ p \circ f }[/math] equals b. This can be summarized by a commutative diagram as:

The splitting lemma provides further equivalent characterizations of split exact sequences.

Examples

A trivial example of a split short exact sequence is

[math]\displaystyle{ 0 \to M_1 \mathrel{\stackrel{q}{\to}} M_1\oplus M_2 \mathrel{\stackrel{p}{\to}} M_2 \to 0 }[/math]

where [math]\displaystyle{ M_1, M_2 }[/math] are R-modules, [math]\displaystyle{ q }[/math] is the canonical injection and [math]\displaystyle{ p }[/math] is the canonical projection.

Any short exact sequence of vector spaces is split exact. This is a rephrasing of the fact that any set of linearly independent vectors in a vector space can be extended to a basis.

The exact sequence [math]\displaystyle{ 0 \to \mathbf{Z}\mathrel{\stackrel{2}{\to}} \mathbf{Z}\to \mathbf{Z}/ 2 \to 0 }[/math] (where the first map is multiplication by 2) is not split exact.

Related notions

Pure exact sequences can be characterized as the filtered colimits of split exact sequences.

Sources

• Fuchs, László (2015), Abelian Groups, Springer Monographs in Mathematics, Springer, ISBN 9783319194226 
• Sharp, R. Y., Rodney (2001), Steps in Commutative Algebra, 2nd ed., London Mathematical Society Student Texts, Cambridge University Press, ISBN 0521646235