Steiner inellipse

Short description: Unique ellipse tangent to all 3 midpoints of a given triangle's sides

The Steiner Inellipse. According to Marden's theorem, given the triangle with vertices (1, 7), (7, 5), (3, 1), the foci of the inellipse are (3, 5) and (13/3, 11/3), since [math]\displaystyle{ \begin{align} & D_x(1+7i-x)(7+5i-x)(3+i-x) \\ & = -3\left(\tfrac{13}{3}+\tfrac{11}{3}i-x\right)(3+5i-x) \end{align} }[/math]

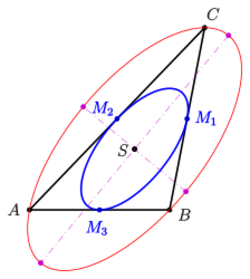
In geometry, the Steiner inellipse, midpoint inellipse, or midpoint ellipse of a triangle is the unique ellipse inscribed in the triangle and tangent to the sides at their midpoints. It is an example of an inellipse. By comparison the inscribed circle and Mandart inellipse of a triangle are other inconics that are tangent to the sides, but not at the midpoints unless the triangle is equilateral. The Steiner inellipse is attributed by Dörrie to Jakob Steiner, and a proof of its uniqueness is given by Dan Kalman.

The Steiner inellipse contrasts with the Steiner circumellipse, also called simply the Steiner ellipse, which is the unique ellipse that passes through the vertices of a given triangle and whose center is the triangle's centroid.

Definition and properties

Definition

An ellipse that is tangent to the sides of a triangle △ABC at its midpoints [math]\displaystyle{ M_1,M_2,M_3 }[/math] is called the Steiner inellipse of △ABC.

  Arbitrary triangle △ABC

  Steiner inellipse

  Steiner ellipse

  Major and minor axes

  Equilateral triangle △ABC

  Steiner inellipse

  Steiner ellipse

Properties:
For an arbitrary triangle △ABC with midpoints [math]\displaystyle{ M_1,M_2,M_3 }[/math] of its sides the following statements are true:
a) There exists exactly one Steiner inellipse.
b) The center of the Steiner inellipse is the centroid S of △ABC.
c1) The triangle [math]\displaystyle{ \triangle M_1M_2M_3 }[/math] has the same centroid S and the Steiner inellipse of △ABC is the Steiner ellipse of the triangle [math]\displaystyle{ \triangle M_1M_2M_3. }[/math]
c2) The Steiner inellipse of a triangle is the scaled Steiner Ellipse with scaling factor 1/2 and the centroid as center. Hence both ellipses have the same eccentricity, are similar.
d) The area of the Steiner inellipse is [math]\displaystyle{ \tfrac{\pi}{3 \sqrt{3}} }[/math]-times the area of the triangle.
e) The Steiner inellipse has the greatest area of all inellipses of the triangle.

Proof

The proofs of properties a),b),c) are based on the following properties of an affine mapping: 1) any triangle can be considered as an affine image of an equilateral triangle. 2) Midpoints of sides are mapped onto midpoints and centroids on centroids. The center of an ellipse is mapped onto the center of its image.
Hence its suffice to prove properties a),b),c) for an equilateral triangle:
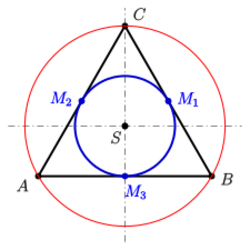
a) To any equilateral triangle there exists an incircle. It touches the sides at its midpoints. There is no other (non-degenerate) conic section with the same properties, because a conic section is determined by 5 points/tangents.
b) By a simple calculation.
c) The circumcircle is mapped by a scaling, with factor 1/2 and the centroid as center, onto the incircle. The eccentricity is an invariant.
d) The ratio of areas is invariant to affine transformations. So the ratio can be calculated for the equilateral triangle.
e) See Inellipse.

Parametric representation and semi-axes

Parametric representation:

• Because a Steiner inellipse of a triangle △ABC is a scaled Steiner ellipse (factor 1/2, center is centroid) one gets a parametric representation derived from the trigonometric representation of the Steiner ellipse :

[math]\displaystyle{ \vec x =\vec p(t)=\overrightarrow{OS}\; +\; {\color{blue}\frac 1 2 }\overrightarrow{SC}\; \cos t \;+\; \frac{1}{{\color{blue}2}\sqrt{3}}\overrightarrow{AB}\; \sin t \; , \quad 0\le t \lt 2\pi\ . }[/math]

• The 4 vertices of the Steiner inellipse are

[math]\displaystyle{ \vec p(t_0),\; \vec p(t_0\pm\frac{\pi}{2}),\; \vec p(t_0+\pi), }[/math]

where t₀ is the solution of

[math]\displaystyle{ \cot (2t_0)= \tfrac{\vec f_1^{\, 2}-\vec f_2^{\, 2}}{2\vec f_1 \cdot \vec f_2}\quad }[/math] with [math]\displaystyle{ \quad \vec f_1=\frac 1 2 \vec{SC},\quad \vec f_2=\frac{1}{2\sqrt{3}}\vec{AB}\ . }[/math]

Semi-axes:

• With the abbreviations

[math]\displaystyle{ \begin{align} M &:= {\color{blue} \frac 1 4} \left(\vec{SC}^2+\frac{1}{3}\vec{AB}^2 \right) \\ N &:= \frac{1}{{\color{blue}4}\sqrt{3}} \left|\det \left(\vec{SC},\vec{AB} \right)\right| \end{align} }[/math]

one gets for the semi-axes a, b (where a > b):

[math]\displaystyle{ \begin{align} a &= \frac{1}{2} \left(\sqrt{M+2N}+\sqrt{M-2N} \right) \\ b &= \frac{1}{2} \left(\sqrt{M+2N}-\sqrt{M-2N} \right)\ . \end{align} }[/math]

• The linear eccentricity c of the Steiner inellipse is

[math]\displaystyle{ c=\sqrt{a^2-b^2}=\dotsb=\sqrt{\sqrt{M^2-4N^2}}\ . }[/math]

Trilinear equation

The equation of the Steiner inellipse in trilinear coordinates for a triangle with side lengths a, b, c (with these parameters having a different meaning than previously) is

[math]\displaystyle{ a^2x^2+b^2y^2+c^2z^2-2abxy-2bcyz-2cazx = 0 }[/math]

where x is an arbitrary positive constant times the distance of a point from the side of length a, and similarly for b and c with the same multiplicative constant.

Other properties

The lengths of the semi-major and semi-minor axes for a triangle with sides a, b, c are

[math]\displaystyle{ \frac{1}{6}\sqrt{a^2+b^2+c^2 \pm 2Z}, }[/math]

where

[math]\displaystyle{ Z=\sqrt{a^4+b^4+c^4-a^2b^2-b^2c^2-c^2a^2}. }[/math]

According to Marden's theorem, if the three vertices of the triangle are the complex zeros of a cubic polynomial, then the foci of the Steiner inellipse are the zeros of the derivative of the polynomial.

The major axis of the Steiner inellipse is the line of best orthogonal fit for the vertices.

Denote the centroid and the first and second Fermat points of a triangle as [math]\displaystyle{ G,F_+,F_- }[/math] respectively. The major axis of the triangle's Steiner inellipse is the inner bisector of [math]\displaystyle{ \angle F_+GF_-. }[/math] The lengths of the axes are [math]\displaystyle{ |GF_-| \pm |GF_+|\! ; }[/math] that is, the sum and difference of the distances of the Fermat points from the centroid.

The axes of the Steiner inellipse of a triangle are tangent to its Kiepert parabola, the unique parabola that is tangent to the sides of the triangle and has the Euler line as its directrix.

The foci of the Steiner inellipse of a triangle are the intersections of the inellipse's major axis and the circle with center on the minor axis and going through the Fermat points.

As with any ellipse inscribed in a triangle △ABC, letting the foci be P and Q we have

[math]\displaystyle{ \frac{\overline{PA} \cdot \overline{QA}}{\overline{CA} \cdot \overline{AB}} + \frac{\overline{PB} \cdot \overline{QB}}{\overline{AB} \cdot \overline{BC}} + \frac{\overline{PC} \cdot \overline{QC}}{\overline{BC} \cdot \overline{CA}} = 1. }[/math]

Generalization

The Steiner inellipse of a triangle can be generalized to n-gons: some n-gons have an interior ellipse that is tangent to each side at the side's midpoint. Marden's theorem still applies: the foci of the Steiner inellipse are zeroes of the derivative of the polynomial whose zeroes are the vertices of the n-gon.