Three-gap theorem

From HandWiki
Short description: On distances between points on a circle

In mathematics, the three-gap theorem, three-distance theorem, or Steinhaus conjecture states that if one places n points on a circle, at angles of θ, 2θ, 3θ, ... from the starting point, then there will be at most three distinct distances between pairs of points in adjacent positions around the circle. When there are three distances, the largest of the three always equals the sum of the other two.[1] Unless θ is a rational multiple of π, there will also be at least two distinct distances.

This result was conjectured by Hugo Steinhaus, and proved in the 1950s by Vera T. Sós, János Surányi (hu), and Stanisław Świerczkowski; more proofs were added by others later. Applications of the three-gap theorem include the study of plant growth and musical tuning systems, and the theory of light reflection within a mirrored square.

Statement

The three-gap theorem can be stated geometrically in terms of points on a circle. In this form, it states that if one places [math]\displaystyle{ n }[/math] points on a circle, at angles of [math]\displaystyle{ \theta, 2\theta, \dots, n\theta }[/math] from the starting point, then there will be at most three distinct distances between pairs of points in adjacent positions around the circle. An equivalent and more algebraic form involves the fractional parts of multiples of a real number. It states that, for any positive real number [math]\displaystyle{ \alpha }[/math] and integer [math]\displaystyle{ n }[/math], the fractional parts of the numbers [math]\displaystyle{ \alpha, 2\alpha, \dots, n\alpha }[/math] divide the unit interval into subintervals with at most three different lengths. The two problems are equivalent under a linear correspondence between the unit interval and the circumference of the circle, and a correspondence between the real number [math]\displaystyle{ \alpha }[/math] and the angle [math]\displaystyle{ \theta=2\pi\alpha }[/math].[2][3][4]

Applications

Plant growth

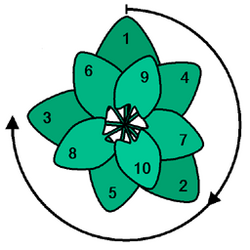
End-on view of a plant stem in which consecutive leaves are separated by the golden angle

In the study of phyllotaxis, the arrangements of leaves on plant stems, it has been observed that each successive leaf on the stems of many plants is turned from the previous leaf by the golden angle, approximately 137.5°. It has been suggested that this angle maximizes the sun-collecting power of the plant's leaves.[5] If one looks end-on at a plant stem that has grown in this way, there will be at most three distinct angles between two leaves that are consecutive in the cyclic order given by this end-on view.[6]

Points spaced at the golden angle along a Fermat spiral (center) are more uniformly spaced than for other angles.

For example, in the figure, the largest of these three angles occurs three times, between the leaves numbered 3 and 6, between leaves 4 and 7, and between leaves 5 and 8. The second-largest angle occurs five times, between leaves 6 and 1, 9 and 4, 7 and 2, 10 and 5, and 8 and 3. And the smallest angle occurs only twice, between leaves 1 and 9 and between leaves 2 and 10. The phenomenon of having three types of distinct gaps depends only on fact that the growth pattern uses a constant rotation angle, and not on the relation of this angle to the golden ratio; the same phenomenon would happen for any other rotation angle, and not just for the golden angle. However, other properties of this growth pattern do depend on the golden ratio. For instance, the fact that golden ratio is a badly approximable number implies that points spaced at this angle along the Fermat spiral (as they are in some models of plant growth) form a Delone set; intuitively, this means that they are uniformly spaced.[7]

Music theory

Tones of the Pythagorean tuning as points of the chromatic circle. Edges indicate the perfect fifths used to construct the tuning; the two longer gap lengths between consecutive points represent semitones, and the short gap where the dodecagram fails to close up is the Pythagorean comma.

In music theory, a musical interval describes the ratio in frequency between two musical tones. Intervals are commonly considered consonant or harmonious when they are the ratio of two small integers; for instance, the octave corresponds to the ratio 2:1, while the perfect fifth corresponds to the ratio 3:2.[8] Two tones are commonly considered to be equivalent when they differ by a whole number of octaves; this equivalence can be represented geometrically by the chromatic circle, the points of which represent classes of equivalent tones. Mathematically, this circle can be described as the unit circle in the complex plane, and the point on this circle that represents a given tone can be obtained by the mapping the frequency [math]\displaystyle{ \nu }[/math] to the complex number [math]\displaystyle{ \exp(2\pi i\log_2\nu) }[/math]. An interval with ratio [math]\displaystyle{ \rho }[/math] corresponds to the angle [math]\displaystyle{ 2\pi\log_2\rho }[/math] between points on this circle, meaning that two musical tones differ by the given interval when their two points on the circle differ by this angle. For instance, this formula gives [math]\displaystyle{ 2\pi }[/math] (a whole circle) as the angle corresponding to an octave. Because 3/2 is not a rational power of two, the angle on the chromatic circle that represents a perfect fifth is not a rational multiple of [math]\displaystyle{ 2\pi }[/math], and similarly other common musical intervals other than the octave do not correspond to rational angles.[9]

A tuning system is a collection of tones used to compose and play music. For instance, the equal temperament commonly used for the piano is a tuning system, consisting of 12 tones equally spaced around the chromatic circle. Some other tuning systems do not space their tones equally, but instead generate them by some number of consecutive multiples of a given interval. An example is the Pythagorean tuning, which is constructed in this way from twelve tones, generated as the consecutive multiples of a perfect fifth in the circle of fifths. The irrational angle formed on the chromatic circle by a perfect fifth is close to 7/12 of a circle, and therefore the twelve tones of the Pythagorean tuning are close to, but not the same as, the twelve tones of equal temperament, which could be generated in the same way using an angle of exactly 7/12 of a circle.[10] Instead of being spaced at angles of exactly 1/12 of a circle, as the tones of equal temperament would be, the tones of the Pythagorean tuning are separated by intervals of two different angles, close to but not exactly 1/12 of a circle, representing two different types of semitones.[11] If the Pythagorean tuning system were extended by one more perfect fifth, to a set of 13 tones, then the sequence of intervals between its tones would include a third, much shorter interval, the Pythagorean comma.[12]

In this context, the three-gap theorem can be used to describe any tuning system that is generated in this way by consecutive multiples of a single interval. Some of these tuning systems (like equal temperament) may have only one interval separating the closest pairs of tones, and some (like the Pythagorean tuning) may have only two different intervals separating the tones, but the three-gap theorem implies that there are always at most three different intervals separating the tones.[13][14]

Mirrored reflection

In the Fibonacci word, an example of a Sturmian word, there are four distinct length-3 subsequences (in left-right order): 010, 100, 001, and 101.

A Sturmian word is infinite sequences of two symbols (for instance, "H" and "V") describing the sequence of horizontal and vertical reflections of a light ray within a mirrored square, starting along a line of irrational slope. Equivalently, the same sequence describes the sequence of horizontal and vertical lines of the integer grid that are crossed by the starting line. One property that all such sequences have is that, for any positive integer n, the sequence has exactly n + 1 distinct consecutive subsequences of length n. Each subsequence occurs infinitely often with a certain frequency, and the three-gap theorem implies that these n + 1 subsequences occur with at most three distinct frequencies. If there are three frequencies, then the largest frequency must equal the sum of the other two. One proof of this result involves partitioning the y-intercepts of the starting lines (modulo 1) into n + 1 subintervals within which the initial n elements of the sequence are the same, and applying the three-gap theorem to this partition.[15][16]

History and proof

The three-gap theorem was conjectured by Hugo Steinhaus, and its first[17] proofs were found in the late 1950s by Vera T. Sós,[18] János Surányi (hu),[19] and Stanisław Świerczkowski.[20] Later researchers published additional proofs,[21] generalizing this result to higher dimensions[22][23][24][25], and connecting it to topics including continued fractions,[4][26] symmetries and geodesics of Riemannian manifolds,[27] ergodic theory,[28] and the space of planar lattices.[3] (Mayero 2000) formalizes a proof using the Coq interactive theorem prover.[2]

The following simple proof is due to Frank Liang. Let θ be the rotation angle generating a set of points as some number of consecutive multiples of θ on a circle. Define a gap to be an arc A of the circle that extends between two adjacent points of the given set, and define a gap to be rigid if its endpoints occur later in the sequence of multiples of θ than any other gap of the same length. From this definition, it follows that every gap has the same length as a rigid gap. If A is a rigid gap, then A + θ is not a gap, because it has the same length and would be one step later. The only ways for this to happen are for one of the endpoints of A to be the last point in the sequence of multiples of θ (so that the corresponding endpoint of A + θ is missing) or for one of the given points to land within A + θ, preventing it from being a gap. A point can only land within A + θ if it is the first point in the sequence of multiples of θ, because otherwise its predecessor in the sequence would land within A, contradicting the assumption that A is a gap. So there can be at most three rigid gaps, the two on either side of the last point and the one in which the predecessor of the first point (if it were part of the sequence) would land. Because there are at most three rigid gaps, there are at most three lengths of gaps.[29][30]

Related results

Liang's proof additionally shows that, when there are exactly three gap lengths, the longest gap length is the sum of the other two. For, in this case, the rotated copy A + θ that has the first point in it is partitioned by that point into two smaller gaps, which must be the other two gaps.[29][30] Liang also proves a more general result, the "[math]\displaystyle{ 3d }[/math] distance theorem", according to which the union of [math]\displaystyle{ d }[/math] different arithmetic progressions on a circle has at most [math]\displaystyle{ 3d }[/math] different gap lengths.[29] In the three-gap theorem, there is a constant bound on the ratios between the three gaps, if and only if θ/2π is a badly approximable number.[7]

A closely related but earlier theorem, also called the three-gap theorem, is that if A is any arc of the circle, then the integer sequence of multiples of θ that land in A has at most three lengths of gaps between sequence values. Again, if there are three gap lengths then one is the sum of the other two.[31][32]

See also

References

  1. ↑ Allouche, Jean-Paul; Shallit, Jeffrey (2003), "2.6 The Three-Distance Theorem", Automatic Sequences: Theory, Applications, Generalizations, Cambridge University Press, pp. 53–55, ISBN 9780521823326, https://books.google.com/books?id=2ZsSUStt96sC&pg=PA53 
  2. ↑ 2.0 2.1 Mayero, Micaela (2000), "The three gap theorem (Steinhaus conjecture)", Types for Proofs and Programs: International Workshop, TYPES'99, Lökeberg, Sweden, June 12–16, 1999, Selected Papers, Lecture Notes in Computer Science, 1956, Springer, pp. 162–173, doi:10.1007/3-540-44557-9_10, ISBN 978-3-540-41517-6 
  3. ↑ 3.0 3.1 Marklof, Jens; Strömbergsson, Andreas (2017), "The three gap theorem and the space of lattices", The American Mathematical Monthly 124 (8): 741–745, doi:10.4169/amer.math.monthly.124.8.741 
  4. ↑ 4.0 4.1 van Ravenstein, Tony (1988), "The three-gap theorem (Steinhaus conjecture)", Journal of the Australian Mathematical Society, Series A 45 (3): 360–370, doi:10.1017/S1446788700031062 
  5. ↑ Adam, John A. (2011), A Mathematical Nature Walk, Princeton University Press, pp. 35–41, ISBN 9781400832903, https://books.google.com/books?id=5ou-E9UKS_AC&pg=PA35 
  6. ↑ van Ravenstein, Tony (1987), "Number sequences and phyllotaxis", Bulletin of the Australian Mathematical Society 36 (2): 333, doi:10.1017/s0004972700026605 
  7. ↑ 7.0 7.1 Akiyama, Shigeki (March 2020), "Spiral Delone sets and three distance theorem", Nonlinearity 33 (5): 2533–2540, doi:10.1088/1361-6544/ab74ad, Bibcode: 2020Nonli..33.2533A 
  8. ↑ Haack, Joel K. (1999), "The mathematics of the just intonation used in the music of Terry Riley", in Sarhangi, Reza, Bridges: Mathematical Connections in Art, Music, and Science, Southwestern College, Winfield, Kansas: Bridges Conference, pp. 101–110, ISBN 0-9665201-1-4, https://archive.bridgesmathart.org/1999/bridges1999-101.html 
  9. ↑ Baroin, Gilles; Calvet, André (2019), "Visualizing temperaments: squaring the circle?", in Montiel, Mariana; Gomez-Martin, Francisco; Agustín-Aquino, Octavio A., Mathematics and Computation in Music: 7th International Conference, MCM 2019, Madrid, Spain, June 18–21, 2019, Proceedings, Springer International Publishing, pp. 333–337, doi:10.1007/978-3-030-21392-3_27 
  10. ↑ Carey, Norman; Clampitt, David (October 1989), "Aspects of well-formed scales", Music Theory Spectrum 11 (2): 187–206, doi:10.2307/745935 
  11. ↑ Strohm, Reinhard; Blackburn, Bonnie J., eds. (2001), Music as Concept and Practice in the Late Middle Ages, Volume 3, Part 1, New Oxford history of music, Oxford University Press, p. 252, ISBN 9780198162056, https://books.google.com/books?id=tR11H5BHT0EC&pg=PA252 
  12. ↑ Benson, Donald C. (2003), A Smoother Pebble: Mathematical Explorations, Oxford University Press, p. 51, ISBN 9780198032977, https://books.google.com/books?id=nXZJauwH2N0C&pg=PA51 
  13. ↑ Carey, Norman (2007), "Coherence and sameness in well-formed and pairwise well-formed scales", Journal of Mathematics and Music 1 (2): 79–98, doi:10.1080/17459730701376743 
  14. ↑ Narushima, Terumi (2017), Microtonality and the Tuning Systems of Erv Wilson: Mapping the Harmonic Spectrum, Routledge Studies in Music Theory, Routledge, pp. 90–91, ISBN 9781317513421, https://books.google.com/books?id=_jBEDwAAQBAJ&pg=PT90 
  15. ↑ Lothaire, M. (2002), "Sturmian Words", Algebraic Combinatorics on Words, Cambridge: Cambridge University Press, pp. 40–97, ISBN 978-0-521-81220-7, http://www-igm.univ-mlv.fr/%7Eberstel/Lothaire/ChapitresACW/C2.ps . Lothaire uses the property of having [math]\displaystyle{ d+1 }[/math] words of length [math]\displaystyle{ d }[/math] as a definition of Sturmian words, rather than as a consequence of the definition. For the equivalence of this property with the definition stated here, see Theorem 2.1.13, p. 51. For the three frequencies of these words see Theorem 2.2.37, p. 73.
  16. ↑ Alessandri, Pascal (1998), "Three distance theorems and combinatorics on words", L'Enseignement mathématique 44 (1–2): 103–132, https://www.irif.fr/~berthe/Articles/3d.ps ; see in particular Section 2.1, "Complexity and frequencies of codings of rotations"
  17. ↑ Haynes, Alan; Marklof, Jens (2020), "Higher dimensional Steinhaus and Slater problems via homogeneous dynamics", Annales Scientifiques de l'École Normale Supérieure 53 (2): 537–557, doi:10.24033/asens.2427, "The first proofs of this remarkable fact were published in 1957 by Sós, in 1958 by Surányi, and in 1959 by Świerczkowski" 
  18. ↑ "On the distribution mod 1 of the sequence [math]\displaystyle{ n\alpha }[/math]", Ann. Univ. Sci. Budapest, Eötvös Sect. Math. 1: 127–134, 1958 
  19. ↑ Surányi, J. (1958), "Über die Anordnung der Vielfachen einer reelen Zahl mod 1", Ann. Univ. Sci. Budapest, Eötvös Sect. Math. 1: 107–111 
  20. ↑ "On successive settings of an arc on the circumference of a circle", Fundamenta Mathematicae 46 (2): 187–189, 1959, doi:10.4064/fm-46-2-187-189 
  21. ↑ These proofs are briefly surveyed and classified by (Marklof Strömbergsson), from which the following classification of these proofs and many of their references are taken.
  22. ↑ Halton, John H. (1965), "The distribution of the sequence [math]\displaystyle{ \{n\xi\}\,(n=0,\,1,\,2,\,\ldots) }[/math]", Mathematical Proceedings of the Cambridge Philosophical Society 61 (3): 665–670, doi:10.1017/S0305004100039013 
  23. ↑ Chevallier, Nicolas (2007), "Cyclic groups and the three distance theorem", Canadian Journal of Mathematics 59 (3): 503–552, doi:10.4153/CJM-2007-022-3 
  24. ↑ Vijay, Sujith (2008), "Eleven Euclidean distances are enough", Journal of Number Theory 128 (6): 1655–1661, doi:10.1016/j.jnt.2007.08.016 
  25. ↑ Bleher, Pavel M.; Homma, Youkow; Ji, Lyndon L.; Roeder, Roland K. W.; Shen, Jeffrey D. (2012), "Nearest neighbor distances on a circle: multidimensional case", Journal of Statistical Physics 146 (2): 446–465, doi:10.1007/s10955-011-0367-8, Bibcode: 2012JSP...146..446B 
  26. ↑ Slater, Noel B. (1967), "Gaps and steps for the sequence [math]\displaystyle{ n\theta \bmod 1 }[/math]", Mathematical Proceedings of the Cambridge Philosophical Society 63 (4): 1115–1123, doi:10.1017/S0305004100042195 
  27. ↑ Biringer, Ian; Schmidt, Benjamin (2008), "The three gap theorem and Riemannian geometry", Geometriae Dedicata 136: 175–190, doi:10.1007/s10711-008-9283-8 
  28. ↑ Haynes, Alan; Koivusalo, Henna; Walton, James; Sadun, Lorenzo (2016), "Gaps problems and frequencies of patches in cut and project sets", Mathematical Proceedings of the Cambridge Philosophical Society 161 (1): 65–85, doi:10.1017/S0305004116000128, Bibcode: 2016MPCPS.161...65H, http://dro.dur.ac.uk/22176/1/22176.pdf 
  29. ↑ 29.0 29.1 29.2 Liang, Frank M. (1979), "A short proof of the [math]\displaystyle{ 3d }[/math] distance theorem", Discrete Mathematics 28 (3): 325–326, doi:10.1016/0012-365X(79)90140-7 
  30. ↑ 30.0 30.1 Shiu, Peter (2018), "A footnote to the three gaps theorem", The American Mathematical Monthly 125 (3): 264–266, doi:10.1080/00029890.2018.1412210 
  31. ↑ Slater, N. B. (1950), "The distribution of the integers [math]\displaystyle{ N }[/math] for which [math]\displaystyle{ \theta N\lt \phi }[/math]", Mathematical Proceedings of the Cambridge Philosophical Society 46 (4): 525–534, doi:10.1017/S0305004100026086 
  32. ↑ Florek, K. (1951), "Une remarque sur la répartition des nombres [math]\displaystyle{ n\xi\, (\operatorname{mod} 1) }[/math]", Colloquium Mathematicum 2: 323–324 



Retrieved from "https://handwiki.org/wiki/index.php?title=Three-gap_theorem&oldid=3359576"