Dodecagram

Short description: Star polygon with 12 vertices

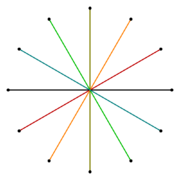
In geometry, a dodecagram (from el δώδεκα (dṓdeka) 'twelve', and γραμμῆς (grammēs) 'line') is a star polygon or compound with 12 vertices. There is one regular dodecagram polygon (with Schläfli symbol {12/5} and a turning number of 5). There are also 4 regular compounds {12/2}, {12/3}, {12/4}, and {12/6}.

Regular dodecagram

There is one regular form: {12/5}, containing 12 vertices, with a turning number of 5. A regular dodecagram has the same vertex arrangement as a regular dodecagon, which may be regarded as {12/1}.

Dodecagrams as regular compounds

There are four regular dodecagram star figures: {12/2}=2{6}, {12/3}=3{4}, {12/4}=4{3}, and {12/6}=6{2}. The first is a compound of two hexagons, the second is a compound of three squares, the third is a compound of four triangles, and the fourth is a compound of six straight-sided digons. The last two can be considered compounds of two compound hexagrams and the last as three compound tetragrams.

• 

  2{6}

• 

  3{4}

• 

  4{3}

• 

  6{2}

Dodecagrams as isotoxal figures

An isotoxal polygon has two vertices and one edge type within its symmetry class. There are 5 isotoxal dodecagram star with a degree of freedom of angles, which alternates vertices at two radii, one simple, 3 compounds, and 1 unicursal star.

Isotoxal dodecagrams

Type	Simple	Compounds			Star
Density	1	2	3	4	5
Image	{(6)α}	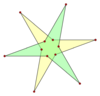2{3α}	3{2α}	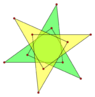2{(3/2)α}	{(6/5)α}

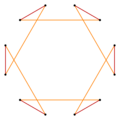
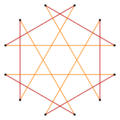
Dodecagrams as isogonal figures

A regular dodecagram can be seen as a quasitruncated hexagon, t{6/5}={12/5}. Other isogonal (vertex-transitive) variations with equally spaced vertices can be constructed with two edge lengths.

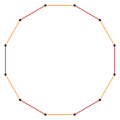t{6}

t{6/5}={12/5}

Complete graph

Superimposing all the dodecagons and dodecagrams on each other – including the degenerate compound of six digons (line segments), {12/6} – produces the complete graph K₁₂.

K₁₂

black: the twelve corner points (nodes) red: {12} regular dodecagon green: {12/2}=2{6} two hexagons blue: {12/3}=3{4} three squares cyan: {12/4}=4{3} four triangles magenta: {12/5} regular dodecagram yellow: {12/6}=6{2} six digons

Regular dodecagrams in polyhedra

Dodecagrams can also be incorporated into uniform polyhedra. Below are the three prismatic uniform polyhedra containing regular dodecagrams (there are no other dodecagram-containing uniform polyhedra).

• 

  Dodecagrammic prism

• 

  Dodecagrammic antiprism

• 

  Dodecagrammic crossed-antiprism

Dodecagrams can also be incorporated into star tessellations of the Euclidean plane.

Dodecagram Symbolism

The twelve-pointed star is a prominent feature on the ancient Vietnamese Dong Son drums

Dodecagrams or twelve-pointed stars have been used as symbols for the following:

• the twelve tribes of Israel, in Judaism
• the twelve disciples, in Christianity
• the twelve olympians, in Hellenic Polytheism
• the twelve signs of the zodiac
• the International Order of Twelve Knights and Daughters of Tabor, an African-American fraternal group
• the fictional secret society Manus Sancti, in the Knights of Manus Sancti series by Bryn Donovan
• The twelve tribes of Nauru on the national flag.

See also

• Stellation
• Star polygon
• List of regular polytopes and compounds

References

• Weisstein, Eric W.. "Dodecagram". http://mathworld.wolfram.com/Dodecagram.html. 
• Grünbaum, B. and G.C. Shephard; Tilings and Patterns, New York: W. H. Freeman & Co., (1987), ISBN:0-7167-1193-1.
• Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993), ed T. Bisztriczky et al., Kluwer Academic (1994) pp. 43–70.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN:978-1-56881-220-5 (Chapter 26. pp. 404: Regular star-polytopes Dimension 2)