Translation surface (differential geometry)
In differential geometry a translation surface is a surface that is generated by translations:
- For two space curves [math]\displaystyle{ c_1, c_2 }[/math] with a common point [math]\displaystyle{ P }[/math], the curve [math]\displaystyle{ c_1 }[/math] is shifted such that point [math]\displaystyle{ P }[/math] is moving on [math]\displaystyle{ c_2 }[/math]. By this procedure curve [math]\displaystyle{ c_1 }[/math] generates a surface: the translation surface.
If both curves are contained in a common plane, the translation surface is planar (part of a plane). This case is generally ignored.
Simple examples:
- Right circular cylinder: [math]\displaystyle{ c_1 }[/math] is a circle (or another cross section) and [math]\displaystyle{ c_2 }[/math] is a line.
- The elliptic paraboloid [math]\displaystyle{ \; z=x^2+y^2\; }[/math] can be generated by [math]\displaystyle{ \ c_1:\; (x,0,x^2)\ }[/math] and [math]\displaystyle{ \ c_2:\;(0,y,y^2)\ }[/math] (both curves are parabolas).
- The hyperbolic paraboloid [math]\displaystyle{ z=x^2-y^2 }[/math] can be generated by [math]\displaystyle{ c_1: (x,0,x^2) }[/math] (parabola) and [math]\displaystyle{ c_2:(0,y,-y^2) }[/math] (downwards open parabola).
Translation surfaces are popular in descriptive geometry[1][2] and architecture,[3] because they can be modelled easily.
In differential geometry minimal surfaces are represented by translation surfaces or as midchord surfaces (s. below).[4]
The translation surfaces as defined here should not be confused with the translation surfaces in complex geometry.
Parametric representation
For two space curves [math]\displaystyle{ \ c_1: \; \vec x=\gamma_1(u)\ }[/math] and [math]\displaystyle{ \ c_2:\; \vec x=\gamma_2(v)\ }[/math] with [math]\displaystyle{ \gamma_1(0)=\gamma_2(0)=\vec 0 }[/math] the translation surface [math]\displaystyle{ \Phi }[/math] can be represented by:[5]
- (TS) [math]\displaystyle{ \quad \vec x=\gamma_1(u)+\gamma_2(v) \; }[/math]
and contains the origin. Obviously this definition is symmetric regarding the curves [math]\displaystyle{ c_1 }[/math] and [math]\displaystyle{ c_2 }[/math]. Therefore, both curves are called generatrices (one: generatrix). Any point [math]\displaystyle{ X }[/math] of the surface is contained in a shifted copy of [math]\displaystyle{ c_1 }[/math] and [math]\displaystyle{ c_2 }[/math] resp.. The tangent plane at [math]\displaystyle{ X }[/math] is generated by the tangentvectors of the generatrices at this point, if these vectors are linearly independent.
If the precondition [math]\displaystyle{ \gamma_1(0)=\gamma_2(0)=\vec 0 }[/math] is not fulfilled, the surface defined by (TS) may not contain the origin and the curves [math]\displaystyle{ c_1,c_2 }[/math]. But in any case the surface contains shifted copies of any of the curves [math]\displaystyle{ c_1,c_2 }[/math] as parametric curves [math]\displaystyle{ \vec x(u_0,v) }[/math] and [math]\displaystyle{ \vec x(u,v_0) }[/math] respectively.
The two curves [math]\displaystyle{ c_1,c_2 }[/math] can be used to generate the so called corresponding midchord surface. Its parametric representation is
- (MCS) [math]\displaystyle{ \quad \vec x=\frac{1}{2}(\gamma_1(u)+\gamma_2(v)) \; . }[/math]
Helicoid as translation surface and midchord surface
A helicoid is a special case of a generalized helicoid and a ruled surface. It is an example of a minimal surface and can be represented as a translation surface.
The helicoid with the parametric representation
- [math]\displaystyle{ \vec x(u,v)= (u\cos v,u\sin v, kv) }[/math]
has a turn around shift (German: Ganghöhe) [math]\displaystyle{ 2\pi k }[/math]. Introducing new parameters [math]\displaystyle{ \alpha, \varphi }[/math][6] such that
- [math]\displaystyle{ u=2a\cos\left(\frac{\alpha-\varphi} 2 \right)\ , \ \ v=\frac{\alpha+\varphi}{2} }[/math]
and [math]\displaystyle{ a }[/math] a positive real number, one gets a new parametric representation
- [math]\displaystyle{ \vec X(\alpha,\varphi)= \left (a\cos\alpha + a\cos \varphi \; ,\; a\sin\alpha + a\sin \varphi\; ,\; \frac{k\alpha}{2}+\frac{k\varphi}{2}\right ) }[/math]
- [math]\displaystyle{ =(a\cos\alpha , a\sin\alpha , \frac{k\alpha}{2} ) \ +\ (a\cos\varphi , a\sin\varphi ,\frac{k\varphi}{2} )\ , }[/math]
which is the parametric representation of a translation surface with the two identical (!) generatrices
- [math]\displaystyle{ c_1: \; \gamma_1=\vec X(\alpha,0)=\left(a+a\cos\alpha , a\sin\alpha , \frac{k\alpha}{2} \right) \quad }[/math] and
- [math]\displaystyle{ c_2: \; \gamma_2=\vec X(0,\varphi)=\left(a+a\cos\varphi , a\sin\varphi ,\frac{k\varphi}{2} \right)\ . }[/math]
The common point used for the diagram is [math]\displaystyle{ P=\vec X(0,0)=(2a,0,0) }[/math]. The (identical) generatrices are helices with the turn around shift [math]\displaystyle{ k\pi\;, }[/math] which lie on the cylinder with the equation [math]\displaystyle{ (x-a)^2+y^2=a^2 }[/math]. Any parametric curve is a shifted copy of the generatrix [math]\displaystyle{ c_1 }[/math] (in diagram: purple) and is contained in the right circular cylinder with radius [math]\displaystyle{ a }[/math], which contains the z-axis.
The new parametric representation represents only such points of the helicoid that are within the cylinder with the equation [math]\displaystyle{ x^2+y^2=4a^2 }[/math].
From the new parametric representation one recognizes, that the helicoid is a midchord surface, too:
- [math]\displaystyle{ \begin{align} \vec X(\alpha,\varphi) & = \left(a\cos\alpha , a\sin\alpha , \frac{k\alpha}{2} \right) \ +\ \left(a\cos\varphi , a\sin\varphi ,\frac{k\varphi}{2} \right) \\[5pt] & =\frac{1}{2}(\delta_1(\alpha) +\delta_2(\varphi))\ ,\quad \end{align} }[/math]
where
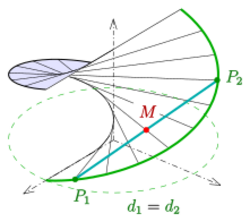
- [math]\displaystyle{ d_1: \ \vec x=\delta_1(\alpha)=(2a\cos\alpha , 2a\sin\alpha , k\alpha ) \ ,\quad }[/math] and
- [math]\displaystyle{ d_2: \ \vec x=\delta_2(\varphi)=(2a\cos\varphi , 2a\sin\varphi , k\varphi ) \ ,\quad }[/math]
are two identical generatrices.
In diagram: [math]\displaystyle{ P_1: \delta_1(\alpha_0) }[/math] lies on the helix [math]\displaystyle{ d_1 }[/math] and [math]\displaystyle{ P_2: \delta_2(\varphi_0) }[/math] on the (identical) helix [math]\displaystyle{ d_2 }[/math]. The midpoint of the chord is [math]\displaystyle{ \ M: \frac{1}{2}(\delta_1(\alpha_0) +\delta_2(\varphi_0))=\vec X(\alpha_0,\varphi_0)\ }[/math].
Advantages of a translation surface
- Architecture
A surface (for example a roof) can be manufactured using a jig for curve [math]\displaystyle{ c_2 }[/math] and several identical jigs of curve [math]\displaystyle{ c_1 }[/math]. The jigs can be designed without any knowledge of mathematics. By positioning the jigs the rules of a translation surface have to be respected only.
- Descriptive geometry
Establishing a parallel projection of a translation surface one 1) has to produce projections of the two generatrices, 2) make a jig of curve [math]\displaystyle{ c_1 }[/math] and 3) draw with help of this jig copies of the curve respecting the rules of a translation surface. The contour of the surface is the envelope of the curves drawn with the jig. This procedure works for orthogonal and oblique projections, but not for central projections.
- Differential geometry
For a translation surface with parametric representation [math]\displaystyle{ \vec x(u,v)=\gamma_1(u)+\gamma_2(v) \; }[/math] the partial derivatives of [math]\displaystyle{ \vec x(u,v) }[/math] are simple derivatives of the curves. Hence the mixed derivatives are always [math]\displaystyle{ 0 }[/math] and the coefficient [math]\displaystyle{ M }[/math] of the second fundamental form is [math]\displaystyle{ 0 }[/math], too. This is an essential facilitation for showing that (for example) a helicoid is a minimal surface.
References
- ↑ H. Brauner: Lehrbuch der Konstruktiven Geometrie, Springer-Verlag, 2013,ISBN:3709187788, 9783709187784, p. 236
- ↑ Fritz Hohenberg: Konstruktive Geometrie in der Technik, Springer-Verlag, 2013, ISBN:3709181488, 9783709181485, p. 208
- ↑ Hans Schober: Transparente Schalen: Form, Topologie, Tragwerk, John Wiley & Sons, 2015, ISBN:343360598X, 9783433605981, S. 74
- ↑ Wilhelm Blaschke, Kurt Reidemeister: Vorlesungen über Differentialgeometrie und geometrische Grundlagen von Einsteins Relativitätstheorie II: Affine Differentialgeometrie, Springer-Verlag, 2013,ISBN:364247392X, 9783642473920, p. 94
- ↑ Erwin Kruppa: Analytische und konstruktive Differentialgeometrie, Springer-Verlag, 2013, ISBN:3709178673, 9783709178676, p. 45
- ↑ J.C.C. Nitsche: Vorlesungen über Minimalflächen, Springer-Verlag, 2013, ISBN:3642656196, 9783642656194, p. 59
- G. Darboux: Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal, 1–4, Chelsea, reprint, 972, pp. Sects. 81–84, 218
- Georg Glaeser: Geometrie und ihre Anwendungen in Kunst, Natur und Technik, Springer-Verlag, 2014, ISBN:364241852X, p. 259
- W. Haack: Elementare Differentialgeometrie, Springer-Verlag, 2013, ISBN:3034869509, p. 140
- C. Leopold: Geometrische Grundlagen der Architekturdarstellung. Kohlhammer Verlag, Stuttgart 2005, ISBN:3-17-018489-X, p. 122
- D.J. Struik: Lectures on classical differential geometry, Dover, reprint ,1988, pp. 103, 109, 184
External links
 |