Tridecahedron
| Common tridecahedrons | |
|---|---|
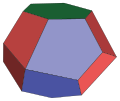 Space-filling tridecahedron |
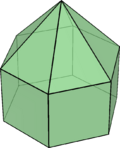 Elongated hexagonal pyramid |
 Hendecagonal prism |
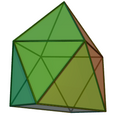 Gyroelongated square pyramid |
A tridecahedron, or triskaidecahedron, is a polyhedron with thirteen faces. There are numerous topologically distinct forms of a tridecahedron, for example the dodecagonal pyramid and hendecagonal prism. However, a tridecahedron cannot be a regular polyhedron, because there is no regular polygon that can form a regular tridecahedron, and there are only five known regular polyhedra.[notes 1][1]
Convex
There are 96,262,938 topologically distinct convex tridecahedra, excluding mirror images, having at least 9 vertices.[2] (Two polyhedra are "topologically distinct" if they have intrinsically different arrangements of faces and vertices, such that it is impossible to distort one into the other simply by changing the lengths of edges or the angles between edges or faces.) There is a pseudo-space-filling tridecahedron that can fill all of 3-space together with its mirror-image.[3]
Common tridecahedrons
Examples
| Name (vertex layout) | Symbol | Stereogram | Expanded view | Faces | Edges | Apexes | |
|---|---|---|---|---|---|---|---|
| Hendecagonal prism | t{2,11} {11}x{} |

|
13 | square × 11 hendecagon × 2 |
33 | 22 | |
| Dodecagonal pyramid | ( )∨{12} | 
|
13 | triangle × 12 dodecagon × 1 |
24 | 13 | |
| Elongated hexagonal pyramid | 
|
13 | triangle × 6 square × 6 hexagon × 1 |
24 | 13 | ||
| Space-filling tridecahedron | 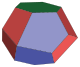
|
|
13 | quadrilateral × 6 pentagon × 6 hexagon × 1 |
30 | 19 | |
| Gyroelongated square pyramid | 
|

|
13 | triangle × 12 square × 1 |
20 | 9 | |
| truncated hexagonal trapohedron | 
|
13 | 1 hexagon base 6 pentagon sides 6 kite sides |
30 | 19 | ||
| Biaugmented pentagonal prism | 
|
|
13 | triangle × 8 square × 3 pentagon × 2 |
23 | 12 | |
Hendecagonal prism
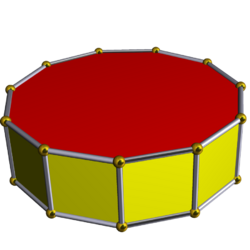
A hendecagonal prism is a prism with a hendecagon base. It is a type of tridecahedron, which consists of 13 faces, 22 vertices, and 33 sides. A regular hendecagonal prism is a hendecagonal prism whose faces are regular hendecagons, and each of its vertices is a common vertex of 2 squares and 1 hendecagon. In a vertex figure a hendecagonal prism is represented by ; in Schläfly notation it can be represented by {11}×{} or t{2, 11}; ![]()
![]()
![]()
![]()
![]()
![]() can be used in a Coxeter-Dynkin diagram to represent it; its Wythoff symbol is 2 11 | 2; in Conway polyhedron notation it can be represented by P11. If the side length of the base of a regular hendecagonal prism is and the height is , then its volume and surface area are:[4]
can be used in a Coxeter-Dynkin diagram to represent it; its Wythoff symbol is 2 11 | 2; in Conway polyhedron notation it can be represented by P11. If the side length of the base of a regular hendecagonal prism is and the height is , then its volume and surface area are:[4]
Dodecagonal pyramid
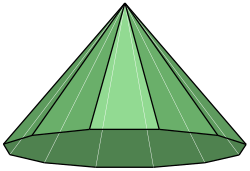
A dodecagonal pyramid is a pyramid with a dodecagonal base. It is a type of tridecahedron, which has 13 faces, 24 edges, and 13 vertices, and its dual polyhedron is itself.[5] A regular dodecagonal pyramid is a dodecagonal pyramid whose base is a regular dodecagon. If the side length of the base of a regular twelve-sided pyramid is and the height is , then its volume and surface area are:[5]
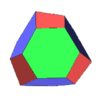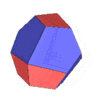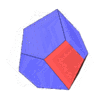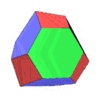
Space-filling tridecahedron
| Space-filling tridecahedron | |
|---|---|
 | |
| Type | 6 trapezoids 6 pentagons 20px 1 regular hexagons |
| Faces | 13 |
| Edges | 30 |
| Vertices | 19 |
A space-filling tridecahedron[6][7] is a tridecahedron that can completely fill three-dimensional space without leaving gaps. It has 13 faces, 30 edges, and 19 vertices. Among the thirteen faces, there are six trapezoids, six pentagons and one regular hexagon.[8]
- Dual polyhedron
The polyhedron's dual polyhedron is an enneadecahedron. It is similar to a twisted half-cube, but one of its vertices is treated as a face before twisting.
| Image | Rotation animation | Expanded view | |
|---|---|---|---|
| Original polyhedron tridecahedron |
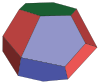
|
|
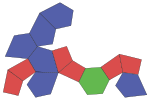
|
| Dual polyhedron enneadecahedron |

|

|

|
Notes
- ↑ Even if there were 13 faces that were all congruent, it would still not be considered a regular polyhedra. In addition to being congruent on each face of a regular polyhedron, the angles and sides on each face must be equal in size. Only regular polygons meet this condition, but the faces of a thirteen-sided shape do not, so there cannot be a regular tridecahedron.
References
- ↑ proof of platonic solids mathsisfun.com [2016-1-10]
- ↑ Counting polyhedra
- ↑ Ludacer, Randy. "Honeycombs and Structural Package Design: More Ways of Taking Up Space". Archived from the original on 2016-03-07. https://web.archive.org/web/20160307203424/http://beachpackagingdesign.com/boxvox/honeycombs-and-structural-package-design-more-ways-of-taking-up-space.
- ↑ Template:WolframAlpha
- ↑ 5.0 5.1 Template:WolframAlpha
- ↑ Oblate Rhombohedra science.unitn.it [2016-1-10]
- ↑ Virtual Polyhedra, Greek Numerical Prefixes , 1996, George W. Hart, georgehart.com [2016-1-10]
- ↑ A space-filling polyhedron with 13 faces science.unitn.it [2016-1-10]
External links
- Self-dual tridecahedra
- What Are Polyhedra?, with Greek Numerical Prefixes
 |
