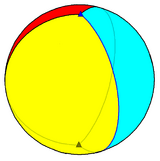
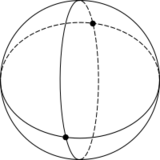
Hosohedron
| Set of regular n-gonal hosohedra | |
|---|---|
 Example regular hexagonal hosohedron on a sphere | |
| Type | regular polyhedron or spherical tiling |
| Faces | n digons |
| Edges | n |
| Vertices | 2 |
| χ | 2 |
| Vertex configuration | 2n |
| Wythoff symbol | n | 2 2 |
| Schläfli symbol | {2,n} |
| Coxeter diagram | |
| Symmetry group | Dnh [2,n] (*22n) order 4n |
| Rotation group | Dn [2,n]+ (22n) order 2n |
| Dual polyhedron | regular n-gonal dihedron |

In spherical geometry, an n-gonal hosohedron is a tessellation of lunes on a spherical surface, such that each lune shares the same two polar opposite vertices.
A regular n-gonal hosohedron has Schläfli symbol {2,n}, with each spherical lune having internal angle 2π/nradians (360/n degrees).[1][2]
Hosohedra as regular polyhedra
For a regular polyhedron whose Schläfli symbol is {m, n}, the number of polygonal faces is :
The Platonic solids known to antiquity are the only integer solutions for m ≥ 3 and n ≥ 3. The restriction m ≥ 3 enforces that the polygonal faces must have at least three sides.
When considering polyhedra as a spherical tiling, this restriction may be relaxed, since digons (2-gons) can be represented as spherical lunes, having non-zero area.
Allowing m = 2 makes
and admits a new infinite class of regular polyhedra, which are the hosohedra. On a spherical surface, the polyhedron {2, n} is represented as n abutting lunes, with interior angles of 2π/n. All these spherical lunes share two common vertices.
Kaleidoscopic symmetry
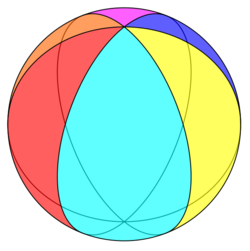
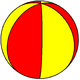
The digonal spherical lune faces of a -hosohedron, , represent the fundamental domains of dihedral symmetry in three dimensions: the cyclic symmetry , , , order . The reflection domains can be shown by alternately colored lunes as mirror images.
Bisecting each lune into two spherical triangles creates an -gonal bipyramid, which represents the dihedral symmetry , order .
| Symmetry (order ) | Schönflies notation | |||||||
|---|---|---|---|---|---|---|---|---|
| Orbifold notation | ||||||||
| Coxeter diagram | ||||||||
| -gonal hosohedron | Schläfli symbol | |||||||
| Alternately colored fundamental domains | 
|
|
|

|

|

| ||
Relationship with the Steinmetz solid
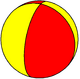
The tetragonal hosohedron is topologically equivalent to the bicylinder Steinmetz solid, the intersection of two cylinders at right-angles.[3]
Derivative polyhedra
The dual of the n-gonal hosohedron {2, n} is the n-gonal dihedron, {n, 2}. The polyhedron {2,2} is self-dual, and is both a hosohedron and a dihedron.
A hosohedron may be modified in the same manner as the other polyhedra to produce a truncated variation. The truncated n-gonal hosohedron is the n-gonal prism.
Apeirogonal hosohedron
In the limit, the hosohedron becomes an apeirogonal hosohedron as a 2-dimensional tessellation:
Hosotopes
Multidimensional analogues in general are called hosotopes. A regular hosotope with Schläfli symbol {2,p,...,q} has two vertices, each with a vertex figure {p,...,q}.
The two-dimensional hosotope, {2}, is a digon.
Etymology
The term “hosohedron” appears to derive from the Greek ὅσος (hosos) “as many”, the idea being that a hosohedron can have “as many faces as desired”.[4] It was introduced by Vito Caravelli in the eighteenth century.[5]
See also
References
- ↑ Coxeter, Regular polytopes, p. 12
- ↑ Abstract Regular polytopes, p. 161
- ↑ Weisstein, Eric W.. "Steinmetz Solid". http://mathworld.wolfram.com/SteinmetzSolid.html.
- ↑ Steven Schwartzman (1 January 1994). The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. MAA. pp. 108–109. ISBN 978-0-88385-511-9. https://archive.org/details/wordsofmathemati0000schw.
- ↑ Coxeter, H.S.M. (1974). Regular Complex Polytopes. London: Cambridge University Press. pp. 20. ISBN 0-521-20125-X. "The hosohedron {2,p} (in a slightly distorted form) was named by Vito Caravelli (1724–1800) …"
- McMullen, Peter; Schulte, Egon (December 2002), Abstract Regular Polytopes (1st ed.), Cambridge University Press, ISBN 0-521-81496-0, https://archive.org/details/abstractregularp0000mcmu
- Coxeter, H.S.M, Regular Polytopes (third edition), Dover Publications Inc., ISBN 0-486-61480-8
External links
 |