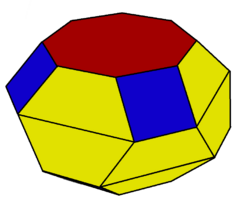
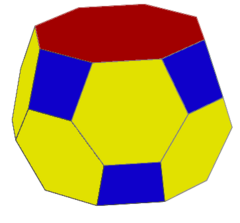
Truncated square antiprism
From HandWiki
| Truncated square antiprism | |
|---|---|
| |
| Type | Truncated antiprism |
| Schläfli symbol | ts{2,8} tsr{4,2} or [math]\displaystyle{ ts\begin{Bmatrix} 4 \\ 2 \end{Bmatrix} }[/math] |
| Conway notation | tA4 |
| Faces | 18: 2 {8}, 8 {6}, 8 {4} |
| Edges | 48 |
| Vertices | 32 |
| Symmetry group | D4d, [2+,8], (2*4), order 16 |
| Rotation group | D4, [2,4]+, (224), order 8 |
| Dual polyhedron | |
| Properties | convex, zonohedron |
The truncated square antiprism one in an infinite series of truncated antiprisms, constructed as a truncated square antiprism. It has 18 faces, 2 octagons, 8 hexagons, and 8 squares.
Gyroelongated triamond square bicupola
If the hexagons are folded, it can be constructed by regular polygons. Or each folded hexagon can be replaced by two triamonds, adding 8 edges (56), and 4 faces (32). This form is called a gyroelongated triamond square bicupola.[1]
Related polyhedra
| Symmetry | D2d, [2+,4], (2*2) | D3d, [2+,6], (2*3) | D4d, [2+,8], (2*4) | D5d, [2+,10], (2*5) |
|---|---|---|---|---|
| Antiprisms |  s{2,4} (v:4; e:8; f:6) |
 s{2,6} (v:6; e:12; f:8) |
 s{2,8} (v:8; e:16; f:10) |
 s{2,10} (v:10; e:20; f:12) |
| Truncated antiprisms |
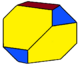 ts{2,4} (v:16;e:24;f:10) |
 ts{2,6} (v:24; e:36; f:14) |
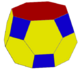 ts{2,8} (v:32; e:48; f:18) |
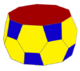 ts{2,10} (v:40; e:60; f:22) |
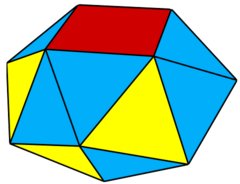
Snub square antiprism
Although it can't be made by all regular planar faces, its alternation is the Johnson solid, the snub square antiprism.
References
 |