Snub square antiprism
| Snub square antiprism | |
|---|---|
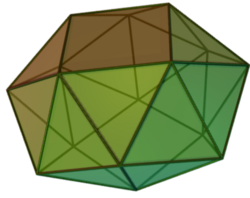 | |
| Type | Johnson J84 – J85 – J86 |
| Faces | 8+16 triangles 2 squares |
| Edges | 40 |
| Vertices | 16 |
| Vertex configuration | 8(35) 8(34.4) |
| Symmetry group | D4d |
| Dual polyhedron | - |
| Properties | convex |
| Net | |
 | |
File:J85 snub square antiprism.stl
In geometry, the snub square antiprism is one of the Johnson solids (J85). A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.[1]
It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids, although it is a relative of the icosahedron that has fourfold symmetry instead of threefold.
Construction
The snub square antiprism is constructed as its name suggests, a square antiprism which is snubbed, and represented as ss{2,8}, with s{2,8} as a square antiprism.[2] It can be constructed in Conway polyhedron notation as sY4 (snub square pyramid).[3]
It can also be constructed as a square gyrobianticupolae, connecting two anticupolae with gyrated orientations.
Cartesian coordinates
Let k ≈ 0.82354 be the positive root of the cubic polynomial
- [math]\displaystyle{ 9x^3+3\sqrt{3}\left(5-\sqrt{2}\right)x^2-3\left(5-2\sqrt{2}\right)x-17\sqrt{3}+7\sqrt{6}. }[/math]
Furthermore, let h ≈ 1.35374 be defined by
- [math]\displaystyle{ h=\frac{\sqrt{2}+8+2\sqrt{3}k-3\left(2+\sqrt{2}\right)k^2}{4\sqrt{3-3k^2}}. }[/math]
Then, Cartesian coordinates of a snub square antiprism with edge length 2 are given by the union of the orbits of the points
- [math]\displaystyle{ (1,1,h),\,\left(1+\sqrt{3}k,0,h-\sqrt{3-3k^2}\right) }[/math]
under the action of the group generated by a rotation around the z-axis by 90° and by a rotation by 180° around a straight line perpendicular to the z-axis and making an angle of 22.5° with the x-axis.[4]
We may then calculate the surface area of a snub square antiprism of edge length a as
- [math]\displaystyle{ A=\left(2+6\sqrt{3}\right)a^2\approx12.39230a^2, }[/math][5]
and its volume as
- [math]\displaystyle{ V=\xi a^3, }[/math]
where ξ ≈ 3.60122 is the greatest real root of the polynomial
- [math]\displaystyle{ 531441x^{12}-85726026x^8-48347280x^6+11588832x^4+4759488x^2-892448. }[/math][6]
Snub antiprisms
Similarly constructed, the ss{2,6} is a snub triangular antiprism (a lower symmetry octahedron), and result as a regular icosahedron. A snub pentagonal antiprism, ss{2,10}, or higher n-antiprisms can be similar constructed, but not as a convex polyhedron with equilateral triangles. The preceding Johnson solid, the snub disphenoid also fits constructionally as ss{2,4}, but one has to retain two degenerate digonal faces (drawn in red) in the digonal antiprism.
| Symmetry | D2d, [2+,4], (2*2) | D3d, [2+,6], (2*3) | D4d, [2+,8], (2*4) | D5d, [2+,10], (2*5) |
|---|---|---|---|---|
| Antiprisms |  s{2,4} A2 (v:4; e:8; f:6) |
 s{2,6} A3 (v:6; e:12; f:8) |
 s{2,8} A4 (v:8; e:16; f:10) |
 s{2,10} A5 (v:10; e:20; f:12) |
| Truncated antiprisms |
 ts{2,4} tA2 (v:16;e:24;f:10) |
 ts{2,6} tA3 (v:24; e:36; f:14) |
 ts{2,8} tA4 (v:32; e:48; f:18) |
 ts{2,10} tA5 (v:40; e:60; f:22) |
| Symmetry | D2, [2,2]+, (222) | D3, [3,2]+, (322) | D4, [4,2]+, (422) | D5, [5,2]+, (522) |
| Snub antiprisms |
J84 | Icosahedron | J85 | Concave |
| sY3 = HtA3 | sY4 = HtA4 | sY5 = HtA5 | ||
 ss{2,4} (v:8; e:20; f:14) |
 ss{2,6} (v:12; e:30; f:20) |
 ss{2,8} (v:16; e:40; f:26) |
ss{2,10} (v:20; e:50; f:32) |
References
- ↑ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics 18: 169–200, doi:10.4153/cjm-1966-021-8.
- ↑ Snub Anti-Prisms
- ↑ "PolyHédronisme". https://levskaya.github.io/polyhedronisme/?recipe=C100sY4.
- ↑ Timofeenko, A. V. (2009). "The non-Platonic and non-Archimedean noncomposite polyhedra". Journal of Mathematical Science 162 (5): 725. doi:10.1007/s10958-009-9655-0.
- ↑ Wolfram Research, Inc. (2020). Wolfram|Alpha Knowledgebase. Champaign, IL. "
PolyhedronData[{"Johnson", 85}, "SurfaceArea"]". - ↑ Wolfram Research, Inc. (2020). Wolfram|Alpha Knowledgebase. Champaign, IL. "
MinimalPolynomial[PolyhedronData[{"Johnson", 85}, "Volume"], x]".
External links
 |

