U-quadratic distribution

U-quadratic

Probability density function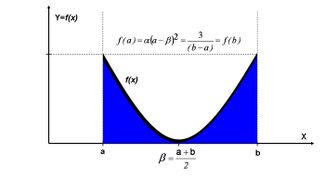
Parameters	[math]\displaystyle{ a:~a \in (-\infty,\infty) }[/math] [math]\displaystyle{ b:~b \in (a, \infty) }[/math] or [math]\displaystyle{ \alpha:~\alpha\in (0,\infty) }[/math] [math]\displaystyle{ \beta:~\beta \in (-\infty,\infty), }[/math]
Support	[math]\displaystyle{ x\in [a , b]\! }[/math]
PDF	[math]\displaystyle{ \alpha \left ( x - \beta \right )^2 }[/math]
CDF	[math]\displaystyle{ {\alpha \over 3} \left ( (x - \beta)^3 + (\beta - a)^3 \right ) }[/math]
Mean	[math]\displaystyle{ {a+b \over 2} }[/math]
Median	[math]\displaystyle{ {a+b \over 2} }[/math]
Mode	[math]\displaystyle{ a\text{ and }b }[/math]
Variance	[math]\displaystyle{ {3 \over 20} (b-a)^2 }[/math]
Skewness	[math]\displaystyle{ 0 }[/math]
Kurtosis	[math]\displaystyle{ {3 \over 112} (b-a)^4 }[/math]
Entropy	TBD
MGF	See text
CF	See text

In probability theory and statistics, the U-quadratic distribution is a continuous probability distribution defined by a unique convex quadratic function with lower limit a and upper limit b.

[math]\displaystyle{ f(x|a,b,\alpha, \beta)=\alpha \left ( x - \beta \right )^2, \quad\text{for } x \in [a , b]. }[/math]

Parameter relations

This distribution has effectively only two parameters a, b, as the other two are explicit functions of the support defined by the former two parameters:

[math]\displaystyle{ \beta = {b+a \over 2} }[/math]

(gravitational balance center, offset), and

[math]\displaystyle{ \alpha = {12 \over \left ( b-a \right )^3} }[/math]

(vertical scale).

Related distributions

One can introduce a vertically inverted ([math]\displaystyle{ \cap }[/math])-quadratic distribution in analogous fashion.

Applications

This distribution is a useful model for symmetric bimodal processes. Other continuous distributions allow more flexibility, in terms of relaxing the symmetry and the quadratic shape of the density function, which are enforced in the U-quadratic distribution – e.g., beta distribution and gamma distribution.

Moment generating function

[math]\displaystyle{ M_X(t) = {-3\left(e^{at}(4+(a^2+2a(-2+b)+b^2)t)- e^{bt} (4 + (-4b + (a+b)^2)t)\right) \over (a-b)^3 t^2 } }[/math]

Characteristic function

[math]\displaystyle{ \phi_X(t) = {3i\left(e^{iate^{ibt}} (4i - (-4b + (a+b)^2)t)\right) \over (a-b)^3 t^2 } }[/math]