Vertical translation
From HandWiki
In geometry, a vertical translation (also known as vertical shift) is a translation of a geometric object in a direction parallel to the vertical axis of the Cartesian coordinate system.[1][2][3]
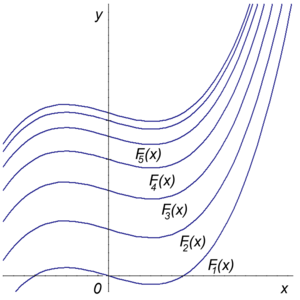
Often, vertical translations are considered for the graph of a function. If f is any function of x, then the graph of the function f(x) + c (whose values are given by adding a constant c to the values of f) may be obtained by a vertical translation of the graph of f(x) by distance c. For this reason the function f(x) + c is sometimes called a vertical translate of f(x).[4] For instance, the antiderivatives of a function all differ from each other by a constant of integration and are therefore vertical translates of each other.[5]
See also
References
- ↑ De Berg, Mark; Cheong, Otfried; Van Kreveld, Marc; Overmars (2008), Computational Geometry Algorithms and Applications, Berlin: Springer, p. 91, doi:10.1007/978-3-540-77974-2, ISBN 978-3-540-77973-5, https://books.google.com/books?id=tkyG8W2163YC&pg=PA91.
- ↑ Smith, James T. (2011), Methods of Geometry, John Wiley & Sons, p. 356, ISBN 9781118031032, https://books.google.com/books?id=B0khWEZmOlwC&pg=PA356.
- ↑ Faulkner, John R. (2014), The Role of Nonassociative Algebra in Projective Geometry, Graduate Studies in Mathematics, 159, American Mathematical Society, p. 13, ISBN 9781470418496, https://books.google.com/books?id=axIBBQAAQBAJ&pg=PA13.
- ↑ Dougherty, Edward R.; Astol, Jaakko (1999), Nonlinear Filters for Image Processing, SPIE/IEEE series on imaging science & engineering, 59, SPIE Press, p. 169, ISBN 9780819430335, https://books.google.com/books?id=4PV-sTF6qJQC&pg=PA169.
- ↑ Zill, Dennis; Wright, Warren S. (2009), Single Variable Calculus: Early Transcendentals, Jones & Bartlett Learning, p. 269, ISBN 9780763749651, https://books.google.com/books?id=0n0iPYKLo74C&pg=PA269.
