Wright Omega function
In mathematics, the Wright omega function or Wright function,[note 1] denoted ω, is defined in terms of the Lambert W function as:
- [math]\displaystyle{ \omega(z) = W_{\big \lceil \frac{\mathrm{Im}(z) - \pi}{2 \pi} \big \rceil}(e^z). }[/math]
Uses
One of the main applications of this function is in the resolution of the equation z = ln(z), as the only solution is given by z = e−ω(π i).
y = ω(z) is the unique solution, when [math]\displaystyle{ z \neq x \pm i \pi }[/math] for x ≤ −1, of the equation y + ln(y) = z. Except on those two rays, the Wright omega function is continuous, even analytic.
Properties
The Wright omega function satisfies the relation [math]\displaystyle{ W_k(z) = \omega(\ln(z) + 2 \pi i k) }[/math].
It also satisfies the differential equation
- [math]\displaystyle{ \frac{d\omega}{dz} = \frac{\omega}{1 + \omega} }[/math]
wherever ω is analytic (as can be seen by performing separation of variables and recovering the equation [math]\displaystyle{ \ln(\omega)+\omega = z }[/math]), and as a consequence its integral can be expressed as:
- [math]\displaystyle{ \int w^n \, dz = \begin{cases} \frac{\omega^{n+1} -1 }{n+1} + \frac{\omega^n}{n} & \mbox{if } n \neq -1, \\ \ln(\omega) - \frac{1}{\omega} & \mbox{if } n = -1. \end{cases} }[/math]
Its Taylor series around the point [math]\displaystyle{ a = \omega_a + \ln(\omega_a) }[/math] takes the form :
- [math]\displaystyle{ \omega(z) = \sum_{n=0}^{+\infty} \frac{q_n(\omega_a)}{(1+\omega_a)^{2n-1}}\frac{(z-a)^n}{n!} }[/math]
where
- [math]\displaystyle{ q_n(w) = \sum_{k=0}^{n-1} \bigg \langle \! \! \bigg \langle \begin{matrix} n+1 \\ k \end{matrix} \bigg \rangle \! \! \bigg \rangle (-1)^k w^{k+1} }[/math]
in which
- [math]\displaystyle{ \bigg \langle \! \! \bigg \langle \begin{matrix} n \\ k \end{matrix} \bigg \rangle \! \! \bigg \rangle }[/math]
is a second-order Eulerian number.
Values
- [math]\displaystyle{ \begin{array}{lll} \omega(0) &= W_0(1) &\approx 0.56714 \\ \omega(1) &= 1 & \\ \omega(-1 \pm i \pi) &= -1 & \\ \omega(-\frac{1}{3} + \ln \left ( \frac{1}{3} \right ) + i \pi ) &= -\frac{1}{3} & \\ \omega(-\frac{1}{3} + \ln \left ( \frac{1}{3} \right ) - i \pi ) &= W_{-1} \left ( -\frac{1}{3} e^{-\frac{1}{3}} \right ) &\approx -2.237147028 \\ \end{array} }[/math]
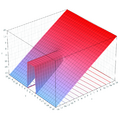
Plots
- Plots of the Wright omega function on the complex plane
z = Re(ω(x + i y))
z = Im(ω(x + i y))
ω(x + i y)
Notes
- ↑ Not to be confused with the Fox–Wright function, also known as Wright function.
References
 |
