x̅ and s chart

[math]\displaystyle{ \bar x }[/math] and s chart
Originally proposed by	Walter A. Shewhart
Process observations
Rational subgroup size	{{{subgroupsize}}}
Measurement type	Average quality characteristic uper unit
Quality characteristic type	Variables data
Underlying distribution	Normal distribution
Performance
Size of shift to detect	≥ 1.5σ
Process variation chart
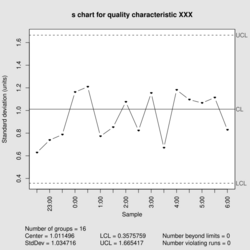Center line	[math]\displaystyle{ \bar s = \frac {\sum_{i=1}^m \sqrt \frac{\sum_{j=1}^n \left ( x_{ij} - \bar {\bar x} \right )^2 }{n - 1}}{m} }[/math]
Upper control limit	[math]\displaystyle{ B_4 \bar S }[/math]
Lower control limit	[math]\displaystyle{ B_3 \bar S }[/math]
Plotted statistic	[math]\displaystyle{ \bar s_i = \sqrt \frac{\sum_{j=1}^n \left ( x_{ij} - \bar x_i \right )^2 }{n - 1} }[/math]
Process mean chart
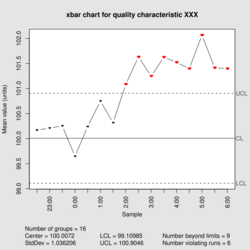Center line	[math]\displaystyle{ \bar x = \frac {\sum_{i=1}^m \sum_{j=1}^n x_{ij}}{mn} }[/math]
Control limits	[math]\displaystyle{ \bar x \pm A_3 \bar s }[/math]
Plotted statistic	[math]\displaystyle{ \bar x_i = \frac {\sum_{j=1}^n x_{ij}}{n} }[/math]

In statistical quality control, the [math]\displaystyle{ \bar x }[/math] and s chart is a type of control chart used to monitor variables data when samples are collected at regular intervals from a business or industrial process. This is connected to traditional statistical quality control (SQC) and statistical process control (SPC). However, Woodall noted that "I believe that the use of control charts and other monitoring methods should be referred to as “statistical process monitoring,” not “statistical process control (SPC).”"

Uses

The chart is advantageous in the following situations:

1. The sample size is relatively large (say, n > 10—[math]\displaystyle{ \bar x }[/math] and R charts are typically used for smaller sample sizes)
2. The sample size is variable
3. Computers can be used to ease the burden of calculation

The "chart" actually consists of a pair of charts: One to monitor the process standard deviation and another to monitor the process mean, as is done with the [math]\displaystyle{ \bar x }[/math] and R and individuals control charts. The [math]\displaystyle{ \bar x }[/math] and s chart plots the mean value for the quality characteristic across all units in the sample, [math]\displaystyle{ \bar x_i }[/math], plus the standard deviation of the quality characteristic across all units in the sample as follows:

[math]\displaystyle{ s = \sqrt{\frac {\sum_{i=1}^n {\left ( x_i - \bar x \right )}^2}{n - 1}} }[/math].

Assumptions

The normal distribution is the basis for the charts and requires the following assumptions:

• The quality characteristic to be monitored is adequately modeled by a normally-distributed random variable
• The parameters μ and σ for the random variable are the same for each unit and each unit is independent of its predecessors or successors
• The inspection procedure is same for each sample and is carried out consistently from sample to sample

Control limits

The control limits for this chart type are:

• [math]\displaystyle{ B_3 \bar s }[/math] (lower) and [math]\displaystyle{ B_4 \bar s }[/math] (upper) for monitoring the process variability
• [math]\displaystyle{ \bar x \pm A_3 \bar s }[/math] for monitoring the process mean

where [math]\displaystyle{ \bar x }[/math] and [math]\displaystyle{ \bar s = \frac {\sum_{i=1}^m s_i}{m} }[/math] are the estimates of the long-term process mean and range established during control-chart setup and A₃, B₃, and B₄ are sample size-specific anti-biasing constants. The anti-biasing constants are typically found in the appendices of textbooks on statistical process control. NIST provides guidance on manually calculating these constants "6.3.2. What are Variables Control Charts?". https://www.itl.nist.gov/div898/handbook/pmc/section3/pmc32.htm#C4. 

Validity

As with the [math]\displaystyle{ \bar x }[/math] and R and individuals control charts, the [math]\displaystyle{ \bar x }[/math] chart is only valid if the within-sample variability is constant. Thus, the s chart is examined before the [math]\displaystyle{ \bar x }[/math] chart; if the s chart indicates the sample variability is in statistical control, then the [math]\displaystyle{ \bar x }[/math] chart is examined to determine if the sample mean is also in statistical control. If on the other hand, the sample variability is not in statistical control, then the entire process is judged to be not in statistical control regardless of what the [math]\displaystyle{ \bar x }[/math] chart indicates.

Unequal samples

When samples collected from the process are of unequal sizes (arising from a mistake in collecting them, for example), there are two approaches:

Technique	Description
Use variable-width control limits	Each observation plots against its own control limits as determined by the sample size-specific values, ni, of A3, B3, and B4
Use control limits based on an average sample size	Control limits are fixed at the modal (or most common) sample size-specific value of A3, B3, and B4

Limitations and improvements

Effect of estimation of parameters plays a major role. Also a change in variance affects the performance of [math]\displaystyle{ \bar{X} }[/math]chart while a shift in mean affects the performance of the S chart.

Therefore, several authors recommend using a single chart that can simultaneously monitor [math]\displaystyle{ \bar{X} }[/math]and S. McCracken, Chackrabori and Mukherjee developed one of the most modern and efficient approach for jointly monitoring the Gaussian process parameters, using a set of reference sample in absence of any knowledge of true process parameters.

See also

• [math]\displaystyle{ \bar x }[/math] and R chart
• Shewhart individuals control chart
• Simultaneous monitoring of mean and variance of Gaussian Processes with estimated parameters (when standards are unknown)